HMM隐马尔科夫算法(Hidden Markov Algorithm)初探

1. HMM背景

0x1：概率模型 - 用概率分布的方式抽象事物的规律

机器学习最重要的任务，是根据一些已观察到的证据（例如训练样本）来对感兴趣的未知变量（例如类别标记）进行估计和推测。

概率模型（probabilistic model）提供了一种描述框架，将学习任务归结于计算未知变量的概率分布，而不是直接得到一个确定性的结果。

在概率模型中，利用已知变量推测未知变量的分布称为“推断（inference）”，其核心是如何基于可观测变量推测出未知变量的条件分布。

具体来说，假定所关心的变量集合为 Y，可观测变量集合为 O，其他变量的集合为 R。

生成式模型（generative model）考虑联合分布 P（Y，R，O）；

判别式模型（discriminative model）考虑条件分布 P（Y，R | O）；

给定一组观测变量值，推断就是要由 P（Y，R，O）或 P（Y，R | O）得到条件概率 P（Y | O）。

直接利用概率求和规则消去变量 R 显然不可行，因为即使每个变量仅有两种取值的简单问题，其复杂度已至少是。另一方面，属性变量之间往往存在复杂的联系，因此概率模型的学习，即基于训练样本来估计变量分布的参数往往相当困难。

为了便于研究高效的推断和学习算法，需要有一套能够简洁紧凑地表达变量间关系的工具。

0x2：概率图模型（probabilistic graphical model）

概率图模型是一类用图来表达变量相关关系的概率模型。它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”。

根据边的性质不同，概率图模型可大致分为两类：

1. 使用有向无环图表示变量间依赖关系：有向图模型或贝叶斯网（Bayesian network）；
2. 使用无向图表示变量间的相关关秀：无向图模型或马尔科夫网（Markov network）；

0x3：隐马尔科夫模型

隐马尔科夫模型（Hiden Markov Model HMM）是结构最简单的动态贝叶斯网（dynamic Bayesian network），这是一种著名的有向图模型，在时序数据建模上比较适用。

0x4: 马尔科夫模型适用的场景 - 处理顺序数据

我们知道，在进行贝叶斯估计、SVM等分类的时候，我们常常基于一个大前提假设：数据集里的数据是独立同分布的。这个假设使得我们将似然函数表示为在每个数据点处计算的概率分布在所有数据点上的乘积。但是在实际应用中，还大量存在另一种场景是独立同分布不成立的，典型的如顺序数据的数据集，这些数据通常产生于沿着时间序列进行的测量（即带时序特征的样本），例如某个特定地区的连续若干天的降水量测量，或者每天汇率的值，或者对于语音识别任务在连续的时间框架下的声学特征，或者一个英语句子中的字符序列。

需要注意的是：时序只是顺序数据的一个特例，马尔科夫模型适用于所有形式的顺序数据

0x5：笔者对隐马尔科夫中“隐序列”的思考

HMM的核心思想认为，任何在现实世界观测到的现象，其背后一定有一个“本质规律”在支撑这一事实，“本质规律”衍生出被我们观测到的现象。

其实隐状态序列只是我们的一个副产品，HMM训练最重要的事情是推断概率转移矩阵以及发射矩阵。

和RNN类似，观测序列之间不存在依赖，而是在隐状态序列之间存在依赖，区别在于HMM中这种依赖是有限的（N阶），而RNN中这种依赖是一直递归到初始状态的（虽然实际上梯度不可能传递到初始状态）

通过HMM进行解码问题（例如语音翻译），即根据观测序列提取隐状态序列的这种思想，和将DNN中隐藏层作为输入向量的抽象特征的思想很类似。

Relevant Link:

《机器学习》周志华

 

2. 从一个虚构的例子引入马尔科夫模型讨论

在开始讨论HMM的数学公式以及计算方法之前，我们先来讨论一个很有趣的例子。在这里例子中，笔者并不会完全遵从HMM的专业术语，而是采用最符合“直觉”的描述语言。虽然可能定义并不准确，但是希望向读者朋友传递一个推导和理解的思想，我们的HMM为什么会被创造出来，以及HMM具体解决了什么问题。

0x1: 实验例子说明

掷骰子。假设我手里有三个不同的骰子

1. 第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6
2. 第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4
3. 第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8

我们构造的场景就是掷骰子实验。

1.实验假设前提

1. 每次从三个骰子里挑一个，挑到每一个骰子的概率未知；
2. 每次选的骰子对下一次选择是否有影响也是未知；
3. 对每个骰子来说抛到某一个面的概率是相等的（即骰子是没有动过手脚的）

2. 实验结果数据采集

我们不断重复掷骰子，每次得到一个数字，不停的重复该过程，我们会得到一串数字

经过10次实验，我们得到一串数字：1 6 3 5 2 7 3 5 2 4

3. 实验目标

得到观测结果后，我们的目标是进行一些列概率估计：

1. 我们得到了这一串数字，每次抛骰子具体是3个中的哪个骰子是未知的，现在需要估计出整个10次实验中最可能的骰子类型是什么（即每次实验对应的骰子）；
2. 我们得到了这一串数字，每次抛骰子具体是3个中的哪个骰子是未知的，现在需要估计出现这个观测结果（这一串数字）的概率有多大

这2个问题非常具有代表性，它们实际上代表了HMM问题中的解码和预测两类核心问题。我们来稍微深入一些讨论这个问题。

0x2: 从独立同分布假设开始 - 极简化的HMM假设

写这章的目的是为了能更好的阐述HMM的序列依赖假设，对HMM熟悉的读者可能会挑战说，HMM至少是1阶的，即至少存在“一步依赖”关系。没错！！

笔者在这里作的独立同部分假设，本质上可以理解为是0阶HMM假设，读者朋友在阅读完这章后，可以对比下独立同部分假设和N阶序列依赖假设在对时序数据进行模式提取的时候的不同变现，从而在实际项目中选择是否需要应用HMM去解决你的实际问题。

1. 独立同分布假设

对上面的问题，我们先建立一个基本假设：

1. 每次实验选择什么骰子是完全独立随机的（即 1/3）；
2. 每次实验和上一次实验也不存在关系，即实验之间是独立同分布的；

有了这个基本假设，我们现在可以开始进行最大似然估计（你当然也可以进行极大后验估计，我们在这里不增加讨论的复杂度）

2. 我们得到了这一串数字，每次抛骰子具体是3个中的哪个骰子是未知的，现在需要估计出整个10次实验中最可能的骰子类型是什么（即每次实验对应的骰子）

以第一轮实验说明问题，我们写出概率表达式：P（S骰子= Sx，Res结果=1 | Model）

P（S骰子= S1，Res结果=1 | Model） = 1 / 6

P（S骰子= S2，Res结果=1 | Model） = 1 / 4

P（S骰子= S3，Res结果=1 | Model） = 1 / 8

这个场景很简单，求最大似然的解不需要求导即可得是 P（S骰子= S2，Res结果=1 | Model），即第一轮最有可能的骰子类型是2号骰子

同理根据最大似然估计原理可得全部10次实验的骰子类型序列：

Res：1，S = S2
Res：6，S = S1
Res：3，S = S2
Res：5，S = S1
Res：2，S = S2
Res：7，S = S3
Res：3，S = S2
Res：5，S = S1
Res：2，S = S2
Res：4，S = S2

插一句题外话，再仔细观察下数据，会发现Res在【1，4】范围中，最大似然结果都是S2，Res在【5，6】范围中，最大似然结果都是【S1，S2】范围中，而Rest在【7，8】，最大似然结果都是【S3】范围中。这表明我们可以训练一个决策树模型去建立一个分类器，并且一定能得到较好的效果。

3. 我们得到了这一串数字，每次抛骰子具体是3个中的哪个骰子是未知的，现在需要估计出现这个观测结果（这一串数字序列）的概率有多大

还是在独立同分布假设下，根据概率分布加法原理，我们可得每次实验出现指定结果的概率：

P（Res结果=1 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=1 | Model）+ P（S骰子= S3，Res结果=1 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24
P（Res结果=6 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=6 | Model）+ P（S骰子= S3，Res结果=6 | Model） = 1 / 6 + 0 + 1 / 8 = 7 / 24
P（Res结果=3 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=3 | Model）+ P（S骰子= S3，Res结果=3 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24
P（Res结果=5 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=5 | Model）+ P（S骰子= S3，Res结果=5 | Model） = 1 / 6 + 0 + 1 / 8 = 7 / 24
P（Res结果=2 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=2 | Model）+ P（S骰子= S3，Res结果=2 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24
P（Res结果=7 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=7 | Model）+ P（S骰子= S3，Res结果=7 | Model） = 0 + 0 + 1 / 8 = 1 / 8
P（Res结果=3 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=3 | Model）+ P（S骰子= S3，Res结果=3 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24
P（Res结果=5 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=5 | Model）+ P（S骰子= S3，Res结果=5 | Model） = 1 / 6 + 0 + 1 / 8 = 7 / 24
P（Res结果=2 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=2 | Model）+ P（S骰子= S3，Res结果=2 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24
P（Res结果=4 | Model） = P（S骰子= S1，Res结果=1 | Model） + P（S骰子= S2，Res结果=4 | Model）+ P（S骰子= S3，Res结果=4 | Model） = 1 / 6 + 1 / 4 + 1 / 8 = 13 / 24

最后，求10次实验的联合概率即为出现指定观测序列的概率：

(13 / 24) * (7/24) *  (13 / 24) * (7/24) * (13 / 24) * (1/8) * (13 / 24) * (7/24) * (13 / 24) * (13 / 24) = 7.83363029759e-05

0x3: 马尔科夫假设

现在把问题放到马尔科夫的理论框架下讨论。

1. N阶序列依赖假设

好，现在我们修改假设前提：

1. 从一次实验到下一次选择什么骰子是完全随机的（即 1/3 ），也即状态转移概率为 1/3；
2. 每次实验之前不再是独立同分布的，每次实验都与之前的N次实验有依赖关联；

这个假设就是N阶序列依赖性假设，每次掷的骰子取决于之前几次掷的骰子，即掷骰子实验之间存在转换概率。

2. 观测序列

在实验观测中，得到的一串数字：1 6 3 5 2 7 3 5 2 4 叫做可见状态链，也即观测序列。

3. 隐藏状态序列

在HMM马尔科夫假设中，每次实验之间并不是独立同分布的而是存在时序依赖关系，但是实际问题中我们永远不知道实际的隐含状态链，因为极大似然估计的也不一定就是真实的情况）。

4. 隐藏状态转移矩阵

这导致掷骰子之间的转换概率（transition probability）分布是未知的（这等价于EM算法中的隐变量是未知的）

5. 输出概率矩阵

同样的，尽管可见状态之间没有转换概率，但是隐含状态向可见状态之间有一个概率叫做输出概率（emission probability）。

就我们的例子来说：

六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6；
四面骰（D4）产生1的输出概率是1/4。产生2，3，4的概率也都是1/4；
八面骰（D8）产生1的输出概率是1/8。产生2，3，4，5，6，7，8的概率也都是1/8；

6. 我们得到了这一串数字（可见状态链已知），现在需要估计出整个10次实验中最可能的骰子类型是什么（即求隐状态序列）

在实验观测中，得到的一串数字：1 6 3 5 2 7 3 5 2 4。现在要在马尔科夫假设的前提下求每次实验最可能的筛子序列。

这本质上是在根据实现结果（可见状态链），求隐藏状态序列时序的最大似然估计。很显然，因为实验之间不再独立同分布了，我们无法像上面那样逐个计算了。

表面上看，其实最简单而暴力的方法就是穷举所有可能的骰子序列，然后把每个序列对应的概率算出来（像前面的算式那样）。然后我们从里面把对应最大概率的序列挑出来就行了。

但是要注意的每次掷骰子实验之间并不是独立同分布的，所以所有序列要计算的次数是：1 + 2! + 3! + ... + 序列Length！，如果马尔可夫链不长，当然可行。如果长的话，穷举的数量太大，就很难完成了。

另外一种很有名的算法叫做Viterbi algorithm. 要理解这个算法，算法的数学公式和推导我们在本章的后面会讨论，这里我们用简单的描述先来尝试理解它的思想：局部最优递推思想。

首先，如果我们只掷一次骰子：

实验观测结果为1，根据最大似然原理对应的最大概率骰子序列就是D4，因为D4产生1的概率是1/4，高于1/6和1/8，所以P1（D4） = 1 / 3

以P1（D4）作为起点，把这个情况拓展（递推），我们掷两次骰子：

实验结果为1，6，我们计算三个值，分别是第二个骰子是D6，D4，D8的最大概率。

根据最大似然原理，第二个骰子应该是D6，第二个骰子取到D6的最大概率是：
（复用了第一步的结果）
同样的，我们可以计算第二个骰子是D4或D8时的最大概率。我们发现，第二个骰子取到D6的概率最大。

而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。

继续拓展，我们掷三次骰子：

同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概率，第二个骰子必须为D6（注意，当转移概率不是1/3等分的时候，当前步的前次依赖不一定是上一次的计算结果，也可能是其他值）。

这时，第三个骰子取到D4的最大概率是
同上，我们可以计算第三个骰子是D6或D8时的最大概率。我们发现，第三个骰子取到D4的概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序列就是D4 D6 D4。

可以看到，掷多少次都可以以此类推。最后得到最有可能的筛子序列。

我们发现，我们要求最大概率骰子序列时要做这么几件事情

1. 首先，不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率；

2. 然后，逐渐增加长度，每增加一次长度，重新算一遍N步长度前到这个长度下最后一个位置取到每个骰子的最大概率（如果是1阶HMM只要算上一步即可），
注意，不是说直接把上一步结果拿过来直接用就可以了，在转移概率不是等比随机的情况下，上一步不是概率最大的路径可能在这一步变为最大。
但是好消息是，N步长度前到这个长度长度下的取到每个骰子的最大概率都算过了，计算过程中只要保存下来重新算并不难。
按照这个方法，当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。

3. 最后，我们把对应这个最大概率的序列从后往前推出来，就得到最大概率骰子序列

7. 我们得到了这一串数字（可见状态链已知），现在需要估计状态转移矩阵以及输出概率矩阵（即估计模型参数）

换言之，什么样的模型能最好地描述这个观测数据，

8. 我们得到了这一串数字（可见状态链已知），每次抛骰子类型已知（转换概率已知），现在需要估计出现这个观测结果的概率有多大

其实本质上这相当于隐变量已知，则问题就退化为一个普通的概率求解问题，解决这个问题的算法叫做前向算法（forward algorithm）。

隐状态链以及观测结果序列如下：

同时假设一个转换概率：

1. D6的下一个状态是D4，D6，D8的概率都是1/3
2. D4的下一个状态是D4，D6，D8的概率都是1/3
3. D8的下一个状态是D4，D6，D8的概率都是1/3

则出现该观测结果的概率计算公式为：

P =

P（D6） * P（D6 -> 1） *

P（D6 -> D8）* P（D8 -> 6） *

P（D8 -> D8）* P（D8 -> 3） *

P（D8 -> D6）* P（D6 -> 5） *

P（D6 -> D4）* P（D4 -> 2） *

P（D4 -> D8）* P（D8 -> 7） *

P（D8 -> D6）* P（D6 -> 3） *

P（D6 -> D6）* P（D6 -> 5） *

P（D6 -> D4）* P（D4 -> 2） *

P（D4 -> D8）* P（D8 -> 4） =

1 / 3 * 1 / 6 * 1 / 3 * 1 / 8 * 1 / 3 * 1 / 8 * 1 / 3 * 1 / 6 * 1 / 3 * 1 / 4 * 1 / 3 * 1 / 8* 1 / 3 * 1 / 6 * 1 / 3 * 1 / 6 * 1 / 3 * 1 / 4 * 1 / 3 * 1 / 8 = 1.99389608506e-13

可以看到，HMM衍生于EM，但是又在EM的基础上增加了一些特性，例如

1. 在HMM中，隐变量是转换概率。知道了转换概率，根据实验观测结果可以最大似然推测出时序
2. HMM中，隐变量和观测变量的关系是前者决定后者的关系，即输出概率

Relevant Link:

http://blog.163.com/zhoulili1987619@126/blog/static/353082012013113191924334/ 
https://www.zhihu.com/question/20962240

 

3. 马尔科夫模型介绍

0x1：隐马尔可夫模型图结构

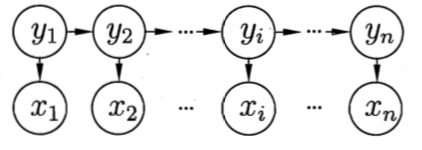
如上图所示，隐马尔科夫模型中的变量可分为两组：

第一组：状态变量，其中表示第 i 时刻的系统状态。通常假定状态变量是隐藏的、不可被观测的，因此状态变量也被称为隐变量（hidden variable）

第二组：观测变量，其中表示第 i 时刻的观测值。

在隐马尔可夫模型中，系统通常在多个状态之间转换，因此状态变量的取值范围 Y（状态空间）通常是有 N 个可能取值的离散空间。

图中的箭头表示了变量间的依赖关系，它是一种动态贝叶斯网。

在任一时刻，观测变量的取值仅依赖于状态变量，即由确定，与其他状态变量及观测变量的取值无关。这是由HMM的概率图结构决定的。

当然，读者在研究RNN及其相关扩展的时候，会看到大量其他的变种模型，变量之间的依赖会变得非常的复杂同时也带来新的能力。但是对于HMM，我们要牢记上面这个概率图模型，HMM规定了这种概率图模型，这也限定了HMM能够具备的能力以及解决问题的范围。

同时，在 N 阶马尔科夫模型中，t 时刻的隐状态仅依赖于 t - N 时刻的状态 Yt-n，与其余状态无关。这就是所谓的“马尔柯夫链（Markov chain）”。

0x2: 马尔科夫假设 - 序列依赖

这个小节我们来讨论下马尔科夫假设，它是什么？为什么要这么假设？这种假设的合理性在哪里？

1. 对含有序列特征的数据集建立独立同分布假设不合理

为了理解马尔科夫假设，我们先从独立同分布假设开始（朴素贝叶斯中采用了独立同分布假设）。

毫无疑问，处理序列数据的最简单的方式是忽略数据集中的序列性质，而将所有观测看作是独立同分布

但是这种方法缺点就是无法利用数据中的序列模式（在很多场景下这种假设都是不成立的）

2. 考虑当前状态和所有历史状态的依赖关系 - 一种极端的假设

我们来对假设进行一些改进，我们假设：每一个当前状态都与此之前的所有状态存在依赖关系，即今天是否下雨其实是由今天之前的整个慢慢历史长河（从宇宙爆发开始）的所有日子是否下雨的结果而决定的（因果论），即：

从某种程度上来说，这种假设没有问题，理论上它是成立的，但问题在于计算量太过巨大，而且实际上距离太过久远之前的序列对当前序列的影响实际上是微乎其微的。

我们为了预测明天的天气，要把地球形成之初到昨天所有的天气情况都输入模型进行训练，这种计算量是不可接受的。

3. 一阶马尔科夫假设 - 只考虑相邻上一步的序列依赖关系

为了缓解独立同分布和完整历史序列依赖的缺点，马尔科夫假设建立了一个近似逼近，对上面的联合概率分布，进行一个改进：

我们现在假设右侧的每个条件概率分布只与最近的⼀次观测有关，⽽独⽴于其他所有之前的观测，那么我们就得到了⼀阶马尔科夫链（first-order Markov chain）

从定义可知，一阶隐马尔可夫链作了两个基本假设：

1）齐次马尔科夫性假设

假设隐藏的马尔柯夫链（隐状态序列）在任意时刻 t 的状态只依赖于前一时刻的状态，与其他时刻的状态及观测无关，也与当前时刻 t 无关：

2）观测独立性假设

假设任意时刻的观测只依赖于该时刻的马尔柯夫链的状态（观测与隐状态一一对应），与其他观测及状态无关：

0x3: 隐马尔可夫模型的定义

隐马尔可夫模型是关于时序的概率模型。

1. 模型结构信息

一阶马尔科夫模型的结构如下：

2. 状态转移概率

模型在各个状态间转换的概率，通常记为矩阵 A = ，其中 N 是所有可能的状态数，

表示在任意时刻 t，若状态为，则在下一时刻状态为的概率。

3. 输出观测概率

模型根据当前状态获得各个观测值的概率，通常记为矩阵，其中 M 是所有可能的观测的类型数。

表示在任意时刻 t，若状态为，则观测值被获取的概率。

4. 初始状态概率

模型在初始时刻各状态出现的概率，通常记为 = ，其中

表示模型的初始状态（t = 1）为的概率。

确定上述参数，就能确定一个隐马尔可夫模型。

隐马尔可夫模型由初始状态概率向量、状态转移概率矩阵A、和观测概率矩阵B决定。

和A决定状态序列；B决定观测序列。

因此，隐马尔可夫模型可以用三元符号表示，即：，A，B，称为隐马尔可夫模型的三要素。

0x4: 隐马尔可夫模型的3个基本问题

理解隐马尔可夫模型的3个基本问题笔者认为非常重要，这3个问题是对现实世界实际问题的数学抽象。

1. 观测序列概率计算 - 评估模型与观测序列之前的匹配程度

给定模型和观测序列，计算在模型下观测序列 O 出现的概率。

这个问题场景也常使用维特比算法（Viterbi algorithm）、前向后向算法（Forward-Backward algorithm）这类递推算法来完成概率似然计算。

这个场景是异常检测中最常见的形式，通常我们根据一组训练样本训练得到一个HMM模型，之后需要根据这个模型预测未来的未知观测序列，根据概率计算结果评估这些新序列的异常程度。

这类问题还有另一个常用的场景，根据以往的观测序列来推测当前时刻最有可能的观测值，显然可以通过softmax来确定概率最大的下一步序列。

2. 学习问题 - 模型训练

已知观测序列，估计模型的参数，使得在该模型下观测序列概率最大，即用极大似然估计的方法估计参数。

在大多数现实应用中，人工指定模型参数已变得越来越不可行。

对这类问题的求解，需要使用EM算法来完成在存在隐变量条件下的最大似然估计，例如Baum-Welch algorithm。

3. 预测问题/解码问题 - 反推隐藏状态序列

已知模型和观测序列，求对给定观测序列条件概率最大的隐状态序列。

即给定观测序列，求最有可能的对应的隐状态序列。

这常见于语言翻译，语言解码翻译等问题（从待翻译语言的空间映射到目标语言的空间中）。

值得注意的是，HMM的隐状态序列的最大似然估计和传统的统计概率最大似然估计不同在于HMM中状态之间还要考虑前序状态的依赖，即当前的状态和前面N（N阶马尔科夫模型）个状态还存在一定的转移概率关系，这使得HMM的最大似然估计不能简答的进行计数统计分析，而需要利用维特比算法（Viterbi algorithm）、前向后向算法（Forward-Backward algorithm）这类递推算法来完成序列最大似然估计。

Relevant Link:

https://www.zhihu.com/question/20962240
http://www.cnblogs.com/skyme/p/4651331.html
http://blog.csdn.net/bi_mang/article/details/52289087
https://yanyiwu.com/work/2014/04/07/hmm-segment-xiangjie.html
https://www.zhihu.com/question/20962240
https://www.zhihu.com/question/52778636
https://www.zhihu.com/question/37391215
https://www.zhihu.com/question/20551866
https://www.zhihu.com/question/28311766
https://www.zhihu.com/question/28311766
https://www.zhihu.com/question/22181185

 

4. 观测序列概率计算算法 - 马尔科夫模型中的观测序列概率计算

概率计算算法的目标是给定模型和观测序列，计算在模型下观测序列 O 出现的概率。

0x1: 直接计算法

给定模型和观测序列，计算观测序列 O 出现的概率，最直接的方法是按照概率公式直接计算，通过枚举所有可能的长度为 T 的状态序列，并求各个状态序列 I 与观测序列的联合概率，然后对所有可能的状态序列求和，得到

状态序列的概率是：

对固定的状态序列，观测序列的概率是，

O 和 I 同时出现的联合概率为：

然后，对所有可能的状态序列 I 求和，得到观测序列 O 的概率，即

但是，该公式的计算量很大，是阶的，这种算法在实际应用中不可行，取而代之的是接下来要讨论的前向-后向算法（forward-backward algorithm）。

0x2: 前向-后向算法

1. 前向算法 - 一种递归算法

首先定义前向概率，给定隐马尔可夫模型，定义到时刻 t 部分观测序列为，且当前时刻状态为的概率为前向概率，记作：

可以递推地求得所有时刻的前向概率及观测序列概率。算法过程如下

（1）初值：，是初始时刻的状态和观测的联合概率

 

（2）递推：对，有：，乘积就是时刻 t 观测到并在时刻 t 处于状态而在时刻 t + 1 到达状态 的联合概率。对这个乘积在时刻 t 的所有可能的 N 个状态求累加和，其结果就是到时刻 t 观测为并在时刻 t + 1处于状态的联合概率

（3）终止：

可以看到，前向算法实际是基于“状态序列的路径结构”递推计算。前向算法高效的关键是其局部计算前向概率，然后利用路径结构将前向概率“递推”到全局。得到。
具体地，在各个时刻，计算的N个值（i = 1，2，...，N），而且每个的计算都要利用前一时刻N的。

减少计算量的原因在于每一次计算直接引用前一时刻的计算结果，避免重复计算。这样，利用前向概率计算的计算量是阶，而不是直接计算的阶

前向算法是一种计算优化算法，本质是把中间计算结果缓存的直接概率计算法。

2. 前向算法的一个具体应用举例

考虑盒子和球模型

状态的集合是：

球的颜色对应观测，观测的集合是：

状态序列和观测序列长度 T = 3

初始概率分布为：

状态转移概率矩阵为：

观测概率矩阵为：

观测序列集合V为：O = ｛红，白，红｝

现在要计算的问题是：出现该观测序列的最大似然概率是多少？

1）计算初值

在第一轮初始值的计算中，所有状态都没有t-1状态，只有初始状态自己。

a1（1） = π1 * b1（o1）= 0.2 * 0.5 = 0.1

a1（2） = π2 * b2（o1）= 0.4 * 0.4 = 0.16

a1（3） = π3 * b3（o1）= 0.4 * 0.7 = 0.28

2）递推计算 t = 2

从t=2开始，计算每个状态的概率都要累加上一轮所有其他状态转移到该状态的概率和。

= （a1（1） * a11 + a1（2） * a21 + a1（3） * a31） * b1（o2） = （0.1 * 0.5 + 0.16 * 0.3 + 0.28 * 0.2）* 0.5 = 0.077

= （a1（1） * a12 + a1（2） * a22 + a1（3） * a32） * b2（o2） = （0.1 * 0.2 + 0.16 * 0.5 + 0.28 * 0.3）* 0.6 = 0.184 * 0.6 = 0.1104

= （a1（1） * a13 + a1（2） * a23 + a1（3） * a33） * b3（o2） = （0.1 * 0.3 + 0.16 * 0.2 + 0.28 * 0.5）* 0.3 = 0.202 * 0.3 = 0.0606

3）递推计算 t = 3

= （a2（1） * a11 + a2（2） * a21 + a2（3） * a31） * b1（o3） = （0.077 * 0.5 + 0.1104 * 0.3 + 0.0606* 0.2）* 0.5 = 0.04187

= （a2（1） * a12 + a2（2） * a22 + a2（3） * a32） * b1（o3） = （0.077 * 0.2 + 0.1104 * 0.5 + 0.0606* 0.3）* 0.4 = 0.035512

= （a2（1） * a13 + a2（2） * a23 + a2（3） * a33） * b1（o3） = （0.077 * 0.3 + 0.1104 * 0.2 + 0.0606* 0.5）* 0.7 = 0.052836

可以看到，t = 3的时刻复用了 t = 2的结果。

4）终止

= a3（1） + a3（2）+ a3（3） = 0.04187 + 0.035512 + 0.052836 = 0.130218

最后一步终止只要对对T-1时刻的结果进行累加即可。条件概率可以通过边缘概率累加计算得到。

3. 后向算法 - 一种递推算法

先来定义后向概率，给定隐马尔可夫模型，定义在时刻 t 状态为的条件下，从 t + 1 到 T 的部分观测序列为的概率为后向概率，记作：，可以用递推的方法求得后向概率及观测序列概率。算法流程如下

（1）初始化后向概率：，对最终时刻的所有状态规定

（2）后向概率的递推公式：，为了计算在时刻 t 状态为条件下时刻 t + 1之后的观测序列为的后向概率，只需考虑在时刻 t + 1所有可能的N个状态的转移概率（即项），以及在此状态下的观测的观测概率（即项），然后考虑状态之后的观测序列的后向概率（即项）（递推下去）

 （3）最终结果：，可以看到后向概率的最终结果表达式就是前向概率的初始化表达式

笔者思考：后向算法就是前向算法的递归倒推的改写，很像C语言中的for循环和递归的关系，核心原理都是逐步递推循环。

前向概率和后向概率可以统一起来，利用前向概率和后向概率的定义可以将观测序列概率统一写成：

Relevant Link:

《统计机器学习》李航

 

5. 隐马尔柯夫模型学习算法 - 模型参数最大似然估计

0x1: 监督学习方法

如果训练数据包括观测序列和对应的状态序列，则可以使用监督学习方法进行隐马尔可夫模型的训练学习。

假设训练数据包含 S 个长度相同的观测序列和对应的状态序列，那么可以利用极大似然估计法来估计隐马尔科夫模型的参数，具体流程如下

1. 转移概率矩阵的估计

设样本中时刻 t 处于状态 i，时刻 t + 1 转移到状态 j 的频数为，那么状态转移概率的最大似然估计公式是：

2. 观测概率矩阵的估计

设样本中状态为 j 并观测为 k 的频数是，那么状态为 j 观测为 k 的概率的最大似然估计是：

3. 初始状态概率的估计

为 S 个样本中初始状态为的频率

可以看到，最大似然估计本质上就是最简单的频数统计法，但是在实际项目中，大多数时候我们是拿不到隐状态序列。所以接下来要讨论的是无监督下的模型参数训练。

0x2: 无监督学习方法 - Baum-Welch算法（EM算法）

假设给定训练数据只包含 S 个长度为 T 的观测序列，而没有对应的状态序列（即包含隐变量），目标是学习隐马尔可夫模型的参数。

套用EM算法的框架，我们将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据 I，那么隐马尔可夫模型实际上是一个含有隐变量的概率模型：

模型参数的学习可以通过EM算法实现。

1. 确定完全数据的对数似然函数

所有观测数据写成，所有隐数据写成，完整的联合概率分布是，完全数据的对数似然函数是：

2. EM算法的 E 步：

求 Q 函数 ，其中，是隐马尔可夫模型参数的本轮次当前估计值，是要极大化的隐马尔可夫模型参数

又因为，

所以 Q 函数可以写成：，

式中所有求和都是对所有训练数据的序列总长度 T 进行的。

3. EM算法的 M 步

极大化本轮次 Q 函数求模型参数A，B，π

由于要极大化的参数在 E 步的式子中单独出现在3个项中，所有只需对各项分别逐一极大化

（1）第一项：

注意到满足约束条件（初始概率分布累加和为1），利用拉格朗日乘子法，写出拉格朗日函数：

对其求偏导数并令其结果为0：，得：

左右两边同时对 i 求和得到：，带入朗格朗日求导为零公式得：。可以看到，初始概率的最大似然估计就是传统统计法

（2）第二项：

同初始概率分布一样，转移概率同样也满足累加和为1的约束条件：，通过拉格朗日乘子法可以求出：

（3）第三项：

同样用拉格朗日乘子法，约束条件是：，求得：

Relevant Link:

 

6. 隐马尔科夫隐状态估计算法 - 隐状态概率矩阵最大似然估计

我们在本章节讨论隐马尔可夫模型隐状态序列估计的两种算法：近似算法、维特比算法（viterbi algorithm）

0x1: 近似算法

近似算法的思想是，在每个时刻 t 选择在该时刻最可能出现的状态，从而得到一个状态序列，将它作为预测的结果。给定隐马尔可夫模型和观测序列 O，在时刻 t 处于状态的概率是：，在每一时刻 t 最有可能的状态是：，从而得到状态序列

近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体是最优可能的状态序列（即不能保证全局最优），因为预测的状态序列可能有实际不发生的部分。同时，根据近似算法得到的状态序列中有可能存在转移概率为0的相邻状态（对某些i，j，aij = 0时）

0x2: 维特比算法

维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划（dynamic programming）求概率最大路径（最优路径）。这时一条路径对应着一个状态序列。

根据动态规划原理，最优路径具有这样的特征：如果最优路径在时刻 t 通过，那么这一路径从结点到终点的部分路径，对于从到终点的所有可能的部分路径集合来说，必须是最优的（即每步都要求局部最优）

依据这一原理，我们只需从时刻 t = 1开始，递推地计算在时刻 t，状态为 i 的各条部分路径的最大概率，在每一个 t = T计算最大概率对应的路径。最终得到最优路径序列，这就是维特比算法。

为了明确定义维特比算法，我们首先导入两个变量，（最大概率）和（最大概率对应的状态）。

定义在时刻 t 状态为 i 的所有单个单个路径中概率最大值为：，由此可得变量的递推公示：

定义在时刻 t 状态为 i 的所有单个路径中概率最大的路径的第 t - 1个结点为：

维特比算法的流程如下：

1. 初始化

2. 递推：对t = 2，3，...，T

3. 终止

 

4. 最优路径回溯：对t = T - 1，T - 2，....，1

得到最优路径：

0x3: 通过一个例子来说明维特比算法

还是盒子球的场景，模型，

，

已知观测序列，试求最优状态序列，即最优路径

我们应用维特比算法来解决这个问题

（1）初始化

在 t = 1时，对每一个状态 i，i = 1，2，3，求状态为 i 观测为红的概率，记此概率为，则

代入实际数据得：

（2）递推 t = 2

在时刻 t = 2，对每个状态i，i = 1，2，3，求在 t = 1时状态为 j 观测为红并在 t = 2时状态为 i 观测为白的路径的最大概率，记此最大概率为，则

同时，对每个状态i，i = 1，2，3，记录概率最大路径的前一个状态 j：

计算：

考虑上一轮所有可能状态，本轮的出现状态1的最大概率： = max｛0.1 * 0.5，0.16 * 0.3，0.28 * 0.2｝* 0.5 = 0.028。

考虑上一轮所有可能状态，本轮的出现状态2的最大概率： = max｛0.1 * 0.2，0.16 * 0.5，0.28 * 0.3｝* 0.6 = 0.0504。

考虑上一轮所有可能状态，本轮的出现状态3的最大概率： = max｛0.1 * 0.3，0.16 * 0.2，0.28 * 0.5｝* 0.7 = 0.098。

（3）递推 t = 3

 同样，在t = 3步，还是逐步引入t = 2步的所有概率最大概率，并结合t = 3步的转移概率和观测概率

 

计算：

（4）终止

以表示最优路径的概率，则，该结果是逐步递推出来的

最优路径的终点是：

（5）由最优路径的终点，逆向逆推最优路径序列

本轮最大概率的计算公式中，包含了上一轮次最大概率状态的结果

于是得到最优路径序列，即最优状态序列

笔者思考：

无论是计算观测序列概率的前向-后向算法，还是计算隐状态序列的维特比算法，本质上都是基于频数统计的极大似然估计，所依据的理论都是贝叶斯边缘概率累加公式。

同时我们也看到，每一步的计算需要考虑上一步的所有可能，这包含了一个思想，虽然上一步得到了局部最优但不一定就是全局最优，所以我们还不能完全“信任”上一步的argmax结果
当前本轮递推要把上一轮的所有可能都参与到本轮的计算中，在本轮重新计算一次似然概率。所以 t+1 步才确定 t 步的最大似然状态，每一轮的最大似然状态都要到下一轮才能得到确定。
在更高阶的N阶马尔科夫模型中，这个回溯要追溯到更早的 N 步前。

Relevant Link:

 

7. 隐马尔科夫模型的应用

在运用马尔科夫模型解决实际的问题的时候，我认为最重要的是正确理解我们要解决问题的本质，进行有效的抽象，将问题的各个维度套用到马尔科夫模型的三要素上。这相当于数学建模过程，完成建模之后就可以利用马尔科夫的学习和预测过程来帮助我们解决问题

0x1：序列标注问题

假设有4个盒子，每个盒子里都装有红白两种颜色的球，盒子里的红白球数由下表给出（等价于已知观测概率矩阵）

游戏的主办方按照如下的方法抽球，抽球的过程不让观察者看到，产生一个由球的颜色组成的观测序列：

1. 开始，从4个盒子里随机选取1个盒子（1/4等概率），从这个盒子里随机抽出1个球，记录其颜色后，放回；
2. 然后，从当前盒子随机转移到下一个盒子，规则是
　　1）如果当前盒子是盒子1，那么下一个盒子一定是2
　　2）如果当前盒子是2或3，那么分别以概率0.4和0.6转移到左边或右边的盒子
　　3）如果当前盒子是盒子4，那么各以0.5的概率停留在盒子4或者转移到盒子3
3. 确定转移的盒子后，再从这个盒子里随机抽出1个球，记录其颜色，放回；
4. 如此重复下去，重复进行5次

得到一个球的颜色的观测序列： O = ｛红，红，白，白，红｝
在这个过程中，观察者只能观测到球的颜色的序列，观测不到球是从哪个盒子取出的，即观测不到每次实验抽到盒子的隐状态序列。

这是一个典型的马尔科夫模型场景，根据所给条件，可以明确状态集合、观测集合、序列长度以及模型的三要素

盒子对应隐状态，隐状态的集合是：

球的颜色对应观测，观测的集合是：

状态序列和观测序列长度 T = 3

初始概率分布为：

状态转移概率分布为：

观测概率分布为：

观测集合V为：O = ｛红，红，白｝

要求解的问题是：在这次实验中，每次实验的盒子序列是什么。

0x2：根据观测数据推测最大似然的隐状态序列（序列解码问题）

值得注意的是，在进行实际问题解决的时候，很重要的一点是抽象能力，就是要想清楚哪个数据对应的是观测数据，哪个数据又是对应的隐状态序列。

例如下面的根据观测对象的日常行为，推测当前的天气的具体问题。

我们对一个观测对象进行6天的持续观测，该对象每天的行为有3种：walk：散步；shop：购物；clean：打扫卫生。

同时每天的天气有2种状态：Rainy：下雨；Sunny：晴天。

我们已知每天天气的转换概率，以及在不同天气下观测对象做不同行为的概率分布。

最后我们的目标是根据一系列的对观测对象在这6天的行为观测结果：[0, 2, 1, 1, 0, 2]，即[walk，clean，shop，shop，walk，clean]，反推出这6天最可能的每天的天气。

我们来编码实现一下

# -*- coding:utf-8 -*-

from __future__ import division
import numpy as np
from hmmlearn import hmm


states = ["Rainy", "Sunny"]   ## 隐藏状态类型
n_states = len(states)        ## 隐藏状态数量

observations = ["walk", "shop", "clean"]  ## 可观察的状态类型
n_observations = len(observations)        ## 可观察序列的状态数量

start_probability = np.array([0.6, 0.4])  ## 初始状态概率

## 状态转移概率矩阵
transition_probability = np.array([
  [0.7, 0.3],   # 晴天倾向保持晴天
  [0.4, 0.6]    # 阴天倾向转为晴天
])

## 观测序列概率矩阵
emission_probability = np.array([
  [0.1, 0.4, 0.5],
  [0.6, 0.3, 0.1]
])

# 构建了一个MultinomialHMM模型，这模型包括开始的转移概率，隐状态间的转移矩阵A（transmat），隐状态到观测序列的发射矩阵emissionprob，下面是参数初始化
model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability

# predict a sequence of hidden states based on visible states
bob_says = np.array([[0, 2, 1, 1, 0, 2]]).T  ##预测时的可见序列
print bob_says.shape
print bob_says
logprob, alice_hears = model.decode(bob_says, algorithm="viterbi")
print logprob ##该参数反映模型拟合的好坏

## 最后输出decode解码结果
print "Bob says(观测行为序列):", ", ".join(map(lambda x: observations[x[0]], bob_says))
print "Alice hears(天气序列)(隐状态序列):", ", ".join(map(lambda x: states[x], alice_hears))

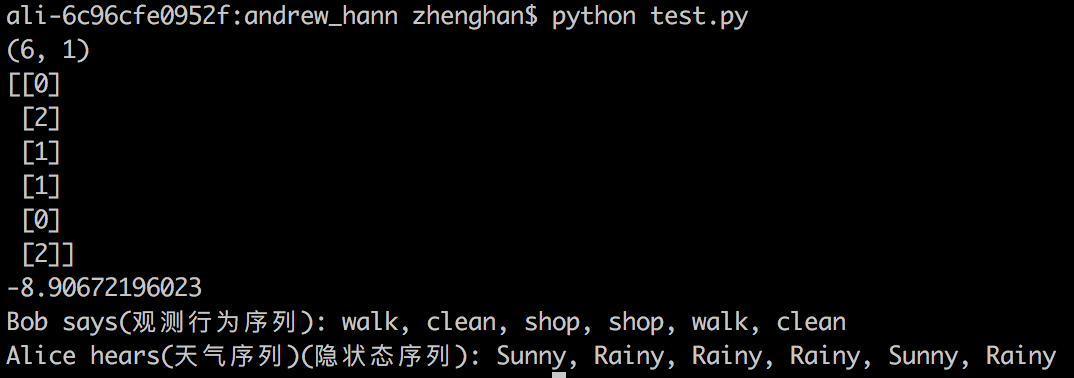
补充一句，如果是在语音识别问题中，观测数据就是音频流，需要估计的隐状态序列就是对应的发音文字

Relevant Link:

http://www.cs.ubc.ca/~murphyk/Bayes/rabiner.pdf
http://www.cnblogs.com/pinard/p/7001397.html
http://blog.csdn.net/u014365862/article/details/50412978
http://blog.csdn.net/yywan1314520/article/details/50533850
http://hmmlearn.readthedocs.io/en/latest/api.html
http://blog.csdn.net/wowotuo/article/details/40783357

0x3：学习问题和概率计算问题搭配使用 - 先根据观测数据（训练样本）train出一个模型（包含模型参数），然后基于这个模型预测新的样本（观测变量）的出现概率（即异常判断）

import numpy as np
from hmmlearn.hmm import GaussianHMM


###############################################################################
# Working with multiple sequences
X1 = [[0.5], [1.0], [-1.0], [0.42], [0.24]]
X2 = [[2.4], [4.2], [0.5], [-0.24]]

# concatenate them into a single array and then compute an array of sequence lengths:
X = np.concatenate([X1, X2])
lengths = [len(X1), len(X2)]

###############################################################################
# Run Gaussian HMM
print "fitting to HMM ..."

# Make an HMM instance and execute fit
# There is 4 type of states
model = GaussianHMM(n_components=4, n_iter=100).fit(X)

# Train the model parameters and hidden state
model_pre = model.fit(X, lengths)

###############################################################################
print "Compute the observation sequence log probability under the model parameters"
print model_pre.score(X1)

print "Compute the log probability under the model and compute posteriors."
print model_pre.score_samples(X1)

我们输入训练样本得到一组模型参数，之后基于这个模型参数预测接下来输入的观测序列出现的可能性，这常被用在文本异常检测的场景中。score方法返回的是LOG的结果，所以是负的，越接近0，表示越符合当前的HMM模型。

模型预测的观测序列的对数似然概率为：

-2.64250783257

0x4：学习问题和解码问题搭配使用 - 先根据观测数据（训练样本）train出一个模型（包含模型参数），然后基于这个模型预测在给定观测序列的情况下，最大似然的隐变量序列（及语音解码识别、解码问题）

import numpy as np
from hmmlearn.hmm import GaussianHMM


###############################################################################
# Working with multiple sequences
X1 = [[0.5], [1.0], [-1.0], [0.42], [0.24]]
X2 = [[2.4], [4.2], [0.5], [-0.24]]

# concatenate them into a single array and then compute an array of sequence lengths:
X = np.concatenate([X1, X2])
lengths = [len(X1), len(X2)]

###############################################################################
# Run Gaussian HMM
print "fitting to HMM ..."

# Make an HMM instance and execute fit
# There is 4 type of states
model = GaussianHMM(n_components=4, n_iter=100).fit(X)

# Train the model parameters and hidden state
model_pre = model.fit(X, lengths)


###############################################################################
print "Find most likely state sequence corresponding to X."
print model_pre.decode(X1)

print "pridect the mostly likly hidden state sequence according to the sample"
print model_pre.predict(X1)

print "Compute the posterior probability for each state in the model."
print model_pre.predict_proba(X1)

 

模型预测的隐变量序列概率分布为：

[[  4.28596850e-013   0.00000000e+000   1.00000000e+000   4.82112557e-178]
 [  1.00000000e+000   1.82778069e-311   3.61988083e-021   0.00000000e+000]
 [  1.00000000e+000   0.00000000e+000   7.31100741e-098   0.00000000e+000]
 [  7.17255159e-002   0.00000000e+000   9.28274484e-001   0.00000000e+000]
 [  9.97881894e-001   0.00000000e+000   2.11810616e-003   0.00000000e+000]]

模型预测的隐变量序列的结果为，其实我们根据概率分布取argmax也可以得到和api返回相同的结果

[2 0 0 2 0]

Relevant Link:

http://hmmlearn.readthedocs.io/en/stable/api.html
http://hmmlearn.readthedocs.io/en/stable/tutorial.html 

0x5：基于HMM进行文本异常检测

1. 以白找黑

如果我们能定义出一个场景，即正常的情况下文本的概率空间是集中在一个相对固定的范围内的（在一定的字符空间中进行状态转移），而异常的样本的字符空间及其字符间的转换关系极其不符合

正常的“模式”，这种情况就可以使用HMM。

# -*- coding: utf-8 -*-

import urllib
import urlparse
import re
from hmmlearn import hmm
import numpy as np
from sklearn.externals import joblib


MIN_LEN = 6     # 处理参数值的最小长度
N_Hidden = 10    # 隐状态个数（从领域经验来看，隐状态数量和观测变量的状态数量基本上应该持平）
T = -30  # 最大似然概率阈值
# URL中会出现的特殊字符
SEN = [
    '<',
    '>',
    ',',
    ':',
    '\'',
    '/',
    ';',
    '"',
    '{',
    '}',
    '(',
    ')'
]


# 排除中文干扰 只处理127以内的字符
def isascii(istr):
    if re.match(r'^(http)', istr):
        return False
    for i, c in enumerate(istr):
        if ord(c) > 127 or ord(c) < 31:
            return False
        if c in SEN:
            return True
    return True


# 特征离散规范化，减少参数状态空间
def etl(istr):
    vers = []
    for i, c in enumerate(istr):
        c = c.lower()
        if ord(c) >= ord('a') and ord(c) <= ord('z'):   # ascii字母
            vers.append([ord(c)])
        elif ord(c) >= ord('0') and  ord(c) <= ord('9'):    # 数字
            vers.append([1])
        elif c in SEN:
            vers.append([ord(c)])
        else:
            vers.append([2])
    return np.array(vers)


def extractvec(filename):
    X = [[0]]
    LINES = [['']]
    X_lens = [1]
    with open(filename) as f:
        for line in f:
            query = urllib.unquote(line.strip('\n'))  # url解码
            if len(line) >= MIN_LEN:
                params = urlparse.parse_qsl(query, True)
                for k, v in params:
                    if isascii(v) and len(v) >= N_Hidden:
                        vers = etl(v)  # 数据处理与特征提取
                        X = np.concatenate([X, vers])  # 每一个参数value作为一个特征向量
                        # # 通过np.concatenate整合成了一个1D长向量，同时需要额外传入len list来标明每个序列的长度边界
                        X_lens.append(len(vers))  # 长度
                        LINES.append(v)
    return X, X_lens, LINES


def train(filename):
    X, X_lens, LINES = extractvec(filename)
    remodel = hmm.GaussianHMM(n_components=N_Hidden, covariance_type="full", n_iter=100)
    remodel.fit(X, X_lens)
    joblib.dump(remodel, "../model/xss-train.pkl")
    return remodel


def predict(filename):
    remodel = joblib.load("../model/xss-train.pkl")
    X, X_lens, LINES = extractvec(filename)
    LINES = LINES[1:]
    X = X[1:, :]
    X_lens = X_lens[1:]
    lastindex = 0
    for i in range(len(X_lens)):
        line = np.array(X[lastindex:lastindex+X_lens[i], :])
        lastindex += X_lens[i] 
        pros = remodel.score(line)
        if pros < T:
            print "Find bad sample POR: %d LINE:%s" % (pros, LINES[i])


if __name__ == '__main__':
    # 以白找黑，给HMM输入纯白样本，让其记住正常url参数的模型转化概率
    # remodel = train("../data/web-attack/normal-10000.txt")    # train a GMM model with train sample

    # 输入待检测样本，设定一个阈值(score的分值越小，说明出现的概率越小，也即说明偏离正常样本的程度)
    predict("../data/xss-20.txt")
    # predict the probability of the new sample according to the model(abnormal detection)

我们将黑白待检测样本混合在一起，看HMM的预测效果如何

2. 以黑找黑

# -*- coding:utf-8 -*-

import sys
import urllib
import urlparse
import re
from hmmlearn import hmm
import numpy as np
from sklearn.externals import joblib
import HTMLParser
import nltk

MIN_LEN = 10    # 处理参数值的最小长度
N = 5   # 状态个数
T = -200    # 最大似然概率阈值
SEN = ['<', '>', ',', ':', '\'', '/', ';', '"', '{', '}', '(', ')']  #其他字符2
index_wordbag = 1     # 词袋索引
wordbag = {}    # 词袋


# 数据提取与特征提取，这一步我们不采用单字符的char特征提取，而是根据领域经验对特定的phrase字符组为基础单位，进行特征化，这是一种token切分方案

# </script><script>alert(String.fromCharCode(88,83,83))</script>
# <IMG SRC=x onchange="alert(String.fromCharCode(88,83,83))">
# <;IFRAME SRC=http://ha.ckers.org/scriptlet.html <;
# ';alert(String.fromCharCode(88,83,83))//\';alert(String.fromCharCode(88,83,83))//";alert(String.fromCharCode(88,83,83))
# //\";alert(String.fromCharCode(88,83,83))//--></SCRIPT>">'><SCRIPT>alert(String.fromCharCode(88,83,83))</SCRIPT>
tokens_pattern = r'''(?x)
 "[^"]+"
|http://\S+
|</\w+>
|<\w+>
|<\w+
|\w+=
|>
|\w+\([^<]+\) #函数 比如alert(String.fromCharCode(88,83,83))
|\w+
'''


def split_tokens(line, tokens_pattern):
    tokens = nltk.regexp_tokenize(line, tokens_pattern)
    return tokens

def load_wordbag(filename, max=100):
    X = [[0]]
    X_lens = [1]
    tokens_list = []
    global wordbag
    global index_wordbag

    with open(filename) as f:
        for line in f:
            line = line.strip('\n')
            line = urllib.unquote(line)   # url解码
            #h = HTMLParser.HTMLParser()    # 处理html转义字符
            #line = h.unescape(line)
            if len(line) >= MIN_LEN:  # 忽略短url value
                line, number = re.subn(r'\d+', "8", line)   # 数字常量替换成8
                line, number = re.subn(r'(http|https)://[a-zA-Z0-9\.@&/#!#\?:=]+', "http://u", line)    # ulr日换成http://u
                line, number = re.subn(r'\/\*.?\*\/', "", line)     # 去除注释
                tokens = split_tokens(line, tokens_pattern)  # token切分
                tokens_list += tokens

    fredist = nltk.FreqDist(tokens_list)  # 单文件词频
    keys = fredist.keys()
    keys = keys[:max]     # 降维，只提取前N个高频使用的单词，其余规范化到0
    for localkey in keys:  # 获取统计后的不重复词集
        if localkey in wordbag.keys():  # 判断该词是否已在词袋中
            continue
        else:
            wordbag[localkey] = index_wordbag
            index_wordbag += 1
    print "GET wordbag", wordbag
    print "GET wordbag size(%d)" % index_wordbag


def train(filename):
    X = [[-1]]
    X_lens = [1]
    global wordbag
    global index_wordbag

    with open(filename) as f:
        for line in f:
            line = line.strip('\n')
            line = urllib.unquote(line)   # url解码
            #h = HTMLParser.HTMLParser() # 处理html转义字符
            #line = h.unescape(line)
            if len(line) >= MIN_LEN:
                line, number = re.subn(r'\d+', "8", line)   # 数字常量替换成8
                line, number = re.subn(r'(http|https)://[a-zA-Z0-9\.@&/#!#\?:]+', "http://u", line)     # ulr日换成http://u
                line, number = re.subn(r'\/\*.?\*\/', "", line)     # 干掉注释
                words = split_tokens(line, tokens_pattern)
                vers = []
                for word in words:
                    # 根据词汇编码表进行index编码，对不在词汇表中的token词不予编码
                    if word in wordbag.keys():
                        vers.append([wordbag[word]])
                    else:
                        vers.append([-1])

            np_vers = np.array(vers)
            X = np.concatenate([X, np_vers])
            X_lens.append(len(np_vers))

    remodel = hmm.GaussianHMM(n_components=N, covariance_type="full", n_iter=100)
    remodel.fit(X, X_lens)
    joblib.dump(remodel, "../model/find_black_with_black-xss-train.pkl")

    return remodel


def test(remodel, filename):
    with open(filename) as f:
        for line in f:
            line = line.strip('\n')
            line = urllib.unquote(line)     # url解码
            # 处理html转义字符
            #h = HTMLParser.HTMLParser()
            #line = h.unescape(line)

            if len(line) >= MIN_LEN:
                line, number = re.subn(r'\d+', "8", line)      # 数字常量替换成8
                line, number = re.subn(r'(http|https)://[a-zA-Z0-9\.@&/#!#\?:]+', "http://u", line)     # ulr日换成http://u
                line, number = re.subn(r'\/\*.?\*\/', "", line)     # 干掉注释
                words = split_tokens(line)
                vers = []
                for word in words:
                    # test和train保持相同的编码方式
                    if word in wordbag.keys():
                        vers.append([wordbag[word]])
                    else:
                        vers.append([-1])

                np_vers = np.array(vers)
                pro = remodel.score(np_vers)
                if pro >= T:
                    print "SCORE:(%d) XSS_URL:(%s) " % (pro, line)


if __name__ == '__main__':
    train_filename = "../data/xss-200000.txt"
    # 基于训练样本集（纯黑，我们这里是以黑找黑），得到词频编码表
    load_wordbag(train_filename, 2000)

    # 基于同样的训练样本集（纯黑，我们这里是以黑找黑），训练HMM模型
    remodel = train(train_filename)

    # 基于训练得到的HMM模型，对未知样本的最大似然概率进行预测（即预测未知样本观测序列出现的可能性，即找类似的黑样本）
    test(remodel, "../data/xss-20.txt")

整个过程分为：

泛化 -> 分词 -> 词集编码 -> 词集模型处理流程

0x6：将HMM的对数似然概率预测值作为特征

我们可以采用类似于DNN中隐层的思想，将HMM的对数似然概率输出作为一个抽象后的特征值，甚至可以作为新的一份样本特征输入到下一层的算法模型中参与训练。

# -*- coding:utf-8 -*-

import sys
import urllib
import urlparse
import re
from hmmlearn import hmm
import numpy as np
from sklearn.externals import joblib
import HTMLParser
import nltk
import csv
import matplotlib.pyplot as plt

MIN_LEN = 10    # 处理域名的最小长度
N = 8     # 状态个数
T = -50   # 最大似然概率阈值
FILE_MODEL = "../model/12-4.m"     # 模型文件名


def load_alexa(filename):
    domain_list = []
    csv_reader = csv.reader(open(filename))
    for row in csv_reader:
        domain = row[1]
        if domain >= MIN_LEN:
            domain_list.append(domain)
    return domain_list


def domain2ver(domain):
    ver = []
    for i in range(0, len(domain)):
        ver.append([ord(domain[i])])
    return ver

def train_hmm(domain_list):
    X = [[0]]
    X_lens = [1]
    for domain in domain_list:
        ver = domain2ver(domain)    # 逐字符ascii向量化
        np_ver = np.array(ver)
        X = np.concatenate([X, np_ver])
        X_lens.append(len(np_ver))

    remodel = hmm.GaussianHMM(n_components=N, covariance_type="full", n_iter=100)
    remodel.fit(X, X_lens)
    joblib.dump(remodel, FILE_MODEL)

    return remodel


def load_dga(filename):
    domain_list = []
    # xsxqeadsbgvpdke.co.uk,Domain used by Cryptolocker - Flashback DGA for 13 Apr 2017,2017-04-13,
    # http://osint.bambenekconsulting.com/manual/cl.txt
    with open(filename) as f:
        for line in f:
            domain = line.split(",")[0]
            if domain >= MIN_LEN:
                domain_list.append(domain)
    return domain_list


def test_dga(remodel,filename):
    x = []
    y = []
    dga_cryptolocke_list = load_dga(filename)
    for domain in dga_cryptolocke_list:
        domain_ver = domain2ver(domain)
        np_ver = np.array(domain_ver)
        pro = remodel.score(np_ver)
        x.append(len(domain))
        y.append(pro)
    return x, y


def test_alexa(remodel,filename):
    x=[]
    y=[]
    alexa_list = load_alexa(filename)
    for domain in alexa_list:
        domain_ver = domain2ver(domain)
        np_ver = np.array(domain_ver)
        pro = remodel.score(np_ver)
        x.append(len(domain))
        y.append(pro)
    return x, y


if __name__ == '__main__':
    domain_list = load_alexa("../data/top-1000.csv")
    # remodel = train_hmm(domain_list)    # 以白找黑: 基于alexa域名数据训练hmm模型
    remodel = joblib.load(FILE_MODEL)
    x_3, y_3 = test_dga(remodel, "../data/dga-post-tovar-goz-1000.txt")
    x_2, y_2 = test_dga(remodel,"../data/dga-cryptolocke-1000.txt")
    fig, ax = plt.subplots()
    ax.set_xlabel('Domain Length')      # 横轴是域名长度
    ax.set_ylabel('HMM Score')          # 纵轴是hmm对观测序列计算得到的似然概率
    ax.scatter(x_3, y_3, color='b', label="dga_post-tovar-goz")
    ax.scatter(x_2, y_2, color='g', label="dga_cryptolock") 
    ax.legend(loc='right')
    plt.show()

我们以域名长度为横轴，以HMM值作为纵轴，从可视化结果可以看到，HMM作为DGA域名区分的一个变量，有一定的区分型，展现出了一定的规律。

0x7：利用HMM实现分词任务

例如在分词任务中，中文的句子“请问今天的天气怎么样？”就是可以被观测到的序列，而其分词的标记序列就是未知的状态序列“请问/今天/深圳/的/天气/怎么样/？”这种分词方式对应的标记序列为“BEBEBESBEBME”。

标记序列：标签方案中通常都使用一些简短的英文字符[串]来编码。

标签列表如下，在分词任务中，通常用BMES标记。

• B，即Begin，表示开始
• M，即Mediate，表示中间
• E，即End，表示结尾
• S，即Single，表示单个字符

参考链接：

https://mp.weixin.qq.com/s?__biz=MzA3NDIyMjM1NA==&mid=2649033804&idx=2&sn=faf79533669416849e807a0aeb2c7eee&chksm=8712b231b0653b27f94018743d6f4f64582a2a29d3caa01d61e71cfaf89a8d32dbcb877e105e&scene=21#wechat_redirect