Educational Codeforces Round 26 [ D. Round Subset ] [ E. Vasya's Function ] [ F. Prefix Sums ]
PROBLEM D - Round Subset
题
OvO http://codeforces.com/contest/837/problem/D
837D
解
DP,
dp[i][j]代表已经选择了i个元素,当2的个数为j的时候5的个数的最大值
得注意最大值(貌似因为这个喵呜了一大片喵~☆)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
const int M=64*202;
const int N=M-2;
int n,k;
int f[222][M]; //f[i][j] used num=i, sum of k2=j, val of f[i][j] = max sum of k5
int k2[222],k5[222];
void init()
{
memset(k2,0,sizeof(k2));
memset(k5,0,sizeof(k5));
memset(f,-1,sizeof(f));
}
int main()
{
int i,j,t;
ll tmp;
cin>>n>>k;
init();
for(i=1;i<=n;i++)
{
scanf("%I64d",&tmp);
while(tmp%2==0)
tmp/=2,k2[i]++;
while(tmp%5==0)
tmp/=5,k5[i]++;
}
f[0][0]=0;
for(i=1;i<=n;i++)
for(j=k;j>=1;j--)
for(t=N;t>=k2[i];t--)
if(f[j-1][t-k2[i]]!=-1)
f[j][t]=max(f[j][t],f[j-1][t-k2[i]]+k5[i]);
int ans=0;
for(t=0;t<=N;t++)
ans=max(ans,min(t,f[k][t]));
cout<<ans<<endl;
return 0;
}
PROBLEM E - Round Subset
题
OvO http://codeforces.com/contest/837/problem/E
837E
解
当B和A公约数不为1的时候(开始的时候,或者B减了一定次数1的时候),就相当于A和B同除以gcd(A,B),然后B继续一次减1。
这样只要每次计算出每次B要减多少次1才能和A有不为1的公约数。
那么预处理出A的质因数,然后每次对A的质因数判断一下,哪个最近(也就是模最小)即可。
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll M=1e6+44;
const ll inf=1e18;
ll A,B;
ll prim[M];
ll lp,nump[M];
ll ans;
void init(ll spl)
{
ll i,j;
lp=0;
for(i=2;i*i<=spl;i++)
if(spl%i==0)
{
prim[++lp]=i;
nump[lp]=0;
while(spl%i==0)
spl/=i,nump[lp]++;
}
if(spl!=1)
{
prim[++lp]=spl;
nump[lp]=1;
}
}
void deal()
{
if(B==0)
return ;
if(A==1)
{
ans+=B;
return ;
}
ll i,j,mn;
ll tmp,gcd;
mn=inf;
for(i=1;i<=lp;i++)
{
tmp=B%prim[i];
if(tmp<mn)
mn=tmp;
}
tmp=mn;
ans+=tmp;
B-=tmp;
gcd=__gcd(A,B);
A/=gcd; B/=gcd;
for(i=1;i<=lp;i++)
if(gcd%prim[i]==0)
{
while(gcd%prim[i]==0)
gcd/=prim[i],nump[i]--;
if(nump[i]==0)
{
swap(nump[i],nump[lp]);
swap(prim[i],prim[lp]);
lp--; i--;
}
}
deal();
}
void solve()
{
ans=0;
deal();
printf("%I64d\n",ans);
}
int main()
{
scanf("%I64d%I64d",&A,&B);
init(A);
solve();
return 0;
}
PROBLEM F - Prefix Sums
题
OvO http://codeforces.com/contest/837/problem/F
837F
解
由于新生成的m+1个数列第一个肯定为0,所以可以忽略掉,当作每次新生成的数列只拥有m个元素
然后 举个栗子
当s={1,0,0,0,0} 可以得到如下矩阵
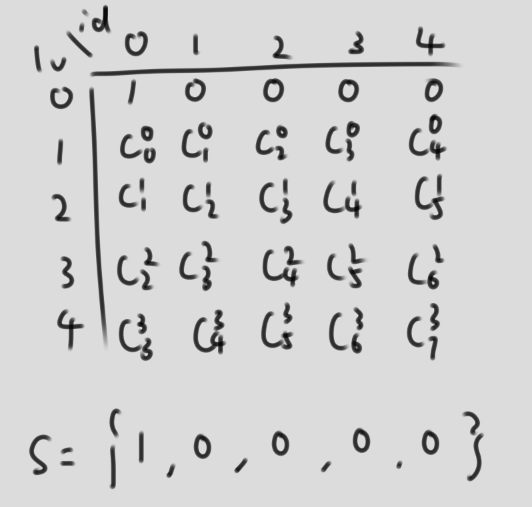
显然这拥有某神秘三角的性质
然后二分答案,每次通过组合数来算就行了,由于太大直接退出,所以不会超时(如果C(p,q),p-q<q的话,转化为C(p,p-q))
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll M=2e5+44;
ll n,k;
ll sum;
ll s[M];
bool check(ll spl)
{
ll i,j,t,x,y,p,q;
double sum=0,tmp;
for(t=0;t<n;t++)
{
if(s[t]==0) continue;
x=spl; y=(n-1)-t; //s[i]*c(y+x-1,x-1)
p=x-1; q=x+y-1; //c(q,p)
p=min(q-p,p);
tmp=s[t];
for(i=q,j=p;j>=1;j--,i--)
{
tmp=tmp*i/j;
if(tmp>=k)
return true;
}
sum+=tmp;
if(sum>=k) return true;
}
return false;
}
void solve()
{
ll li=0,ri=k,mid;
while(li<ri-1)
{
// cout<<li<<' '<<ri<<endl;
mid=(li+ri)>>1;
if(check(mid))
ri=mid;
else
li=mid;
}
cout<<ri<<endl;
}
int main()
{
ll i,j,tmp;
cin>>n>>k;
for(i=0;i<n;i++)
{
scanf("%I64d",&s[i]);
if(s[i]>=k)
{
printf("0\n");
return 0;
}
}
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号