随机场(Random Field)是在同一向量空间上一组随机变量组成的集合。通常情况下我们将存在相关关系的一组随机变量作为随机场进行研究。通常我们使用λ来表示一个参数给定的随机场。
概率图模型采用图来表示随机变量之间的相关关系, 最常见的概率图模型是采用有向无环图的贝叶斯网络和采用无向图的马尔科夫随机场。
马尔科夫随机场遵循马尔科夫假设, 即在随机过程中下一个状态仅与当前状态有关, 与历史状态无关。
最简单的马尔科夫随机场的概率图是链式的, 除了两端外其它节点上的随机变量只与相邻的两个节点有关, 我们将这种模型称为马尔科夫链。
马尔科夫随机场常用于分析随机过程, 随机场上每一个节点代表随机系统在某个时刻可能处于的一个状态, 节点对应的随机变量代表了某个时刻系统处于该状态的概率。
给定系统初始时刻处于各个状态的概率,每个节点依据与它相邻的节点的先验概率计算下一时刻系统处于该状态的概率。 逐次迭代,观测变量的概率分布将会生成一个可以描述随机过程的时间序列, 我们称为观测序列。
隐马尔科夫模型(Hiden Markov Model, HMM)增加了一组观测随机变量, 一条隐藏的马尔科夫链将产生一个不可观测的随机过程。链上每个节点先验结果将在观测变量上产生一个可观测的概率分布,我们可以借助观测变量分析隐马尔科夫链上的随机过程。
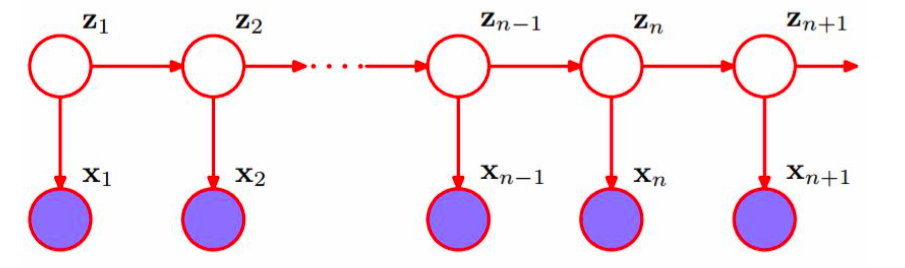
除了马尔科夫假设外, HMM显然依赖一个严格的观测独立性假设,即观测结果仅依赖马尔科夫链当前的状态与其它时刻的状态和观测无关。
我们可以使用三个要素来描述一个含有N个状态M个观测值的HMM模型:
-
初始状态概率向量π:N维向量, 表示初始时刻随机过程处于对应状态的概率。
-
状态转移概率矩阵A: N * N 矩阵, a[i,j]表示从状态i转移到j的概率.
-
观测转移概率矩阵B: N * M矩阵, b[j, k]表示处于状态j时产生观测值k的概率。
HMM有三类基本问题:
-
概率计算问题: 计算给定模型下出现特定观测序列的概率。
-
学习问题, 又称参数估计问题: 给定观测序列, 调整模型参数使得给定观测序列出现的概率P(O|λ)最大。
-
预测问题, 又称解码问题: 给定模型, 求使观测序列出现概率最大的状态序列。
示例: 这里以天气与地面湿度为例来说明HMM中三类问题求解的方法。
我们将天气分为3个等级, 不同天气下地面湿度不同, 观察者只能观察地面湿度无法直接观察天气。
假设地面湿度仅与当天天气有关,每种天气导致地面湿度的概率为:
| 天气 |
晴 |
多云 |
阴 |
雨 |
| 干燥 |
0.8 |
0.6 |
0.5 |
0.2 |
| 湿润 |
0.2 |
0.4 |
0.5 |
0.8 |
为了便于表示,下文使用wet, dry代表湿润和干燥两种状态。
假设每天天气仅与前一天天气有关, 之间的概率关系为:
-
若今天为晴,0.5的概率明天为晴, 0.5的概率明天多云
-
若今天为多云,0.4的概率明天为晴, 0.6的概率明天阴
-
若今天为阴,0.7的概率明天为雨, 0.3的概率明天为多云
-
若今天为雨,0.2的概率明天为多云, 0.3的概率明天为阴, 0.5的概率明天为雨
根据统计,一年中四种天气占得的比例为(0.3, 0.1, 0.2, 0.4)
该示例中的随机过程可以用HMM模型描述, 示例中存在两个假设:
-
地面湿度仅与当天天气有关: 观测独立性假设
-
每天的天气仅与前一天有关: 马尔科夫假设
从这个示例中可以看出, HMM模型的假设相当严格在使用时应慎重。
该示例中存在两个序列:
根据天气的统计数据得到初始状态矩阵:
\[\pi = (0.3, 0.1, 0.2, 0.4)
\]
根据盒子转移的规则,写出状态转移矩阵:
\[A = \left[
\begin{array}{ccc}
0.5 & 0.5 & 0 & 0 \\
0.4 & 0 & 0.6 & 0 \\
0 & 0.7 & 0 & 0.3 \\
0 & 0.2 & 0.3 & 0.5 \\
\end{array}
\right]
\]
使用行向量\(pi_i\)表示某一天各天气的概率, p * A即为下一天各天气的概率:
\[pi_1 = pi * A = (0.19, 0.37, 0.18, 0.26)
\]
根据每种天气下地面湿度的概率,写出观测转移矩阵:
\[B = \left[
\begin{array}{ccc}
0.8 & 0.2 \\
0.6 & 0.4 \\
0.5 & 0.5 \\
0.2 & 0.8 \\
\end{array}
\right]
\]
使用行向量\(pi_i\)表示某一天各天气的概率, p * B即为当天地面各湿度状态的概率:
\[o = \pi * B = (0.48, 0.52)
\]
常见资料中常以小写英文字母表示矩阵的元素,本问题中下标仅表示时间
用A[i,j]表示矩阵A中第i行j列的元素, 行号与列号均从1开始
概率计算问题
HMM的定义给出了计算给定模型下出现特定观测序列概率的方法,状态序列概率:
\[P(I\mid\lambda)=P(i_1)P(i_2\mid i_1)\cdots P(i_T\mid i_{T-1})= \pi[i_1] * A[i_1,i_2] \cdots A[i_{T-1},i_T]
\]
给定状态序列下, 观测序列概率:
\[P(O\mid I, \lambda)=P(o_1\mid i_1)\cdots P(o_T\mid i_T)=B[i_1,o_1]* B[i_2,o_2] \cdots B[i_T,(o_T]
\]
上式中,\(o_i\)表示观测序列中第i个元素。给定模型下观测序列条件概率:
\[P(O\mid\lambda)=\sum_I P(O\mid I, \lambda)P(I\mid\lambda)=\sum_{\underbrace{i_1,i_2, \cdots ,i_T}_{N\times N\times \cdots \times N}}\pi[i_1] * A[i_1,i_2] * B[i_1,o_1] \cdots A[i_{T-1},i_T]*B[i_T,o_T]
\]
但是该方法几乎穷举了所有可能的观测序列, 时间复杂度高达\(O(TN^T)\)。
前向-后向算法通过部分概率和减少了计算量。
给定模型λ, 定义到时刻t出现部分观测序列\(O_t\)且当前状态为\(p_i\)的概率为前向概率, 记作:
\[\alpha_t(i) = P(O_{1,2, \cdots t},p_i | \lambda)
\]
α在t=1时的初值为:
\[\alpha_1(i)=\pi_i * B[i,o_1],\quad i=1,2,\cdots,N
\]
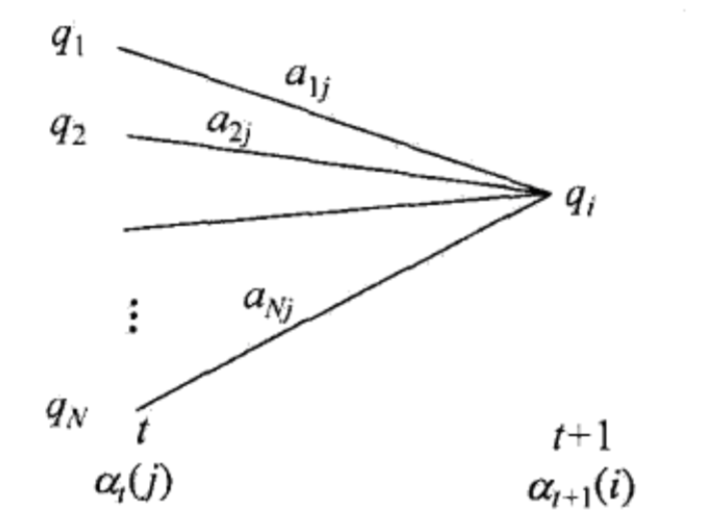
通过递推得到α的后续值:
\[\alpha_{t+1}(i)= \sum_{j=1}^N(\alpha_t(j) * a[j,i]) * b[i,o_{t+1}] \quad i=1,2,\cdots,N
\]
最终得到给定观测序列概率P(O|λ):
\[P(O\mid \lambda)=\sum_{i=1}^N\alpha_T(i)
\]
时间复杂度大为降低, 其原因在于α递推过程中避免了计算不需要的部分概率和。
类似地可以定义后向概率:
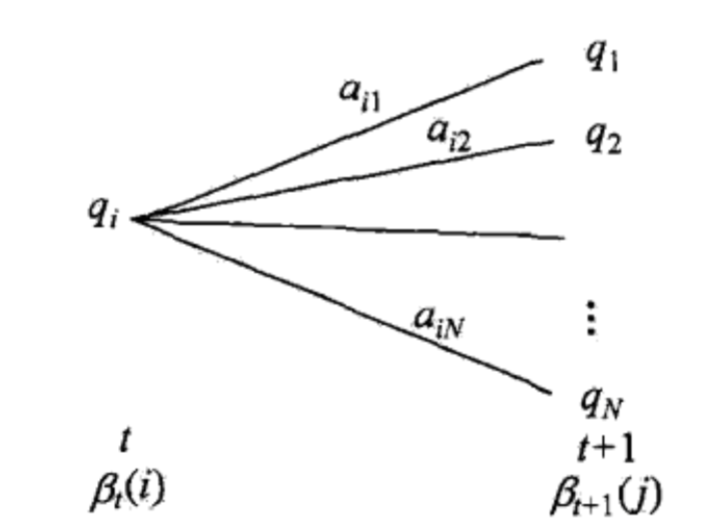
\[\beta_t(i) = P(O_{t+1, \cdots T}, p_i | \lambda)
\]
初值, 注意后向法是从后向前递推的:
\[\beta_T(i)=1,\quad i=1,2,\cdots,N
\]
得到给定观测序列概率P(O|λ):
\[P(O\mid \lambda)=\sum_{i=1}^N\pi_i b[i,o_1]\beta_1(i)
\]
给定HMM模型:
\[A = \left[
\begin{array}{ccc}
0.5 & 0.2 & 0.3 \\
0.3 & 0.5 & 0.2 \\
0.2 & 0.3 & 0.5 \\
\end{array}
\right]
\]
\[B = \left[
\begin{array}{ccc}
0.5 & 0.5 \\
0.4 & 0.6 \\
0.7 & 0.3 \\
\end{array}
\right]
\]
\[\pi = (0.2, 0.4, 0.4)
O = (1, 2, 1)
\]
(1)求初值:
\[\alpha_1(1) = \pi_0[1] * B[1,1] = 0.2 * 0.5 = 0.1 \\
\alpha_1(2) = \pi_0[2] * B[2,1] = 0.4 * 0.4 = 0.16 \\
\alpha_1(3) = \pi_0[3] * B[3,1] = 0.4 * 0.7 = 0.28
\]
(2)递推
\[\alpha_2(1) = \sum_{j=1}^3(\alpha_1(j) * A[j, 1] )* B[1,2] = (0.1 * 0.5 + 0.16 * 0.3 + 0.28 * 0.2 ) * 0.5 = 0.077 \\
\alpha_2(2) = \sum_{j=1}^3(\alpha_1(j) * A[j, 2] )* B[2,2] = (0.1 * 0.2 + 0.16 * 0.5 + 0.28 * 0.3 ) * 0.6 = 0.1104 \\
\alpha_2(3) = \sum_{j=1}^3(\alpha_1(j) * A[j, 3] )* B[3,2] = (0.1 * 0.3+ 0.16* 0.2 + 0.28 * 0 .5 ) * 0.3 = 0.0606
\]
\[\alpha_3(1) = \sum_{j=1}^4(\alpha_2(j) * A[j, 1] )* B[1,1] = 0.04187\\
\alpha_3(2) = \sum_{j=1}^4(\alpha_2(j) * A[j, 2] )* B[2,1] = 0.03551 \\
\alpha_3(3) = \sum_{j=1}^4(\alpha_2(j) * A[j, 3] )* B[3,1] = 0.05284 \\
\]
(3)求概率
\[P(O | \lambda) = \sum_{j=1}^3[\alpha_3(j)] = 0.13022
\]
参数估计问题
参数估计问题或称为学习问题, 是指如何调整模型参数使得给定观测序列出现的概率P(O|λ)最大的问题。根据训练中是否给出了与观测序列对应的状态序列分为监督学习方法和非监督学习方法。
监督学习需要训练数据中提供随机过程中的状态序列和观测序列,非监督学习只需提供观测序列。 在拥有状态序列时可以直接使用训练样本中状态转移的频率估计概率。
最大期望算法(Expectation-Maximization algorithm, EM)是一种极大似然参数估计法, 适用于依赖于隐藏变量的概率模型, 隐马尔科夫模型是其典型的应用场景。
EM算法进行多次迭代对参数值进行估计,每次迭代分为计算期望和最大化两步。
HMM的非监督学习方法即是著名的Baum-Welch算法, 它是EM算法在HMM中的特例。监督学习依赖人工标注的数据过多, 实际应用中我们通常选择Baum-Welch算法进行训练。
Baum-Welch算法只需要S个长度为T的观测序列就可进行训练。首先隐马尔科夫模型是一个含有隐变量的概率模型:
\[P(O|\lambda) = \sum P(O|I,\lambda)P(I|\lambda)
\]
确定模型全数据的对数似然函数\(log P(O,I|\lambda)\),根据EM算法写出Q函数:
\[Q(\lambda|\lambda \overline) = \sum log P(O,I|\lambda)P(O,I|\lambda \overline)
\]
其中\(\lambda*\)是参数的当前估计值, \(\lambda\)是要极大化的模型参数。即EM算法中的计算期望。
代入概率表达式:
\[P(O,I\mid\lambda)=P(O\mid I, \lambda)P(I\mid\lambda)=\pi_{i_1} * a[i_1,i_2] * b[i_1,o_1] \cdots a[i_{T-1},i_T] * b[i_T,o_T]
\]
将Q改写为:
\[Q(\lambda,\overline{\lambda})=\sum_Ilog\pi_{i_1}P(O,I|,\overline{\lambda})+\sum_I\left(\sum_{t=1}^{T-1}log\ a[i_t,i_{t+1}]\right)P(O,I|,\overline{\lambda})+\sum_I\left(\sum_{t=1}^{T}log\ b[i_t,o_t]\right)P(O,I|,\overline{\lambda})
\]
展开上式的第一项:
\[\sum_Ilog\pi_{i_1}P(O,I|,\overline{\lambda}) = \sum_{i=1}^Nlog\pi_{i}P(O,i_1=i|,\overline{\lambda})
\]
注意到\(\sum \pi_{i} = 1\), 对各项使用拉格朗日乘子法极大化, 求出最优参数:
\[\pi_i = \frac{P(O,i_1=i|,\overline{\lambda})}{P(O|\overline{\lambda})} = \gamma_1(i)
\]
\[a_{ij} = \frac{\sum_{t=1}^{T-1}P(O,i_t=i,i_{t+1}=j|,\overline{\lambda})}{\sum_{t=1}^{T-1}P(O,i_t=i|,\overline{\lambda})} = \frac{\sum_{t=1}^{T-1}\xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma_t(j)}
\]
\[b_{jk} = \frac{\sum_{t=1,o_t=v_k}^{T}P(O,i_t=j|,\overline{\lambda})}{\sum_{t=1}^{T}P(O,i_t=j|,\overline{\lambda})}= \frac{\sum_{t=1,o_t=v_k}^{T}\gamma_t(j)}{\sum_{t=1}^{T}\gamma_t(j)}
\]
注意到上述表达式中出现了一些特殊的概率值, 在t时刻处于i状态的概率:
\[\gamma_t(i)=P(i_t=q_i|O,\lambda)=\frac{P(i_t=q_i,O|\lambda)}{P(O|\lambda)}=\frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^N\alpha_t(j)\beta_t(j)}
\]
在时刻t处于i状态, 时刻t+1处于j状态的概率:
\[\xi_t(i,j)=P(i_t=q_i,i_{t+1}=q_j|O,\lambda)=\frac{P(i_t=q_i,i_{t+1}=q_j,O|\lambda)}{P(O|\lambda)}=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{i=1}^N\sum_{j=1}^N\alpha_t(i) * a[i,j] * b[j,o_{t+1}] * \beta_{t+1}(j)}
\]
将它们代入参数估计式中, 即可得到最终表达式。
解码问题
解码问题是指,给定模型参数 求使给定观测序列出现概率最大的状态序列的问题,即最大化P(I | O, λ)的问题。很容易想到的估计方法是选择使得各时刻系统处于i状态的概率最大的状态作为该时刻状态:
\[I = arg\quad max\quad \gamma_t(i)
\]
然而这种方法容易陷入局部最优解, 更有效的方法是采用Viterbi算法估计全局最优解。
每个状态序列都对应着一条状态转移路径,最可能的状态序列对应的路径出现概率也最高。如果我们把出现的概率定义为路径的代价话, 我们就可以使用最优路径算法求得出现概率最高的专业路径。
Viterbi算法即采用动态规划算法求得这条最优路径(概率最大路径)。引入变量\(\delta\)表示在时刻t状态为i的所有路径中最大概率值:
\[\delta_t(i)=\max_{i_1,i_2,...,i_{t-1}}P(i_t=i,i_{t-1},...,i_1,o_t,...,o_1|\lambda)
\]
定义最优路径中t-1个节点为:
\[\psi_t(i) = arg \quad max \quad \big[ \delta_{t-1}(j) a[j,i] \big]
\]
初始化:
\[\delta_1(i) = \pi_ib[i,o_1]
\]
\[\psi_1(i) = 0
\]
递推:
\[\delta_t(i) = max(\delta_{t-1}(j)a[j,i]) * b[i,o_t]
\]
\[\psi_t(i) = arg \quad max(\delta_{t-1}(j)*a[j,i])
\]
回溯:
\[i_t^* = \psi_{t+1}(i_{t+1}^*)
\]
求得的\(i_t\)序列即为所求状态序列
Keep working, we will find a way out.
This is Finley, welcome to join us.




