四边形不等式优化DP
记录一下,以免忘了
对于一个形如
\[dp[i][j]=min(dp[i][k]+dp[k][j]+w[i][j])
\]
的转移方程(注意取最大值时不一定满足四边形不等式)
定理1
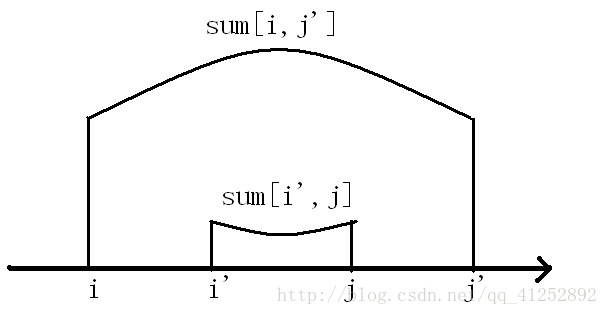
若对于\(a \leq b\leq c \leq d\)且\(w_{b,c}\leq w_{a,d}\)
那么我们称\(w\)关于区间包含关系单调
定理2
若对于\(a \leq b\leq c \leq d\)且\(w_{a,c}+w_{b,d}\leq w_{b,c}+w_{a,d}\)
则称\(w\)满足四边形不等式

性质1
若\(w\)满足四边形不等式,当且仅当\(w_{i,j}+w_{i+1,j+1}\leq w_{i+1,j}+w_{i,j+1}\)
(没啥卵用)
性质2
若\(w\)满足四边形不等式,且关于区间包含关系单调
则\(dp\)也满足四边形不等式
性质3
设\(s_{i,j}\)为\(dp_{i,j}\)的决策点,若\(dp\)满足四边形不等式
那么\(s_{i,j-1}\leq s_{i,j} \leq s_{i+1,j}\)
证明
放一个不错的博客
例题
石子归并加强版
其实这题并不是极限数据,再强一点的可以去百度SDOI2008石子归并,据说要用平衡树维护某G姓算法
#include<cstdio>
#include<cstring>
const int MAXN=1e5+10,INF=1e8+10;
using namespace std;
inline char nc()
{
static char buf[MAXN],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin)),p1==p2?EOF:*p1++;
}
inline int read()
{
char c=nc();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();}
return x*f;
}
int dp[3001][3001],sum[MAXN],s[3001][3001];
int main()
{
#ifdef WIN32
freopen("a.in","r",stdin);
#else
#endif
int N=read();
for(int i=1;i<=N;i++) sum[i]=read(),sum[i]+=sum[i-1],s[i][i]=i;
for(int i=N;i>=1;i--)
{
for(int j=i+1;j<=N;j++)
{
int mn=INF,mnpos=0;
for(int k=s[i][j-1];k<=s[i+1][j];k++)
{
if(dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1] < mn)
{
mn=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1];
mnpos=k;
}
}
dp[i][j]=mn;
s[i][j]=mnpos;
}
}
printf("%d",dp[1][N]);
return 0;
}
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


