未名湖的烦恼-回溯，动态规划

问题描述 

　　每年冬天，北大未名湖上都是滑冰的好地方。北大体育组准备了许多冰鞋，可是人太多了，每天下午收工后，常常一双冰鞋都不剩。 
　　每天早上，租鞋窗口都会排起长龙，假设有还鞋的m个，有需要租鞋的n个。现在的问题是，这些人有多少种排法，可以避免出现体育组没有冰鞋可租的尴尬场面。（两个同样需求的人（比如都是租鞋或都是还鞋）交换位置是同一种排法） 
输入格式 
　　两个整数，表示m和n 
输出格式 
　　一个整数，表示队伍的排法的方案数。 
样例输入 
3 2 
样例输出 
5 
数据规模和约定 

　　m,n∈［0,18］ 

 

题解 回溯：构造一个二叉树，得到排列完所有人的情况，结果++,最后输出结果。

样例输入中的3 2，会产生下面的树，没有画图工具大家凑合一下。其中1代表送鞋的，0代表租鞋的。

 

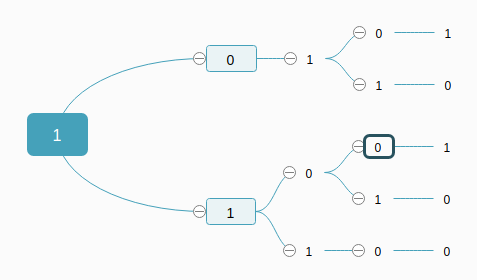
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int now=0;//当前冰鞋
int res;//人数
int k=0;
void rank(int m,int n){
    if(m==0&&n==0)
        res++;
    if(now>0){
        if(n>0)
            --now,rank(m,n-1),now++;    //回溯
        if(m>0)
            ++now,rank(m-1,n),now--;
    }else
        if(m>0)
            ++now,rank(m-1,n),now--;
}

int main(){
    int m,n;
    freopen("a.txt","r",stdin);
    scanf("%d %d",&m,&n);
    if(m<n){
        printf("%d",0);return 0;}
    if(n==0){
        printf("%d",1);return 0;}
    rank(m,n);
    printf("%d",res);
    return 0;
}

题解 动态规划：

当i=j时，dp[i][j]=dp[i][j-1] 

当i>j时，当前位置随便放借鞋还是还鞋都可以, dp[i][j]=dp[i-1][j-1]+dp[i][j-1]

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
using namespace std;
int dp[25][25];
int main()
{
    int m, n;
    scanf("%d%d",&m,&n);
    memset(dp,0,sizeof(dp));
    for (int i = 1; i <= m; i++){
        dp[i][0] = 1;
    }
    for (int i = 1; i <= m; i++){
        for (int j = 1; j <= n; j++){
            if (i == j){
                dp[i][j] = dp[i][j - 1];
            }
            if (i>j){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    printf("%d\n",dp[m][n]);
    return 0;
}

今天在这道题上浪费了不少时间，所以记录一下。