学习子句集管理——文献学习Simplifying CDCL Clause Database Reduction

Jamali S., Mitchell D. (2019) Simplifying CDCL Clause Database Reduction. In: Janota M., Lynce I. (eds) Theory and Applications of Satisfiability Testing – SAT 2019. SAT 2019. Lecture Notes in Computer Science, vol 11628. Springer, Cham

Simplifying CDCL Clause Database Reduction

---

Abstract

CDCL SAT solvers generate many “learned” clauses, so effective clause database reduction strategies are important to performance. Over time reduction strategies have become complex, increasing the difficulty of evaluating particular factors or introducing new refinements. 译文：随着时间的推移，减少的战略变得复杂，增加了评估特定因素或引入新的改进的难度。At the same time, it has been unclear if the complexity is necessary. We introduce a simple online clause reduction scheme, which involves no sorting.译文：与此同时，还不清楚这种复杂性是否有必要。我们引入了一个简单的在线子句缩减方案，它不涉及排序。 We instantiate this scheme with simple mechanisms for taking into account clause activity and LBD within the winning solver from the 2018 SAT Solver Competition, obtaining performance comparable to the original.译文：我们用简单的机制实例化了这个方案，将子句活动和LBD考虑到2018年SAT求解器竞赛的胜出求解器中，获得了与原方案相当的性能 。We also present empirical data on the effects of simple measures of clause age, activity and LBD on performance.译文：我们还提供了关于条款年龄、活动和LBD等简单措施对性能影响的经验数据。

Keywords

Clause deletion CDCL Clause database reduction 

 

 

1 Introduction

CDCL SAT solvers generate a very large number of new “learned” clauses, so clause management methods are central to solver performance [2, 13]. In particular, most learned clauses must be deleted to keep the clause database of practical size, and the clause database reduction scheme is one of a small number of key heuristic mechanisms in a CDCL solver [3, 14]. Typical clause maintenance strategies involve two stores of learned clauses, which we will call Core and Local. Clauses placed in Core are retained for the entire run. The size of Core is limited by being selective about which clauses are added. The large majority of learned clauses are placed in Local. The size of Local is limited by periodic deletion of “low quality” clauses, which are deemed unlikely to be of high future utility. The quality measure is typically a combination of size, age, literal block distance (LBD) and some measure of usage or activity [3, 8, 9, 10, 11, 14, 15].

译文：特别是，为了使子句数据库保持实际规模，必须删除大多数学习子句，子句数据库约简方案是CDCL求解器中少数关键启发式机制之一[3,14]。译文：典型的子句维护策略包括两种已学习子句的存储，我们称之为核心存储和局部存储。放置在Core中的子句将在整个运行期间保留。通过选择性地添加哪些子句来限制核心的大小。译文：绝大多数习得的子句都是局部的。Local的规模受到定期删除“低质量”子句的限制，这些子句被认为不太可能有很高的未来效用。译文：质量度量通常是大小、年龄、文字块距离(LBD)和一些使用或活动度量的结合。

Major changes to the general scheme are rare, but over time many refinements have combined to make the overall mechanism in the best recent solvers quite complex. Most details have intuitive explanations, and were chosen based on empirical performance. At the same time, the complexity seems perhaps a bit much relative to our understanding of “clause quality”. This complexity makes it hard to evaluate the contributions of individual elements, and is an obstacle to adding new features or refined quality measures.

译文：对一般方案的重大更改很少，但随着时间的推移，许多改进结合在一起，使得最近最好的解决方案中的总体机制相当复杂。译文：大多数细节都有直观的解释，并且是根据实证绩效来选择的。译文：与此同时，这种复杂性似乎与我们对“子句质量”的理解有一定的关系。译文：这种复杂性使得评估单个元素的贡献变得困难，并且成为添加新特性或改进质量度量的障碍。

There are two main aspects to a clause deletion strategy. The first is a method to categorize clauses as likely to be useful (high quality), or not (low quality). The second is implementation of an algorithmic method to remove low quality clauses efficiently. In an idealized scheme, we might have a clause quality measure Q, and keep the clauses in a heap so that the lowest quality clause(s) can be removed when the clause database is deemed too large. Conventional wisdom is that using a heap would be too inefficient. It also seems unlikely that spending time to obtain the very worst clause is necessary. Thus, fast heuristics are desired. One scheme, which we call Delete-Half, is to periodically sort the clauses of Local and delete the half with lowest quality. This scheme has been very widely used for many years, but there are many other possible schemes. While some solvers use other schemes (e.g., [4, 16]), we think much more investigation is justified. Regarding clause quality, we expect a very good clause quality measure to involve a combination of many factors. The dominant current quality measure uses VSIDS-like clause “activities”. Unfortunately, the way activities are computed and maintained in practice makes it hard to combine activity with other measures of quality in a simple and meaningful way.

译文：子句删除策略有两个主要方面。第一个方面是设法将子句分类为有用的(高质量)或无用的(低质量)。译文：第二方面是实现一种有效去除低质量子句的算法方法。译文：在理想的模式中，我们可能有一个子句质量度量Q，并将子句保存在堆中，以便在子句数据库被认为太大时可以删除质量最低的子句。译文：传统观点认为，使用堆效率太低。译文：似乎也不太可能花费时间来获得最坏条款是必要的。因此，快速启发式是需要的。一种我们称为delete - half的方案是周期性地对Local的子句进行排序，然后删除质量最低的那一半。译文：该方案已广泛使用多年，但还有许多其他可能的方案。当一些解决方案使用其他方案(例如，[4,16])，我们认为更多的调查是合理的。我们期望一个非常好的子句质量措施涉及到许多因素的结合。目前占主导地位的质量度量使用类似vsid的子句“活跃度”。不幸的是，在实践中计算和维护活跃度的方式使得很难以简单而有意义的方式将活跃度与其他质量度量结合起来。

 

The goal of this work is to identify simple methods that might largely account for effectiveness of the best current schemes. We make the following contributions.译文：这项工作的目标是找出能够在很大程度上解释当前最佳方案有效性的简单方法。我们做出以下贡献：

1. We introduce a new “online” clause deletion scheme which is simple to implement and maintains the size of Local at a desired value. It does not use sorting and in many natural instantiations takes constant time per conflict. The scheme is presented in Sect. 2.

   译文：我们引入了一种新的“online”子句删除方案，该方案易于实现并将本地子句的大小保持在一个期望的值。它不使用排序，而且在许多自然实例化中，每次冲突花费的时间都是常量。该方案在第2节中介绍。 

2. We show that a simple instantiation of this scheme performs comparably to the state of the art. In particular, we implemented the scheme within MapleLCMDistChronoBT, the first-place solver from the 2018 SAT Competition [1, 12]. This instantiation takes into account clause usage and LBD using very simple mechanisms. The resulting solver (Online-RU-T2Flag) and its performance are described in Sect. 4.

    译文：我们展示了该方案的一个简单实例，其执行情况与当前的技术水平相当。特别是，我们在MapleLCMDistChronoBT中实现了该方案，MapleLCMDistChronoBT是2018年SAT竞赛的第一名求解器[1,12]。这个实例化考虑了子句使用和LBD使用非常简单的机制。所得到的求解器(Online-RU-T2Flag)及其性能将在第4节中描述

3. To aid in understanding the degree to which the particular methods play a role in solver performance, we present data from a number of experiments measuring performance or other properties. These appear throughout remaining sections.

   译文：为了帮助理解特定方法对求解器性能的影响程度，我们提供了一些测量性能或其他性能的实验数据。这些内容将贯穿其余部分。

Our performance evaluations are carried out using the 400 formulas from the main track of the 2018 SAT Solver Competition, with a 5000 second cut off. Our baseline solver for performance evaluation is MapleLCMDistChronoBT, winner of the competition and all other solvers are modified versions of it. The computations were performed on the Cedar compute cluster [6] on 32-core, 128 GB nodes with Intel “Broadwell” CPUs running at 2.1 Ghz.

1.1 MapleLCMDistChronoBT Clause Database Management

Many top-performing solvers in recent SAT Solver Competitions have been variants or derivatives of MapleSAT [11]. For simplicity, we focus on the first-place solver from the 2018 competition, MapleLCMDistChronoBT [12], which uses the deletion scheme introduced in COMiniSatPS [14, 15].

译文：许多在最近的SAT求解器比赛中表现最好的求解器是MapleSAT[11]的变种或衍生品。为简单起见，我们重点关注2018年比赛的第一名，MapleLCMDistChronoBT[12]，它使用COMiniSatPS中引入的删除方案[14,15]。

This scheme has three clause databases, called Core, Tier2 and Local. The decision of where to store a newly learned clause in is based on its LBD: Core if LBD≤3, Tier2 if 4≤LBD≤6 and Local if 6<LBD. If after 100,000 conflicts there are not enough clauses in Core, the core threshold is changed from 3 to 5. A clause may be moved from one DB to another based on LBD or usage. The LBD of each clause is recomputed whenever it is used in conflict analysis or the clause simplifying procedure [3]. If the LBD of a clause is sufficiently reduced, it is moved from Local to Tier2 or Core, or from Tier2 to Core. Every 10,000 conflicts, every clause in Tier2 that has not been used during the last 30,000 conflicts is moved to Local. Every 15,000 conflicts, all the clauses in Local are sorted by their activity and MapleLCMDistChronoBT deletes half of the clauses with lower activities. Clauses that are a reason for a current assignment and clauses with recent improvement in LBD are saved from deletion [3, 14].

译文：一个子句可以根据LBD或使用从一个DB移动到另一个DB。译文：每当在冲突分析或子句简化过程[3]中使用它时，都会重新计算每个子句的LBD。译文：如果一个子句的LBD被充分减少，那么它将从本地转移到Tier2或核心，或者从Tier2转移到核心。译文：每10,000个冲突，Tier2中在最近30,000个冲突中未使用的每个子句都被转移到本地。每15000起冲突，Local中的所有子句都按照活动进行排序，MapleLCMDistChronoBT删除一半活动较低的子句。译文：作为当前分配原因的子句和LBD中最近改进的子句被保存起来，以免被删除[3,14]。

 

2 Online Clause Deletion

子句管理的在线删除方法：

　　Local的子句在循环列表L中维护，索引变量i按一个方向遍历列表。索引标识当前的“删除候选”L_i。

　　我们有一个子句质量度量Q，和一些阈值质量值Q。当一个新的学习过的子句C需要存储在本地时，我们选择列表中的一个“低质量”子句，通过顺序搜索将其替换为C。

　　As long as Q(L_i)≥q, we increment i (“saving” clause L_i for one more “round”); The first time Q(L_i)<q, we replace L_i with C (deleting the “old” L_i). 

　　必须选择子句质量度量阈值，以便列表中始终有足够多的“低质量”子句。译文：有一些算法方法来确保这一点(例如，使用反馈控制机制)，但没有它们也不难获得良好的实际性能。

Relating Delete-Half and Online Deletion. 

　　 Consider a Delete-Half scheme with a sort-and-reduce phase every k conflicts. Roughly speaking (ignoring some details for simplicity) each clause is inspected every k conflicts, deleted if its quality is below the median of the current clauses in Local.译文：每k个冲突对每个子句进行检查，如果其质量低于当前子句在Local中的中值则予以删除。 If we instantiate our online scheme with S=2k, and keep q sufficiently close to the median, we expect each clause to be inspected every k conflicts and deleted if its quality is below the median of the current clauses in Local. 译文：如果我们实例化我们的在线方案，S=2k，并且q足够接近中值，我们期望每个子句在每k个冲突中都被检查，如果它的质量在局部小于当前子句的中值，就会被删除。In this sense, the two schemes can be made quite close: we trade off sorting for dynamically estimating the median. 译文：从这个意义上说，这两种方案可以非常接近:我们用动态估计中值来交换排序。In doing so, we get a clause database of uniform size, rather than one that significantly grows and shrinks.译文：这样，我们就得到了一个大小一致的子句数据库，而不是一个显著增大或缩小的子句数据库。

Age-Based Deletion.——注释：如果每个子句都小于q时，考虑age，用new代替old。

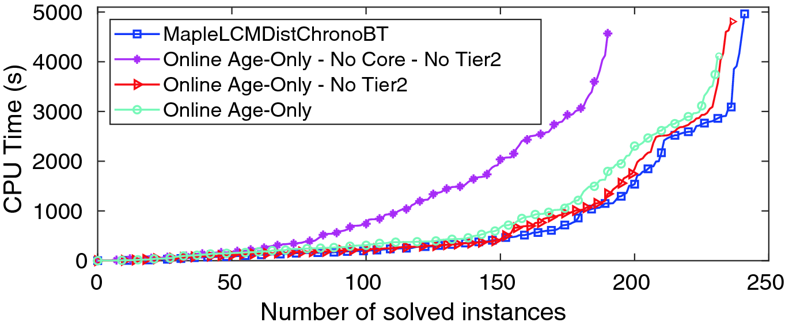
 A trivially implemented version of our scheme assumes Q(C)<q for every clause C. This results in a pure age-based scheme: Each new learned clause replaces the oldest clause in Local. This very low-cost scheme works surprisingly well. Figure 1 shows a “cactus-plot” comparison of default MapleLCMDistChronoBT with 3 variants using online deletion. (The Local size limit is set to 80,000 clauses in all solvers using online deletion reported here.)

译文：我们的方案的一个普通实现版本假设每个子句C都有Q(C)< q。

Fig. 1.

Simple online deletion performance.

• Online Age-Only - No Core, No Tier2. This has no permanent store at all, just pure age-based deletion of all learned clauses.

• Online Age-Only - No Tier2. This version keeps clauses with LBD ≤3 or Size ≤4 permanently in Core, and uses pure age-based deletion from Local.

• Online Age-Only. In this version we use Core and Tier2 just as in MapleLCMDistChronoBT, but use age-based online deletion from Local. If a clause is moved from Tier2 to Local, it replaces the oldest clause in Local.

Figure 1 shows that Core and Tier2 are important to the performance of MapleLCMDistChronoBT. It also shows that in the presence of Core and Tier2 a simple pure age-based deletion scheme for Local gives quite good performance.

We make two observations regarding this second point. First, in online deletion with Local of size S, if the probability of saving a clause is as most 0.5 (see Fig. 4), then every learned clause is kept for at least S / 2 conflicts, giving it substantial time to be used. Delete-Half schemes generally do not ensure this. Second, age is highly correlated with usage rate, and can account for a large fraction of decisions that would be made based on clause activities. This is illustrated by Fig. 2, which shows the average usage rates of clauses that have been in Local for at least 10K conflicts, at different ages. The usage rate of most clauses drops very quickly.

 

3 Clause Usage

MiniSAT and many of its successors, including MapleLCMDistChronoBT, use clause “activity” scores in their clause deletion schemes [8, 11, 15]. If a clause is used in conflict analysis, its activity is “bumped”, meaning it’s activity score is increased by a reward value. The reward is initialized to 1 and divided by 0.999 (the decay factor) at each conflict, to similate decay of activities. To prevent activity overflow, when the activity of any clause reaches 1e20, all activity values and the reward value are divided by 1e−20 [5, 8].

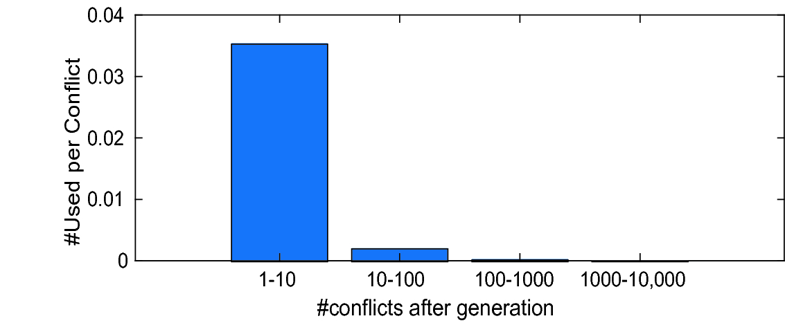Fig. 2.

Rate of use of clauses in Local at different ages.

This scheme, with many variations, has been widely used, but it also has inconvenient aspects as discussed above. We anticipated that, in the presence of Core, much simpler usage measures might be effective. Here we report two that we have considered. Both are extremely simple to implement. We follow their descriptions with reports of three experiments that may shed light on the performance of the RU measures.

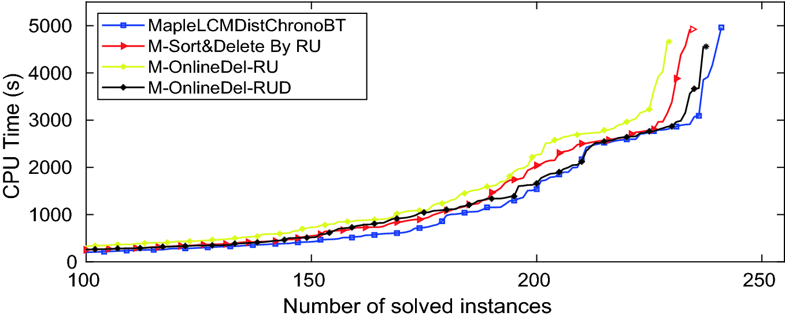Fig. 3.

Online deletion with recent usage

M-OnlineDel-RU.   M-OnlineDel-RUD

• M-OnlineDel-RU。In this version, the measure Q of quality (or activity) is just the number of times the clause was used in conflict analysis during the last “round”. That is, we count uses and reset the count to zero if the clause becomes the candidate for deletion but is saved. We denote this measure RU, for Recently-Used. If the threshold value is q (denoted RU=qRU=q), a clause will be saved if it was used q or more times in the last round.

• M-OnlineDel-RUD. This is similar to M-OnlineDel-RU, but instead of resetting RU to 0 when a clause is saved, we decay it by dividing it by a constant. We call this measure RUD.

Figure 3 shows the performance of M-OnlineDel-RU with threshold RU = 2 and M-OnlineDel-RUD with RU = 2 and Decay constant 4. Both versions perform quite well, the decay version being almost as good as MapleLCMDistChronoBT. This suggests that online deletion using simple measures might compete effectively with Delete-Half using traditional activities.

To understand the effectiveness of RU versus traditional activities, we created a solver M-Sort&Delete By RU that is identical to MapleLCMDistChronoBT but does sorting and deletion from Local based on RU instead of activity. Figure 3 shows the performance is slightly inferior to MapleLCMDistChronoBT on our benchmark, lying between the performance of the two versions with online deletion. This suggests that we pay no penalty for using online deletion instead of the Delete-Half scheme, and confirms that in the presence of Core and Tier2 a simple usage measure can be almost as useful as traditional clause activities.

Fig. 4.

Fraction of saved clauses in different online deletion schemes (Color figure online)

Fraction Saved by RU.

Here we examine the fraction of clauses in Local that become candidates for deletion but are saved based on the RU measure. Figure 4 shows this value for several variations. In each pair of bars, the right bar (orange) shows the fraction of clauses with RU≥q; the left bar (blue) shows the fraction of clauses saved based on either RU or because of being “locked” [8].

With q=1, the probability of deletion is less than 1/2, and the performance of the solver is poor.

In contrast, with q=2, about three quarters of clauses are deleted, and the performance is quite good as shown in Fig. 3. In the remainder of the paper, all solvers using RU have q is set to 2.

Table 1.

Commonality among high-activity clauses and recently-used clauses.

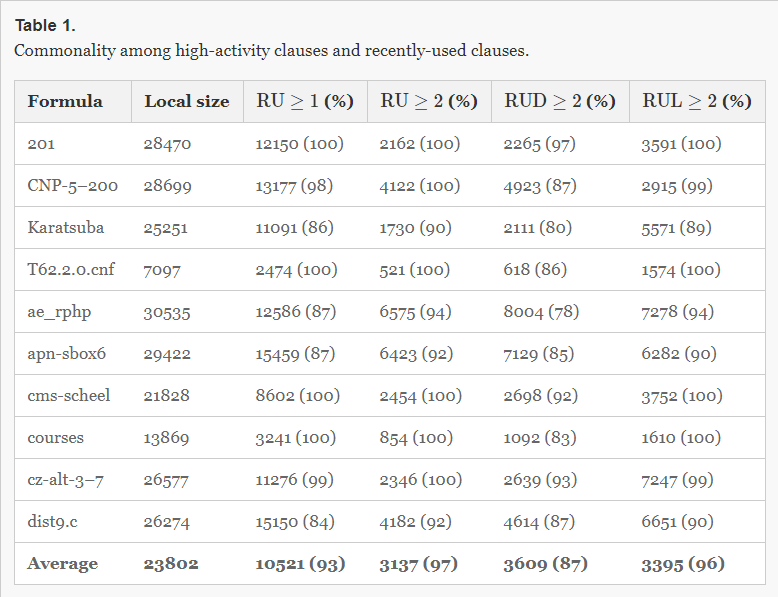Clauses Saved by RU and Activity. We examined the clauses in Local just before the 10thth clause deletion in MapleLCMDistChronoBT, and measured their RU and activity values to see what fraction of clauses would be saved by our RU-based schemes. Table 1 shows the results for one formula from each of 10 families. The first column is the number of clauses in Local just before deletion. Other columns show the number of clauses that would be saved due to RU≥q, and the fraction (in percent) of these clauses that have high enough activity to be saved by Delete-Half. On average this fraction is between 87 and 97%, suggesting that simple RU counters can account for a significant fraction of decisions based on activities.

Fig. 5.

Online deletion with usage and LBD

 

4 Clause LBD and Tier2

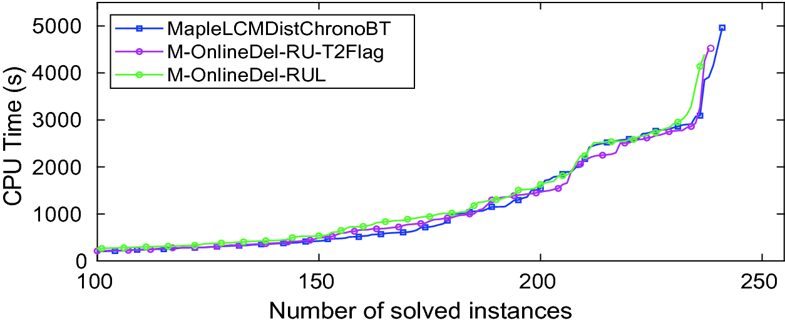
LBD is used in MapleLCMDistChronoBT for initial placement of a learned clause, and to move clauses between stores if the LBD changes. Here we report two simple methods to take into account LBD changes in a solver with online deletion and no Tier2. Figure 5 show the resulting performance.

M-OnlineDel-RU-T2Flag. 

Here we replace Tier2 with a rough simulation, by adding a “Tier 2 flag” to clauses in Local. We set the flag true if MapleLCMDistChronoBT would move it from Local to Tier2, and false for the reverse direction. Clauses with this flag true are always saved. This is not an accurate Tier2 simulation, because the size of the clause DB does not change appropriately. Nonetheless, the resulting performance is very close to the original solver.

M-OnlineDel-RUL.

Here we take LBD into account by modifying the usage scoring. Instead of incrementing RU by 1 each time a clause is used, we increment by c/LBD, for a constant c. We call this RUL, for RU with LBD. The RUL values are re-set to zero when a clause is saved. The curve in Fig. 5 is the performance with c=20.

Table 2.

Performance on satisfiable vs unsatisfiable formulas.

5 Discussion

We introduced a new, simple online clause deletion scheme, and reported the performance of instantiations of the scheme using clause age, LBD and very simple measures of usage. An implementation of the online scheme in MapleLCMDistChronoBT, the winning solver from the main track of the 2018 SAT Solver Competition, has performance almost as good as the original.译文：我们引入了一个新的、简单的在线子句删除方案，并使用子句年龄、LBD和非常简单的使用度量报告了方案实例化的性能。该在线方案在MapleLCMDistChronoBT中的实现，即2018年SAT求解器大赛主道的胜出求解器，性能几乎与原方案一样好。

Online deletion requires less computation time than the Delete-Half scheme. However, the fraction of run time consumed by deletion in MapleLCMDistChronoBT is small, so this is not a major performance factor.译文：在线删除比半删除模式需要更少的计算时间。但是，在MapleLCMDistChronoBT中，删除操作占用的运行时间很小，所以这不是主要的性能因素。

The online deletion schemes in this paper use age or age modified by a fixed quality threshold. A dynamic threshold may be more desirable, in which case we may use a feedback control scheme to ensure the threshold is such that the fraction of saved clauses is suitable (cf Fig. 4).译文：本文的在线删除方案使用年龄或年龄经过一个固定的质量阈值修改。动态阈值可能更理想，在这种情况下，我们可以使用反馈控制方案来确保阈值是这样的，即保存子句的比例是合适的(参见图4)。

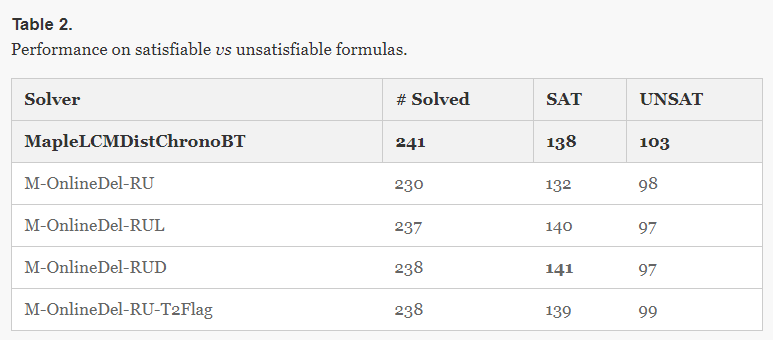
We continue to investigate more refined versions of our scheme, in particular with regard to clause quality measures and clause database size. Table 2 shows that our modified solvers are biased toward Satisfiable instances, and we will work on shifting this bias.译文：我们将继续研究我们方案的更精细版本，特别是子句质量度量和子句数据库大小。表2显示了修改后的求解器偏向于可满足的实例，我们将努力改变这种偏向。

 

 

 

References

1.

The international SAT competitions web page. https://www-satcompetition-org-s.era.lib.swjtu.edu.cn:443

2.

Ansótegui, C., Giráldez-Cru, J., Levy, J., Simon, L.: Using community structure to detect relevant learnt clauses. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 238–254. Springer, Cham (2015).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-24318-4_18CrossRefGoogle Scholar

3.

Audemard, G., Simon, L.: Predicting learnt clauses quality in modern SAT solvers. In: Proceedings of the 21st International Jiont Conference on Artificial Intelligence, IJCAI 2009, pp. 399–404. Morgan Kaufmann Publishers Inc., San Francisco (2009)Google Scholar

4.

Biere, A.: Pre, icosat@sc’09. solver description for SAT competition 2009. SAT Competitive Event Booklet (2009)Google Scholar

5.

Biere, A., Fröhlich, A.: Evaluating CDCL Variable scoring schemes. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 405–422. Springer, Cham (2015).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-24318-4_29CrossRefGoogle Scholar

6.

Cedar, A Compute Canada Cluster. https://docs.computecanada.ca/wiki/Cedar

7.

Compute Canada: Advanced Research Computing (ARC) Systems. https://www.computecanada.ca/

8.

Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-540-24605-3_37CrossRefGoogle Scholar

9.

Goldberg, E., Novikov, Y.: BerkMin: A fast and robust SAT-solver. In: Lauwereins, R., Madsen, J. (eds.) Design, Automation, and Test in Europe, pp. 465–478. Springer, Dordrecht (2008).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-1-4020-6488-3_34CrossRefGoogle Scholar

10.

Jamali, S., Mitchell, D.: Centrality-based improvements to CDCL heuristics. In: Beyersdorff, O., Wintersteiger, C.M. (eds.) SAT 2018. LNCS, vol. 10929, pp. 122–131. Springer, Cham (2018).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-94144-8_8CrossRefGoogle Scholar

11.

Liang, J.H., Ganesh, V., Poupart, P., Czarnecki, K.: Learning rate based branching heuristic for SAT solvers. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 123–140. Springer, Cham (2016).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-40970-2_9CrossRefzbMATHGoogle Scholar

12.

Nadel, A., Ryvchin, V.: Chronological backtracking. In: Beyersdorff, O., Wintersteiger, C.M. (eds.) SAT 2018. LNCS, vol. 10929, pp. 111–121. Springer, Cham (2018).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-94144-8_7CrossRefGoogle Scholar

13.

Newsham, Z., Ganesh, V., Fischmeister, S., Audemard, G., Simon, L.: Impact of community structure on SAT solver performance. In: Sinz, C., Egly, U. (eds.) SAT 2014. LNCS, vol. 8561, pp. 252–268. Springer, Cham (2014).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-09284-3_20CrossRefzbMATHGoogle Scholar

14.

Oh, C.: Between SAT and UNSAT: the fundamental difference in CDCL SAT. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 307–323. Springer, Cham (2015).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-24318-4_23CrossRefGoogle Scholar

15.

Oh, C.: Improving SAT solvers by exploiting empirical characteristics of CDCL. Ph.D. thesis, New York University (2016)Google Scholar

16.

Soos, M., Nohl, K., Castelluccia, C.: Extending SAT solvers to cryptographic problems. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 244–257. Springer, Heidelberg (2009).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-642-02777-2_24CrossRefGoogle Scholar