AGC039 题解
[AGC039A] Connection and Disconnection
题意
给定字符串 \(S\) 和正整数 \(k\),令 \(T\) 为 \(k\) 份 \(S\) 后拼接的结果,输出使 \(T\) 任意相邻字符不相等的最小操作数。
idea
对于一段长为 \(n\) 的连续相同字符,最小操作次数是 \(\left\lfloor\frac{n}{2}\right\rfloor\)。
于是可以把相同的一段缩成一个字符。注意到 \(i\in[2,m-1]\) 的位置贡献保持不变,直接计算乘 \(k\) 即可。
而首尾拼接后,如果 \(a_1=a_m\) 可能需要多删,于是把尾首拼接后视作一段,总共 \(k-1\) 段,再加上 \(T\) 开头和结尾的贡献即可。如果 \(a_1\neq a_m\) ,则照常计算即可。
特别的,如果 \(m=1\),即所有字符相同,答案是 \(\left\lfloor\frac{nk}{2}\right\rfloor\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define N 200005
#define endl "\n"
#define fi first
#define se second
using namespace std;
const ll mod=1e9+7;
const ll inf=1e18;
const double eps=1e-6;
string s;
ll n,k,m;
ll a[N],val[N];
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>s>>k;
n=s.size();
s=" "+s;
for(int i=1;i<=n;i++){
if(a[m]!=s[i]-'a'+1)a[++m]=s[i]-'a'+1;
val[m]++;
}
ll res=val[1]/2+val[m]/2;;
for(int i=2;i<m;i++)res+=val[i]/2*k;
if(a[1]==a[m])res+=(val[1]+val[m])/2*(k-1);
else res+=(val[1]/2+val[m]/2)*(k-1);
if(m==1)res=val[1]*k/2;
cout<<res<<endl;
return 0;
}
[AGC039B] Graph Partition
题意
给定 \(n\) 个点 \(m\) 条边的无向连通图。请判断是否能够将顶点分为 \(k\) 个非空集合 \(V_1,\ldots,V_k\),使得其满足以下条件。若可以,则最大化 \(k\):
- 对于每条边 \((i,j)\),存在 \(1 \le t \le k-1\) 满足 \(i \in V_t, j \in V_{t+1}\) 或 \(i \in V_{t+1}, j \in V_t\)。
\(n\le 200\)
idea
如果是最小化,就是简单的二分图黑白染色,可以先把无解判了。
注意到 \(n\) 很小,考虑跑全局最短路,答案是 \(\max\limits_{1\le i,j\le n} dis(i,j)\) 。
根据最短路的性质,路径上所有点之间所属集合恰好相差 \(1\),所以符合题意。
总结
- 重要观察:划分集合的方式与跑最短路类似。
Code
#include<bits/stdc++.h>
#define ll long long
#define N 2005
#define endl "\n"
#define fi first
#define se second
using namespace std;
const ll mod=1e9+7;
const ll inf=1e18;
const double eps=1e-6;
ll n;
ll a[N][N];
vector<ll>v[N];
ll col[N];
queue<ll>q;
ll bfs(ll x){
for(int i=1;i<=n;i++)col[i]=0;
col[x]=1;
q.push(x);
ll ans=0;
while(!q.empty()){
auto t=q.front();
q.pop();
ans=max(ans,col[t]);
for(auto y:v[t]){
if(!col[y]){
col[y]=col[t]+1;
q.push(y);
continue;
}
if((col[y]&1)!=(col[t]&1^1))return inf;
}
}
return ans;
}
string s;
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++){
cin>>s;
s=" "+s;
for(int j=1;j<=n;j++)if(s[j]-'0')v[i].push_back(j);
}
ll res=0;
for(int i=1;i<=n;i++)res=max(res,bfs(i));
if(res==inf)res=-1;
cout<<res<<endl;
return 0;
}
[AGC039C] Division by Two with Something
题意
现在给你一个整数 \(N\) 和一个二进制数 \(p\),对 \(0 \sim p\) 之间的每个整数 \(x\) 在返回到其原始值之前,需要执行多少次下面的操作:
如果 \(x\) 是奇数:\(x=(x-1) \div 2\)
如果 \(x\) 是偶数:\(x=(x \div 2)+2^{N-1}\)
idea
除了暴力没有思路。
Sol
发现操作相当于每次把最后一位取反后移到最高位,所以最多 \(2n\) 次。
考虑模拟这个操作,相当于把 \(x\) 和 \(\neg x\) 拼接,设为 \(y\),\(x\) 复原相等于 \(y\) 的前 \(n\) 位复原,也就是 \(y\) 复原。
于是考虑找循环节,使得每 \(t\) 次令 \(y\) 复原一次,则 \(t|2n\)。但是如果 \(t|n\),那么前 \(n\) 位和后 \(n\) 位相等,不满足 \(x\) 和 \(\neg x\) 拼接。
对于一个合法的 \(t\) ,容易发现一定有 \(2|t\),且 \(\frac{2n}{t} \equiv 1 \pmod 2\),把其分成两部分 \(a,b\),于是最终二进制数一定是: $y=\overline{ababa\cdots bab} \(,\)x=\overline{abab\cdots a}$ 与 $\neg x=\overline{baba\cdots ab} $ 的形式,注意到 \(a=\neg b\),于是我们只需要知道前 \(\frac{t}{2}\) 位,整个二进制数便确定下来了。
考虑 \([0,p]\) 的限制,我们令 \(a\) 成为 \(x\) 的前缀,仿照 \(x=\overline{abab\cdots a}\) 的构造方式构造长为 \(n\) 的二进制数 \(q\),并判断与 \(p\) 的大小关系,记 \(f_t\) 表示循环节长度为 \(t\) 合法数字数量。
-
\(p\ge q\) :前 \(\frac{t}{2}\) 位填十进制下 \([0,a]\) 的数都合法,于是\(f_t=s+1\)。
-
\(p<q\) : 由于前 \(\frac{t}{2}\) 位与 \(p\) 一致,那么一定是后面产生了问题,那么填 \([0,a-1]\) 的数即可满足 \(p>q\),于是 \(f_t=s\)。
但是这样还不对,若存在合法 \(t\) 与 \(T\) 满足 \(t |T\) ,那么 \(t\) 被多算了几遍,于是我们进行容斥,枚举倍数减去贡献:
总结
- 喵喵题。
- 重要观察 \(1\):操作相当于每次把最后一位取反后移到最高位
- 重要观察 \(2\):\(x=\overline{abab\cdots a}\) 与 $\neg x=\overline{baba\cdots ab} $ ,\(a=\neg b\) 的构造方式。
Code
#include<bits/stdc++.h>
#define ll long long
#define N 20000005
#define endl "\n"
#define fi first
#define se second
using namespace std;
const ll mod=998244353;
const ll inf=1e18;
const double eps=1e-6;
ll n;
string s;
ll a[N],b[N],f[N];
vector<ll>t;
bool check(ll y){
for(int i=1,j=1;i<=n;i++,j=j%y+1){
if(b[j]==a[i])continue;
if(b[j]>a[i])return 0;
if(b[j]<a[i])return 1;
}
return 1;
}
ll fpow(ll x,ll y){
ll res=1;
while(y){
if(y&1)res=res*x%mod;
x=x*x%mod;
y>>=1;
}
return res;
}
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>s;
s=" "+s;
for(int i=1;i<=n;i++)a[i]=s[i]-'0';
for(int i=1;i<=2*n;i++){
if(2*n%i!=0)continue;
if(n%i==0)continue;
t.push_back(i);
if(n%(2*n/i)!=0&&2*n!=i*i)t.push_back(2*n/i);
}
ll res=0;
sort(t.begin(),t.end());
for(auto y:t){
ll sum=0;
for(int i=1;i*2<=y;i++){
b[i]=a[i];
sum=(sum+a[i]*fpow(2,y/2-i)%mod)%mod;
}
for(int i=y/2+1;i<=y;i++)b[i]=a[i-y/2]^1;
if(check(y))f[y]=(f[y]+sum+1)%mod;
else f[y]=(f[y]+sum)%mod;
for(int i=2;i*y<=2*n;i++)f[i*y]=(f[i*y]-f[y]+mod+mod)%mod;
res=(res+f[y]*y%mod)%mod;
}
cout<<res<<endl;
return 0;
}
[AGC039D] Incenters
题意
给定 \(n\) 个单位圆上的点,等概率的随机选三个点组成三角形,求其内心坐标的期望值。
\(n\le 3000\)。
idea
注意到只需要求 \(\binom{n}{3}\) 种情况的内心坐标值之和即可。内心是不好求的,大抵是要转化成其它东西,可是不会。
Sol
高中必修二题。
定理 \(1\) :取外接圆上 \(\stackrel\frown{AB}\),\(\stackrel\frown{BC}\),\(\stackrel\frown{CA}\),中点 \(D,E,F\),\(\triangle DEF\) 的垂心是 \(\triangle ABC\) 的内心。
公式 \(1\) :若 \(O\) 是外心,\(H\) 是垂心,则有 $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} $
公式 \(2\) :若 \(O\) 是任意一点,\(G\) 是重心,则有 $3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} $
于是相当于是求 \(D_x+E_x+F_x\) 和 \(D_y+E_y+F_y\)。
记 \(2a_i=\frac{2\pi T_i}{L}\),表示出弧中点坐标:
考虑化简:
\[res1=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n\sum\limits_{k=j+1}^n \cos(a_i+a_j)=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n (n-j)\times \cos(a_i+a_j) \]
\[res2=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n\sum\limits_{k=j+1}^n \cos(a_j+a_k)=\sum\limits_{j=1}^n\sum\limits_{k=j+1}^n (j-1)\times\cos(a_j+a_k)=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n (i-1)\times \cos(a_i+a_j) \]
\[res3=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n\sum\limits_{k=j+1}^n \cos(a_i+a_k)=\sum\limits_{i=1}^n\sum\limits_{k=i+1}^n (k-i-1)\times\cos(a_i+a_k)=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n (j-i-1)\times\cos(a_i+a_j) \]
于是:
这样就能 \(O(n^2)\) 计算答案了
总结
- 结论题。
- \(O(n^3)\) 变成 \(O(n^2)\) 借用了 \(\text{ChatGPT}\) 的力量推了很长时间。
Code
#include<bits/stdc++.h>
#define ll long long
#define dl double
#define N 200005
#define endl "\n"
#define fi first
#define se second
using namespace std;
const ll mod=1e9+7;
const ll inf=1e18;
const double eps=1e-6;
const double pi=acos(-1.0);
ll n,k;
dl a[N];
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>a[i];
dl resx=0,resy=0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
resx+=(cos(pi*(a[i]+a[j])/k)*(n-2*(j-i)));
resy+=(sin(pi*(a[i]+a[j])/k)*(n-2*(j-i)));
}
}
dl p=n*(n-1)*(n-2)/6;
printf("%.20lf %.20lf",resx/p,resy/p);
return 0;
}
[AGC039E] Pairing Points
题意
一个圆上 \(2n\) 个点,一些点之间有连线,给出连线的邻接矩阵 \(d_{i, j}\),保证不存在三线共点的情况。
保留其中 \(n\) 条线,使得每个点恰好连一条线,并且这 \(n\) 条线画出来后构成一棵树。
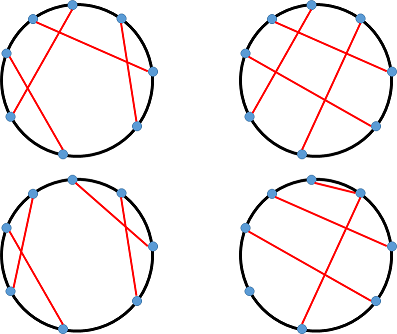
如图,左上角是合法的情况,右上角连出环了,左下角不是连通的,右下角不符合每个点恰好连一条线,请求出不同的连线方案的数量。
- \(1 \le n \le 20\)。
idea
题意很绕。
注意到连线后左右两部分贡献相对独立,猜测是分治,但是可能左右连线的不同情况导致合并区间很麻烦。
Sol
神仙题。
于是记 \(f(l,x,r)\) 表示在区间 \([l,x-1]\) 和 \([x+1,r]\) 中选一些点对相互连接,至少有一条跨过 \(x\),且这些直线互不相交。
首先记 \(n=2n\),即总共 \(2n\) 个点,由于每个点都要连线,所以钦定第一条的一端为 \(1\),另一端为 \(k\),将圆环分成了 \([2,k-1]\) 与 \([k+1,n]\) 两部分。
由于左右要求连通,所以必定至少有一条直线跨过直线 \((1,k)\),如果有多条,这些直线不能有交,否则会形成三元环,所以直线之间只能为包含关系。
于是我们的问题现在是求:在 \([2,k-1]\) 和 \([k+1,n]\) 中选一些点对相互连接,至少有一条跨过 \(k\),且这些直线互不相交的方案数。
考虑枚举最外层直线为 \((i,j)\), 那么从 \((i,j)\) 与 \((1,k)\) 的交点开始往圆环上走,根据第一次走到的端点分别为 \(i,x,j\) 分别占据了左,中,右三部分,考虑枚举 \(a\in[i+1,k-1],b\in[k,j-1]\) 作为分界点。
那么我们把 \([2,n]\) 分成了 \(i\in[2,a]\),\(k\in[a+1,b-1]\),\(j\in[b,n]\) 三部分,让每个部分内部通过与 \(i,x,j\) 分别连通(不能向外部连边),各个部分通过 \((i,j)\) 与 \((1,k)\) 相连。
每个部分变成了类似 区间 \([l,r]\) 被分成 \([l,x-1]\) 和 \([x+1,r]\) 两部分,
在左右区间中选一些点对相互连接,至少有一条跨过 \(x\),且这些直线互不相交的方案数。
这个东西和刚才所求的一模一样,于是可以记 \(f(l,x,r)\) 表示为这个部分的方案数,有转移方程:
边界状态:
最后我们的答案是:
时间复杂度 \(O(n^7)\),但是带一个\(\frac{1}{5040}\) 的常数,可以跑过。
总结
- 重要观察:转化子问题后动态规划: 设区间 \([l,r]\) 被分成 \([l,x-1]\) 和 \([x+1,r]\) 两部分,在左右区间中选一些点对相互连接,至少有一条跨过 \(x\),且这些直线互不相交的方案数为 \(f(l,r)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define N 200005
#define endl "\n"
#define fi first
#define se second
using namespace std;
const ll mod=1e9+7;
const ll inf=1e18;
const double eps=1e-6;
ll a[44][44];
ll n;
map<ll,ll>f[44][44];
ll dfs(ll l,ll x,ll r){
if(l==x&&x==r)return 1;
if(l==x||x==r)return 0;
if(f[l][r].count(x))return f[l][r][x];
ll res=0;
for(int i=l;i<x;i++){
for(int j=r;j>x;j--){
if(a[i][j]==0)continue;
for(int a=i;a<x;a++){
for(int b=x;b<j;b++){
res=(res+dfs(l,i,a)*dfs(a+1,x,b)*dfs(b+1,j,r));
}
}
}
}
return f[l][r][x]=res;
}
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n;
n*=2;
for(int i=1;i<=n;i++){
string s;
cin>>s;
for(int j=1;j<=n;j++)a[i][j]=s[j-1]-'0';
}
ll res=0;
for(int i=2;i<=n;i++){
if(a[1][i]==0)continue;
res=res+dfs(2,i,n);
}
cout<<res<<endl;
return 0;
}
[AGC039F] Min Product Sum
题意
- 有一个大小为 \(n \times m\) 的矩阵。矩阵中每个数的取值都是 \([1, k]\)。
- 对于一个矩阵,定义函数 \(f(x,y)\) 为:第 \(x\) 行和第 \(y\) 列的一共 \(n +m - 1\) 个数中的最小值。
- 对于一个矩阵,定义其权值为 \(\prod_{x=1}^{n}\prod_{y=1}^{m}f(x,y)\)。
- 你需要求出,对于所有 \(k^{nm}\) 种矩阵,每个矩阵的权值和对 \(d\) 取模的结果。
- \(1 \leq n, m, k \leq 100\),\(10^8 \leq d \leq 10^9\),保证 \(D\) 为质数。
idea
感觉和 [CTS2019] 随机立方体 很像。
注意到题目是求权值和,而权值只与行列最小值有关,说明不同矩阵可能权值相同,启示我们枚举一个权值计算合法方案数,考虑枚举这 \(n+m\) 个行列最小值,行最小值记作 \(a_i\),列最小值记作 \(b_i\)
于是一个矩阵的权值可以表示为:
计数部分,感觉不太会啊?猜测是逆天容斥。
而对于枚举 \(a_i,b_j\),也没有很好的方法可以快速计算。
Sol
看不懂小粉兔的题解,怎么绘世呢?
已知矩阵权值可以表示为:
计算对应图的数量,要求恰好行列最小值等于 \(a_i,b_i\),考虑容斥,统计钦定第 \(i\) 行第 \(j\) 列的最小值大于 \(a_i,b_i\),即此时取值范围为 \([\max(a_i,b_i)+1,k]\),对应的方案数为:
\(x_i,y_j\) 表示第 \(i\) 行第 \(j\) 列最小值是否大于 \(a_i,b_i\)。
于是总的方案权值和可以写成:
现在目标是快速计算以上的式子,考虑从小到大加入最小值 \(x\),设已经加入了 \(i\) 行,\(j\) 列,若加入的 \(x\) 是行最小值,现在只有 \(m-j\) 列的最小值为 \(x\),于是会贡献 \(x^{m-j}\),对于列则是贡献 \(x^{n-i}\)。每次枚举加入多少个 \(x\) 加入即可。
而对于已经确定的 \(i\) 个位置,其可以填 \([x,k]\) 范围内的任意值,贡献是 \((k-x+1)^{di}\),列同理,钦定大于的范围是 \([x+1,k]\)。
于是可以记 \(f[x][i][j]\) 表示从小到大的放入小于等于 \(x\) 的值,已经放了 \(i\) 行 \(j\) 列的方案权值之和。
考虑加入行不容斥的情况:
考虑加入列不容斥的情况:
考虑加入行容斥的情况:
考虑加入列容斥的情况:
答案是 \(f[k][n][m]\),其中 \(g[i][j]\) 为上一阶段的 dp 数组。
时间复杂度 \(O(nmk(n+m))\),需要预处理快速幂卡常。
鲜花
以下是官方做法的转移方程:
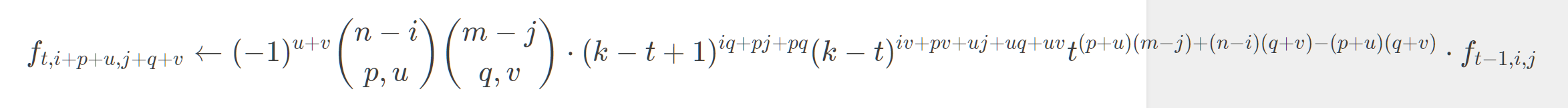
太哈人了。
总结
- dp 部分不太好想
- 把系数也放一起 dp 不管是推式子还是调试都不太拟人。
Code
#include<bits/stdc++.h>
#define ll long long
#define N 105
#define endl "\n"
#define fi first
#define se second
using namespace std;
ll mod=1e9+7;
const ll inf=1e18;
const double eps=1e-6;
namespace math_permutation{
ll fpow(ll x,ll y){
ll res=1;
while(y){
if(y&1)res=res*x%mod;
y>>=1,x=x*x%mod;
}
return res;
}
ll fac[N],ifac[N],inv[N];
void work(ll r){
fac[0]=inv[1]=1;
for(int i=1;i<=r;i++)fac[i]=fac[i-1]*i%mod;
ifac[r]=fpow(fac[r],mod-2);
for(int i=r;i>0;i--){
ifac[i-1]=ifac[i]*i%mod;
inv[i]=fac[i-1]*ifac[i]%mod;
}
}
ll C(ll n,ll m){
if(n<0||n<m)return 0;
return fac[n]*ifac[m]%mod*ifac[n-m]%mod;
}
void add(ll &x,ll y){
x%=mod,y%=mod;
x=(x+y+mod)%mod;
}
}using namespace math_permutation;
ll f[105][105],g[105][105];
ll n,m,k;
ll x1[N*N],x2[N*N],x3[N*N];
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>m>>k>>mod;
work(max(n,m));
f[0][0]=1;
x1[0]=x2[0]=x3[0]=1;
// ll st=clock();
for(int x=1;x<=k;x++){
for(int i=1;i<=n*m;i++){
x1[i]=x1[i-1]*(k-x+1)%mod;
x2[i]=x2[i-1]*(k-x)%mod;
x3[i]=x3[i-1]*x%mod;
}
for(int i=0;i<=n;i++)for(int j=0;j<=m;j++)g[i][j]=f[i][j],f[i][j]=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(g[i][j]==0)continue;
for(int d=0;d+i<=n;d++)
add(f[i+d][j],g[i][j]*C(n-i,d)%mod*x1[d*j]%mod*x3[d*(m-j)]%mod);
}
}
for(int i=0;i<=n;i++)for(int j=0;j<=m;j++)g[i][j]=f[i][j],f[i][j]=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(g[i][j]==0)continue;
for(int d=0;d+j<=m;d++)
add(f[i][j+d],g[i][j]*C(m-j,d)%mod*x1[d*i]%mod*x3[d*(n-i)]%mod);
}
}
for(int i=0;i<=n;i++)for(int j=0;j<=m;j++)g[i][j]=f[i][j],f[i][j]=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(g[i][j]==0)continue;
for(int d=0;d+i<=n;d++)
add(f[i+d][j],(d&1?-1ll:1ll)*g[i][j]*C(n-i,d)%mod*x2[d*j]%mod*x3[d*(m-j)]%mod);
}
}
for(int i=0;i<=n;i++)for(int j=0;j<=m;j++)g[i][j]=f[i][j],f[i][j]=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(g[i][j]==0)continue;
for(int d=0;d+j<=m;d++)
add(f[i][j+d],(d&1?-1ll:1ll)*g[i][j]*C(m-j,d)%mod*x2[d*i]%mod*x3[d*(n-i)]%mod);
}
}
//cout<<x<<" "<<(clock()-st)<<"ms"<<endl;
}
cout<<f[n][m];
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号