逃亡

### Description

　　数轴上有\(m\)个人，第\(i\)个人在\(x_i\)，每一时刻每个人会等概率往左边或者右边移动一单位长度，求\(n\)秒之后期望有多少个点被经过，答案对\(998244353\)取模

　　数据范围：反正就是\(n*m^2\)就好了（原来的那个范围给的太鬼畜了qwq）

　　

Solution

　　其实要求的就是每个点被经过的概率之和（因为每个点的贡献是\(1\)嘛）

　　直接求不好下手，考虑对于每一个人\(i\)求出：点\(x\)没有被经过的概率，记为\(P_i(x)\)

　　这样最后统计的时候就不用考虑那么多了，点\(x\)被经过的概率就是\(1-\prod\limits_{i=1}^m P_i(x)\)

　　现在每个人的影响就独立了，考虑对于一个人怎么求\(P_i(x)\)

​　　然后这个时候发现好像求\(x\)被经过的概率更加容易，所以我们转而求点\(x\)被第\(i\)个人经过的概率，\(P_i(x)\)的话直接用\(1\)减一下就出来了

　　按照\(n\)秒后这个人停下的位置\(ed\)分类，一个点\(x\)被经过有三种情况：\(ed<x\)，\(ed=x\)，\(ed>x\)

　　首先考虑\(x< ed\)的情况，记\(F(i)\)为这个人最后在\(i\)处停下的概率，那么这部分的结果为\(\sum\limits_{i=x+1}^{+\infty}F(i)\)（然而实际上当\(i\)与起点的距离大于\(n\)的时候\(F(i)=0\)，所以只用计算到起点\(+n\)的位置就好了）

　　然后看\(ed<x\)的情况，这部分看起来比较麻烦，因为我要走过\(x\)然后再折回来，这时候有一个很棒的处理方式：考虑以时间为\(x\)轴，位置为\(y\)轴建立坐标系，那么一种可行的方案画出来大概长这样：

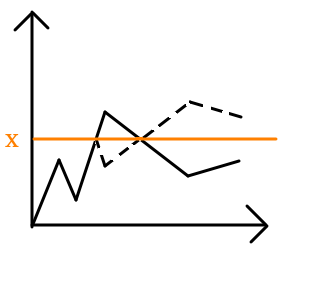
　　这个时候我们将第一次走到\(x\)的那个时刻之后的线段沿直线翻折上去，因为原来的终点\(ed\)是\(<x\)的，所以翻折之后新的终点一定是\(>x\)的，然后用这种方式我们就将一种\(ed<x\)的方案与唯一一种\(ed>x\)的方案对应上了，我们可以用计算\(x<ed\)的方式计算

　　再加上\(ed=x\)的情况，得到\(P_i(x)=1-(F(x)-2\sum\limits_{j=x+1}^{+\infty}F(j))\)

　　所以只要预处理出\(F\)的后缀和以及每个人可能到达的点的并集就好啦ovo

　　

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define pb push_back
using namespace std;
const int N=120000000,MOD=998244353,inf=2147483647;
struct seg{
	int l,r;
	seg(int _l=0,int _r=0){l=_l; r=_r;}
	bool merge(int l1,int r1){
		if (r1<l||r<l1) return 0;
		l=min(l,l1);
		r=max(r,r1);
		return 1;
	}
};
vector<seg> a;
int fac[N],invfac[N];
int sum[N];
int p[100010],st[100010];
int n,m,inv2;
int ans,L,R;
int mul(int x,int y){return 1LL*x*y%MOD;}
int plu(int x,int y){return (1LL*x+y)-(1LL*x+y>=MOD?MOD:0);}
int ksm(int x,int y){
	int ret=1,base=x;
	for (;y;y>>=1,base=mul(base,base))
		if (y&1) ret=mul(ret,base);
	return ret;
}
int C(int n,int m){return n<m?0:mul(fac[n],mul(invfac[m],invfac[n-m]));}
int F(int x){
	if ((x-n)&1) return 0;
	return mul(inv2,C(n,(n+x)/2));
}
void prework(int n){
	fac[0]=1;
	for (int i=1;i<=n;++i) fac[i]=mul(fac[i-1],i);
	invfac[n]=ksm(fac[n],MOD-2);
	for (int i=n-1;i>=0;--i) invfac[i]=mul(invfac[i+1],i+1);
	int tmp=ksm(2,MOD-2);
	inv2=ksm(ksm(2,n),MOD-2);
	sum[n+1]=0;
	for (int i=n;i>=1;--i) sum[i]=plu(sum[i+1],F(i));
}
int solve(int id){
	int tmp,x,p=1;
	int ret=0;
	for (int i=a[id].l;i<=a[id].r;++i){
		p=1;
		for (int j=1;j<=m;++j){
			x=abs(st[j]-i);
			if (x>n) continue;
			tmp=plu(1,MOD-plu(F(x),mul(2,sum[x+1])));
			p=mul(p,tmp);
		}
		ret=plu(ret,plu(1,MOD-p));
	}
	ret+=ret<0?MOD:0;
	return ret;
}

int main(){
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
#endif
	scanf("%d%d",&n,&m);
	for (int i=1;i<=m;++i) scanf("%d",st+i);
	sort(st+1,st+1+m);
	prework(n);
	int cnt=-1;
	for (int i=1;i<=m;++i){
		if (a.empty()) a.pb(seg(st[i]-n,st[i]+n)),++cnt;
		else{
			if (!a[cnt].merge(st[i]-n,st[i]+n))
				a.pb(seg(st[i]-n,st[i]+n)),++cnt;
		}
	}
	ans=0;
	for (int i=0;i<=cnt;++i)
		ans=plu(ans,solve(i));
	printf("%d\n",ans);
}