每天打卡一小时 第一天 编程四部曲

连续因子

一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：

输入在一行中给出一个正整数 N（1<N<231）。

输出格式：

首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。

 

编程四部曲

第一部曲 自然语言

 

运用双重循环，第一层循环从1到n的开方，第二层循环 计算乘积 ，在第二层循环里面判断是否符合 乘积 然后再比较序列的长短 是否记录

 

最后运用一层循环进行输出

 

第二部曲 流程图

 

 

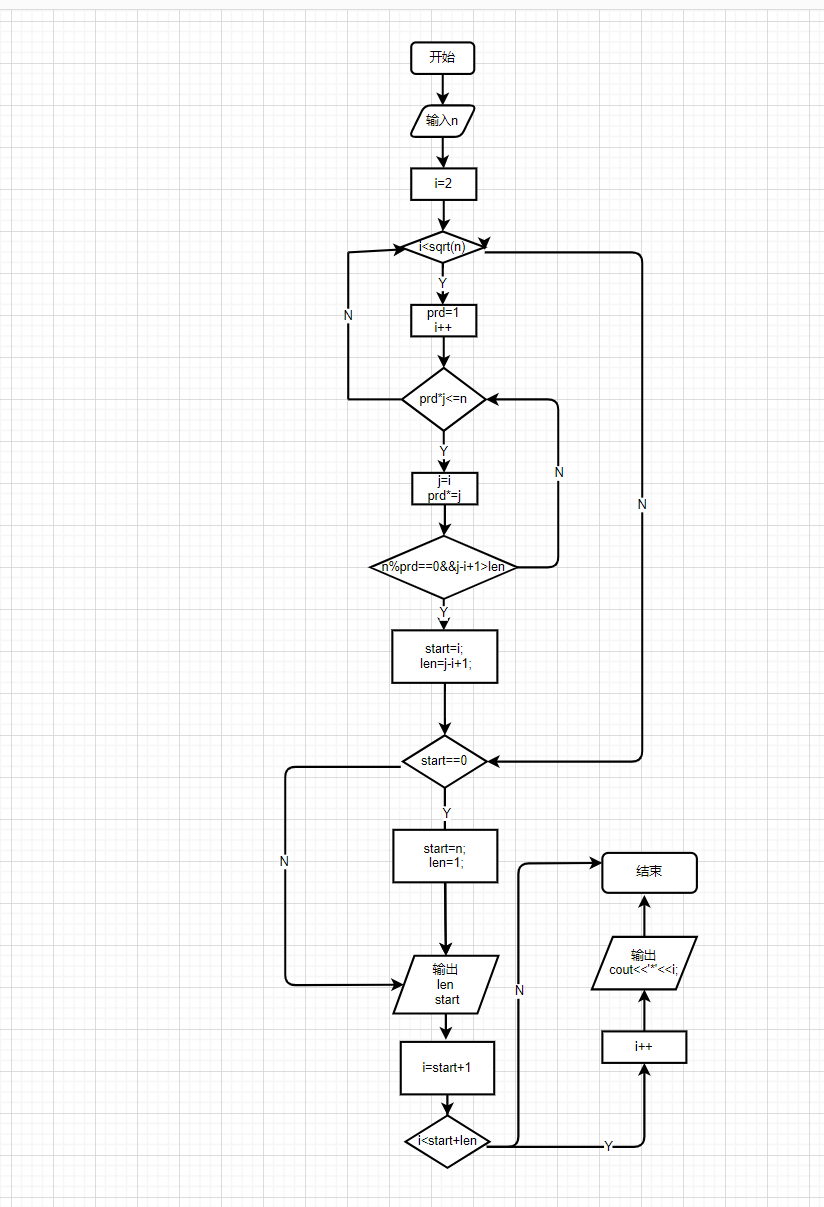
第三部曲 伪代码

C++头文件

 

主函数

{

  定义 长整性数据类型 n prd为零

  输入 n

  定义 整形数据类型 len  start均为零

  

 

For循环 条件i<=sqrt(n)   从i=2开始循环   i++

{

   Prd为1

   For循环 条件 ;prd*j<=n  定义 j等于i   j++

   {

 

    prd等于prd乘以j

     

   if判断  prd是否为n 的因子 合取 j减i加1 是否大于 len

{

   Start为i

   Len为 j减i加1

  

}

 

 

}

 

}

 

If 判断 start是否为零

start为n

        len为1

 

输出 len start

 

For循环 定义 i等于start加1   i小于start加上len i++

 

输出 *  i

}

 

源代码

 

#include <iostream>

#include <cmath>

using namespace std;

int main()

{

    long long n;

    cin>>n;

    

    int start=0,len=0;

    

    long long prd=0;

    

    for(int i=2;i<=sqrt(n);i++)

    {

        prd=1;

        

        for(int j=i;prd*j<=n;j++)

        {

            prd=prd*j;

            

            if(n%prd==0&&j-i+1>len)

            {

                start=i;

                len=j-i+1;

            }

            

        }

    }

    

    if(start==0)

    {

        start=n;

        len=1;

    }

    

        cout<<len<<endl<<start;

        for(int i=start+1;i<start+len;i++)

        {

            cout<<'*'<<i;

        }

}

 

第四部曲 总结

 

 

看似是暴力循环，其实是非常快速的解法

 

在优化代码的问题去考虑，不能只考虑是否正确，注重效率问题