BUAA_OO_第一单元总结

BUAA_OO_第一单元总结

　　第一单元主要目标是进行表达式解析。最终结果为完成能够提供自定义函数、求和函数、三角函数、幂函数及其嵌套的表达式解析程序。

第一次作业

作业要求

　　完成一个能够展开包含常数和幂函数的表达式的程序。其中常数为为带符号整数，幂函数为自变量为x，系数为0到8的可包含正号的整数。

类图分析

1.UML

• MainClass函数为程序入口，提供了表达式读入的功能。然后调用Expression，传入读入的表达式。
• Expression类在构造时就进行表达式解析，首先去除空格和多余的加减号，替换'**'以防解析错误。然后通过加减号分割，递归下降解析Term。将结果的Poly类相加或相减.
• Term类在构造时就完成解析，通过乘号分割，递归下降解析Factor。将结果的Poly类进行向乘。
• Factor类在构造时就完成解析。解析因子所带的正负号、类型（常数因子、变量因子、表达式因子）、指数。然后转化成Poly类进行储存。
• Poly类通过一个简单的数组进行储存。通过数组下标表示指数，数组内容储存系数。

代码度量

class	OCavg	OCmax	WMC
Expression	4.4	11.0	22.0
Factor	3.0	5.0	6.0
MainClass	1.0	1.0	1.0
Poly	3.125	10.0	25.0
Term	3.0	5.0	6.0
Total			60.0
Average	3.3333333333333335	6.4	12.0

类	总行数	代码行数	代码行数占比	注释行数	注释行数占比	空白行数	空白行数占比
Expression.java	82	75	0.9146341463414634	2	0.024390243902439025	5	0.06097560975609756
Factor.java	43	36	0.8372093023255814	4	0.09302325581395349	3	0.06976744186046512
MainClass.java	12	10	0.8333333333333334	0	0.0	2	0.16666666666666666
Poly.java	95	86	0.9052631578947369	0	0.0	9	0.09473684210526316
Term.java	28	24	0.8571428571428571	2	0.07142857142857142	2	0.07142857142857142

BUG分析

　　第一次作业在强测和互测中并没有出现bug。但是在性能上有部分缺陷。例如x**2到x*x的优化，表达式第一个项应该取符号为正的项的优化。

第二次作业

作业要求

　　第二次作业在第一次作业的基础上引入了三角函数、自定义函数和求和函数。仍然不要求多层嵌套括号的解析。三角函数包含sin和cos。求和函数自变量为i,上下限为正整数。自定义函数包含定义和调用。

类图分析

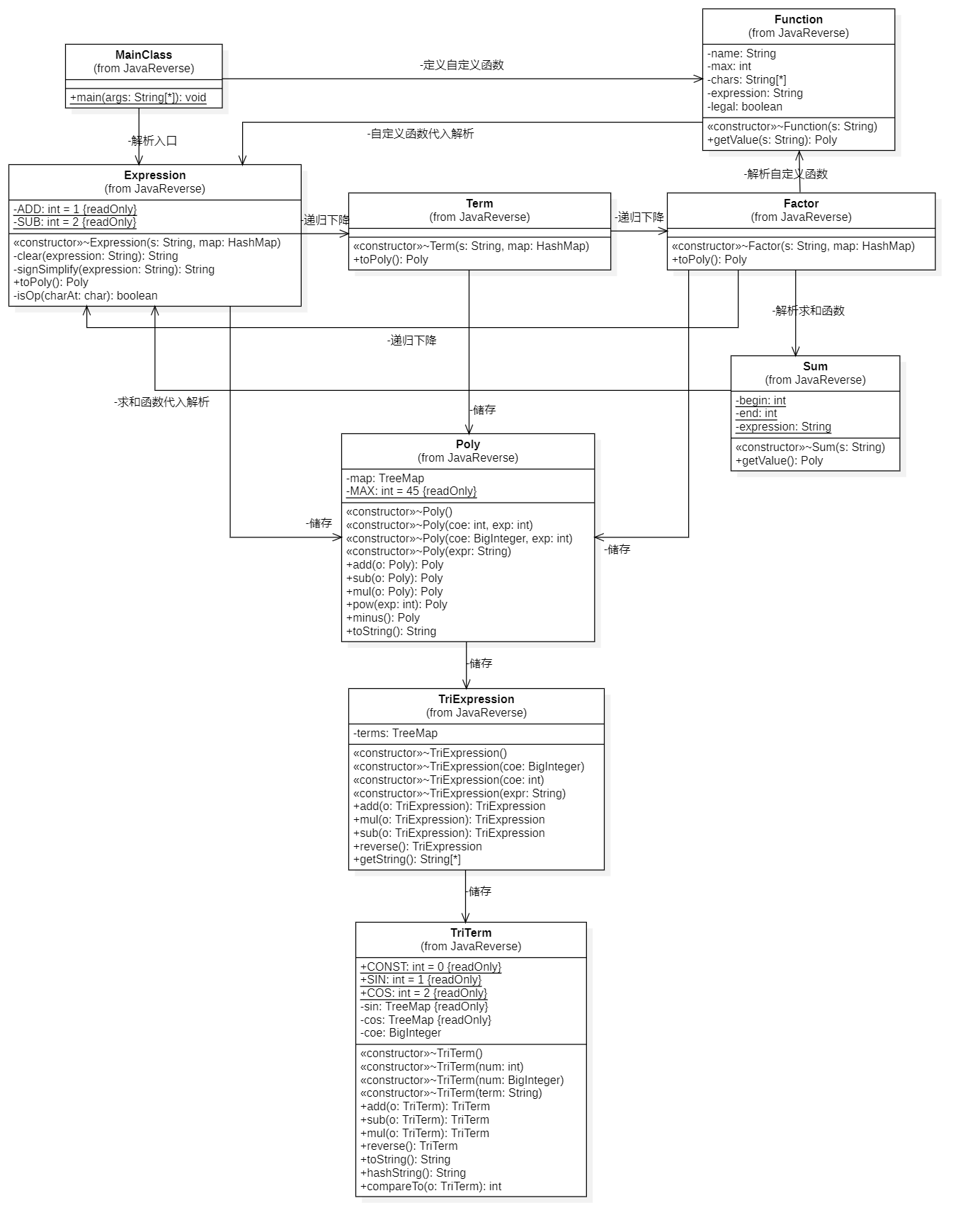
• MainClass为程序入口，首先进行了实例化Function类储存自定义函数。然后调用Expression类进行解析。
• Expression类、Term类在表达式处理方式与第一次作业相同。
• Factor类解析表达式时，除了第一次作业的解析方式外，增加了三角函数的解析。自定义函数调用、求和函数的解析分别调用Function类和Sum类进行解析。
• Function类搜索自变量，和调用的因子进行匹配，将定义的表达式中的自变量因子进行替换，然后调用Expression类进行解析。
• Sum类搜索自变量i，在求和表达式中将i替换为求和上下限范围中每一个整数，调用Expression类进行解析，然后将结果求和。
• Poly与第一次作业类似，但是由于三角函数的引入，储存的系数更改为TriExpression类。
• TriExpression类储存各个TriTerm。整个类储存了一个三角函数表达式，表示为\(\sum TriTerm\)。
• TriTerm类储存了一个常数和两个map，分别表示除三角函数外的系数和相乘的sin因子和cos因子。整个类储存了一个三角函数项，表示为\(const\prod sin(expression)\prod cos(expression)\)。

代码度量

class	OCavg	OCmax	WMC
Expression	4.4	11.0	22.0
Factor	4.5	8.0	9.0
Function	3.5	4.0	7.0
MainClass	2.0	2.0	2.0
Poly	2.6	8.0	26.0
Sum	3.0	4.0	6.0
Term	3.0	5.0	6.0
TriExpression	2.0	4.0	18.0
TriTerm	3.0	13.0	33.0
Total			129.0
Average	2.9318181818181817	6.555555555555555	14.333333333333334

类	总行数	代码行数	代码行数占比	注释行数	注释行数占比	空白行数	空白行数占比
Expression.java	84	76	0.9047619047619048	2	0.023809523809523808	6	0.07142857142857142
Factor.java	60	50	0.8333333333333334	7	0.11666666666666667	3	0.05
Function.java	46	43	0.9347826086956522	0	0.0	3	0.06521739130434782
MainClass.java	20	17	0.85	0	0.0	3	0.15
Poly.java	122	110	0.9016393442622951	1	0.00819672131147541	11	0.09016393442622951
Sum.java	37	34	0.918918918918919	0	0.0	3	0.08108108108108109
Term.java	30	25	0.8333333333333334	2	0.06666666666666667	3	0.1
TriExpression.java	88	77	0.875	0	0.0	11	0.125
TriTerm.java	183	166	0.907103825136612	5	0.0273224043715847	12	0.06557377049180328

BUG分析

　　第二次由于考虑不周在强测和互测中都被hack了。bug出现在sum函数的解析上。我采用了正则表达式解析sum的方式。上下限为带符号整数，在正则匹配时却没有匹配正号，因而导致了bug的产生。

第三次作业

作业要求

　　第三次作业要求支持括号的嵌套。其中包括表达式因子、三角函数因子、自定义函数调用内嵌套多层的括号。同时拓展了sum的上下限范围限制。

类图分析

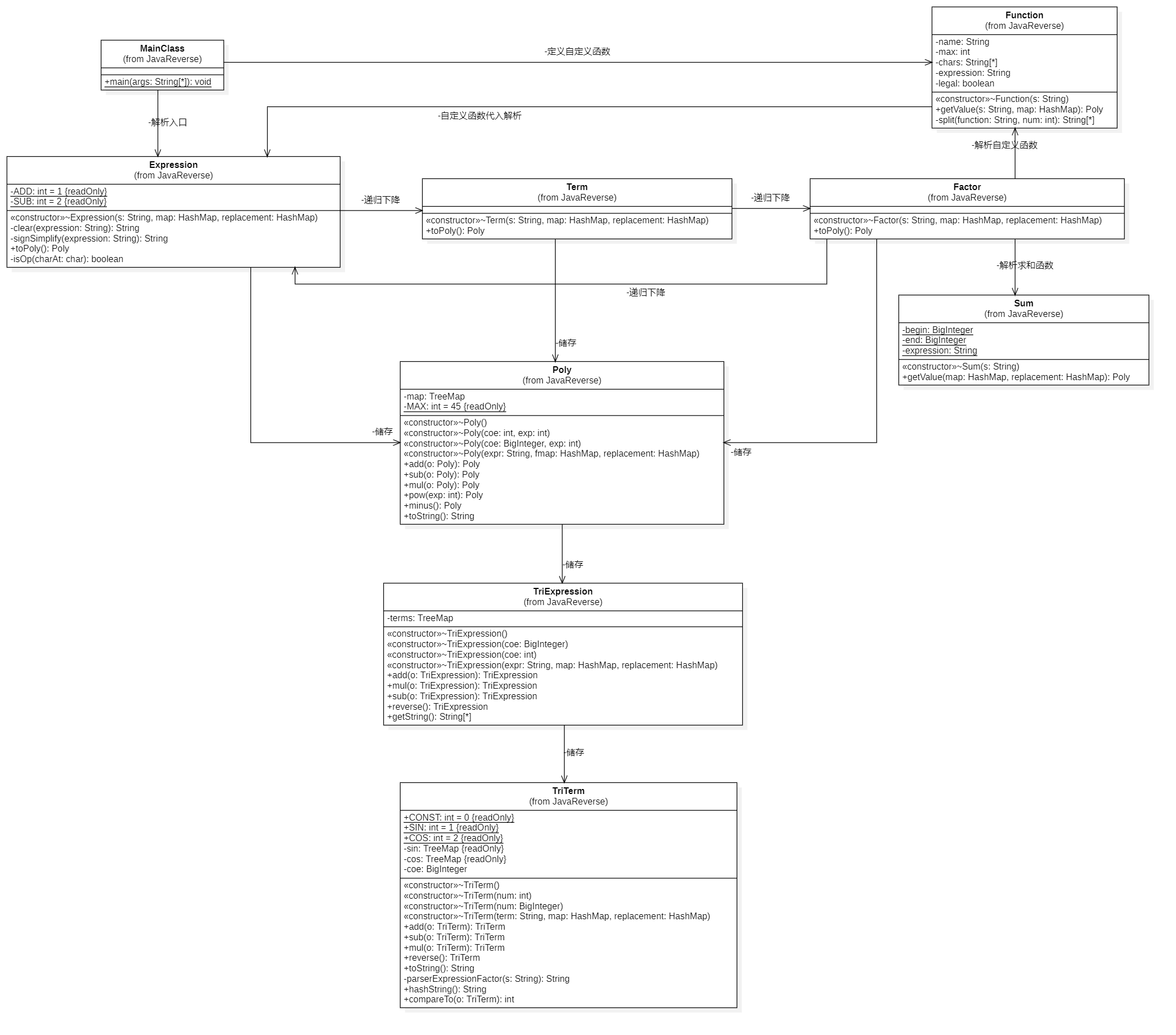
• 第三次作业架构与第二次作业基本相同，只是在部分类中做了修改。
• 首先是在Function和Sum类中，针对了自变量做了HashMap。该Map储存了自变量名称和调用时该自变量所代入的值。
• Factor类中增加了匹配上述自变量Map并替换其值的功能。
• 在TriTerm类中增加了toString时需要对表达式因子两侧增加括号的功能。

代码度量

class	OCavg	OCmax	WMC
Expression	4.4	11.0	22.0
Factor	7.0	13.0	14.0
Function	4.0	6.0	12.0
MainClass	2.0	2.0	2.0
Poly	2.6	8.0	26.0
Sum	2.5	3.0	5.0
Term	3.0	5.0	6.0
TriExpression	2.0	4.0	18.0
TriTerm	3.25	13.0	39.0
Total			144.0
Average	3.130434782608696	7.222222222222222	16.0

类	总行数	代码行数	代码行数占比	注释行数	注释行数占比	空白行数	空白行数占比
Expression.java	84	76	0.9047619047619048	2	0.023809523809523808	6	0.07142857142857142
Factor.java	80	66	0.825	11	0.1375	3	0.0375
Function.java	64	60	0.9375	0	0.0	4	0.0625
MainClass.java	20	18	0.9	0	0.0	2	0.1
Poly.java	123	111	0.9024390243902439	1	0.008130081300813009	11	0.08943089430894309
Sum.java	33	30	0.9090909090909091	0	0.0	3	0.09090909090909091
Term.java	30	25	0.8333333333333334	2	0.06666666666666667	3	0.1
TriExpression.java	90	79	0.8777777777777778	0	0.0	11	0.12222222222222222
TriTerm.java	205	186	0.9073170731707317	5	0.024390243902439025	14	0.06829268292682927
Total:	729	651	0.8930041152263375	21	0.02880658436213992	57	0.07818930041152264

BUG分析

　　第三次作业在强测和互测收到Hack比较严重，主要问题出在两个方面。
　　第一个方面是Sum函数中的上下限出现了bug，一是没有考虑负整数的情况，二是没有考虑到上下限为极大数的情况。还有就是Sum函数上限大于下限的情况,但是这个bug并没有遭到hack。
　　第二个方面是优化问题。在三角函数中，如果存在x+1,x**2+1等情况需要在两侧加括号。但是由于设计问题，我在输出时只考虑了序号大于0时的加、减、乘号，因而遇到了-x等情况就没有在两侧加上括号，而出了bug。

单元总结

架构设计

　　总体采用了递归下降的方式，从表达式到项再到因子，然后存在嵌套继续调用表达式解析。该递归下降的架构在后来进行迭代时，使代码有更好的扩展性。只需要增删部分方法就能够满足更多的功能。
　　从第一到第二次作业仅增加了自定义函数和求和函数的类，在因子解析时进行调用。然后将系数转换为三角函数表达式。第二次作业到第三次作业仅是完成了部分优化，代码在总体上几乎没有进行调整。

测评方式

　　我在第一次作业中依照作业的定义，对每部分的边界数据进行了汇总，然后排列组合手搓了小部分数据进行测试。于此同时，我也参考了GitHub上部分学长学姐的测评机，利用python进行了测评机的构建。
　　自动测评机主要包括两个部分，第一部分是数据生成器。首先通过random类进行选择生成哪种类型的数据，然后利用xger函数进行各种部分的数据生成。xger利用正则表达式生成相符合的字符串。将各种因子的正则表达提前进行定义就能够较快的生成数据。
　　第二部分是对拍程序。通过subprogress将生成的数据传入自己的程序，然后读出输出的数据。同时利用sympy库中的expand函数将生成的数据完全展开，并且展开程序输出的数据，比对两个结果的等价性。将程序的结果：超时、异常、结果不同等问题数据和输出结果写入保存结果的文件中，便于重现bug。
　　测评机在三次作业中都给予了我许多的帮助，在测试自己程序的正确性和互测中都起了较大的作用。利用该测评机，我在作业完成后都进行了较多的数据测试，因而除了由于审题问题和格式问题，测评机能够找出我程序的大部分bug，减少因程序不严谨而产生的问题。在互测中，我虽然进行了部分程序的阅读，但是由于程序的复杂性，都难以完全了解别人的程序。但是利用测评机，我在三次作业中都能够利用暴力测试发现许多同学的bug，发现了部分同学程序的错误或者较弱的拓展性。

感想总结

• 从架构的角度来看，一个好的架构对于程序的迭代开发具有极大的意义。在第一单元中，我都没有做过重构，但是仍能够较为清晰的完成程序。并且在第一第二次作业中完成了嵌套的功能，使得我在第三次的作业中几乎不需要进行调整。但是这也使得我花了较少的时间与精力在第三次作业的审题上，因而忽略了求和函数的限制变化。
• 从优化的角度来看，需要权量优化和正确性，进行取舍。第三次作业由于时间投入少，对于优化没有进行较好的处理，只是较为简单的判断了符号的存在，因而导致了部分情况没有考虑到位。因而需要权衡取舍程序的性能和正确性。同时在确定优化后，必须更加注意优化的正确性。在以后测评机中，可以考虑增加判断输出格式正确性的功能。
• 从代码的角度来看，我的代码在许多类中的操作复杂度仍很高，许许多多的方法都没有抽象出来，仍然还有面向过程的方式存在，在面对复杂对象是，没有办法很好的抽象、分割类和方法。