RNN反向传播？

\({\bf{h_t}}=f(\boldsymbol{Uh_{t-1}}+\boldsymbol{Wx_t}+\boldsymbol b)\),\({\bf{h}}为隐状态\)

\({\bf{y_t}}={\bf{Vh_t}}\)

同步的序列到序列模式 ,输入为一个长度为 𝑇 的序列 \({\bf{x_{1:T}}}=({\bf{x_1,...,x_T}})\),输出为序列 \(y_{1:T}=(y_1,...,y_T)\)

RNN反向传播计算时，\({\bf{U,W,b}}\)为参数

定义t时刻损失函数\(L_t=L(y_t,g({\bf{h_t}}))\)

整个序列的损失函数为\(L=\sum\limits_{t=1}^TL_t\)

整个序列的损失函数L关于参数\({\bf{U}}\)的梯度为\(\large\frac{\partial L}{{\partial \bf{U}}}=\sum\limits_{t=1}^T \frac{\partial L_t}{\partial {\bf{U}}}\),即每个时刻损失\(L_t\)关于参数\({\bf{U}}\)的偏导数之和

---

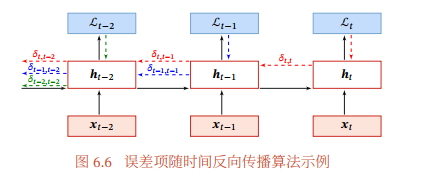
BPTT(随时间反向传播算法)

主要思想是通过类似前馈神经网络的错误反向传播算法[Werbos, 1990]来计算梯度

\({\bf{z_k}=Uh_{k-1}+Wx_k+b}\) \((1 \leq k \leq t)\)

假设\({\bf{x}}\)是m维的,\({\bf{z,h,b}}\)是n维的

\[{\bf{U}}=\begin{pmatrix} u_{11} & u_{12}&\cdots& u_{1n}\\ u_{21} & u_{22} &\cdots& u_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ u_{n1} & u_{n2} & \cdots &u_{nn} \end{pmatrix} $,${\bf{h_{k-1}}}=\begin{pmatrix} h_{k-1}^1\\ h_{k-1}^2 \\ \vdots \\ h_{k-1}^n \end{pmatrix}$,${\bf{z_{k}}}=\begin{pmatrix} z_{k}^1\\ z_{k}^2 \\ \vdots \\ z_{k}^n \end{pmatrix} \]

第t时刻损失函数\(L_t\)对参数\(u_{ij}\)的的梯度为 \(\large \frac{\partial L_t}{\partial u_{ij}}=\sum\limits_{k=1}^t \frac{\partial^+ {\bf{z_k}}}{\partial u_{ij}} \frac{\partial L_t}{\partial {\bf{z_k}}}\)

\(\large \frac{\partial^+ {\bf{z_k}}}{\partial u_{ij}}\)表示"直接"偏导数(保持\({\bf{h_{k-1}}}\)不变，对\(u_{ij}\)求导)

\(\large \frac{\partial^+ {\bf{z_k}}}{\partial u_{ij}}=[0,...[{\bf{h_{k-1}}}]_j,...,0]={\bf{I_i}}([{\bf{h_{k-1}}}]_j)\),例如对\(u_{11}\)求导为\(\begin{pmatrix} h_{k-1}^1\\ 0 \\ \vdots \\ 0 \end{pmatrix}\)

\([{\bf{h_{k-1}}}]_j\)为k-1时刻隐状态的第j维,\({\bf{I}}_i(x)\)表示除了第i行值为x外，其余都为0的行向量

定义误差项\(\large \delta_{t,k}=\frac{\partial L_t}{\partial {\bf{z_k}}}\)为第t时刻的损失对第k时刻隐藏神经层的净输入\({\bf{z_k}}\)的导数

\(\large {\bf{\delta_{t,k}}}=\frac{\partial L_t}{\partial {\bf{z_k}}}=\frac{\partial {\bf{h_k}}}{\partial {\bf{z_k}}}\frac{\partial {\bf{z_{k+1}}}}{\partial {\bf{h_k}}} \frac{\partial L_t}{\partial {\bf{z_{k+1}}}} =diag(f'({\bf{z_k}})){\bf{U}}^T{\bf{\delta_{t,k+1}}}\) \(1 \leq k < t\)

\(\large \frac{\partial {\bf{h_k}}}{\partial {\bf{z_k}}}= \begin{pmatrix} \frac{\partial h_k^1}{\partial z_1} & \frac{\partial h_k^1}{\partial z_2}& \cdots& \frac{\partial h_k^1}{\partial z_n} \\ \frac{\partial h_k^2}{\partial z_1} & \frac{\partial h_k^2}{\partial z_2} & \cdots & \frac{\partial h_k^2}{\partial z_n}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial h_k^n}{\partial z_1} & \frac{\partial h_k^n}{\partial z_2}& \cdots & \frac{\partial h_k^n}{\partial z_n} \end{pmatrix}= \begin{pmatrix} f'(z_1) & 0 & \cdots & 0 \\ 0 & f'(z_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & f'(z_n) \end{pmatrix}=diag(f'({\bf{z_k}}))\)

\[diag(f'({\bf{z_k}})) {\bf{U}}^T= \begin{pmatrix} f'(z_1)u_{11}&f'(z_1)u_{21}& \cdots &f'(z_1)u_{n1} \\ f'(z_2)u_{12} & f'(z_2)u_{22}& \cdots & f'(z_2)u_{n2}\\ \vdots & \\ f'(z_n)u_{1n} & f'(z_n)u_{2n} & \cdots & f'(z_n)u_{nn} \end{pmatrix} $,$\large {\bf{\delta_{t,k}}}=\begin{pmatrix} \delta_{t,k}^1 \\ \delta_{t,k}^2 \\ \vdots \\ \delta_{t,k}^n \end{pmatrix} $,${\bf{I_i}}{\bf{\delta_{t,k}}}=[\delta_{t,k}]_i \]

\(\large \frac{\partial L_t}{\partial u_{ij}}=\sum\limits_{k=1}^t [{\bf{\delta_{t,k}}}]_i[{\bf{h_{k-1}}}]_j\)，写成矩阵形式为\(\large \frac{\partial L_t}{\partial {\bf{U}}}=\sum\limits_{k=1}^t {\bf{\delta _{t,k}}}{\bf{h^T_{k-1}}}\)

\(\large \frac{\partial L_t}{\partial {\bf{U}}}= \sum\limits_{k=1}^t \begin{pmatrix} \frac{\partial L_t}{\partial u_{11}} & \frac{\partial L_t}{\partial u_{12}} & \cdots & \frac{\partial L_t}{\partial u_{1n}} \\ \frac{\partial L_t}{\partial u_{21}} & \frac{\partial L_t}{\partial u_{22}} & \cdots & \frac{\partial L_t}{\partial u_{2n}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial L_t}{\partial u_{n1}} & \frac{\partial L_t}{\partial u_{n2}} & \cdots & \frac{\partial L_t}{\partial u_{nn}} \end{pmatrix}\)=\(\sum\limits_{k=1}^t \begin{pmatrix} \delta_{t,k}^1h_{k-1}^1 & \delta_{t,k}^1h_{k-1}^2 & \cdots & \delta_{t,k}^1h_{k-1}^n\\ \delta_{t,k}^2h_{k-1}^1 & \delta_{t,k}^2h_{k-1}^2 & \cdots & \delta_{t,k}^2h_{k-1}^n\\ \vdots & \vdots & \ddots & \vdots \\ \delta_{t,k}^nh_{k-1}^1 & \delta_{t,k}^nh_{k-1}^2 & \cdots & \delta_{t,k}^nh_{k-1}^n\end{pmatrix}\)

\(\large \frac{\partial L}{\partial {\bf{U}}}=\sum\limits_{t=1}^T \sum\limits_{k=1}^t {\bf{\delta _{t,k}}}{\bf{h^T_{k-1}}}\)

---

同理，关于\({\bf{W}}\)和\({\bf{b}}\)的梯度为

\(\large \frac{\partial L}{\partial {\bf{W}}}=\sum\limits_{t=1}^T \sum\limits_{k=1}^t {\bf{\delta _{t,k}}}{\bf{x^T_{k}}}\)

\(\large \frac{\partial L}{\partial {\bf{b}}}=\sum\limits_{t=1}^T \sum\limits_{k=1}^t {\bf{\delta _{t,k}}}\)

---

RTRL(实时循环学习算法 ）

通过前向传播的方式来计算梯度

第t+1时刻的状态\({\bf{h_{t+1}}}\) 为 \({\bf{h_{t+1}}}=f(z_{t+1})=f({\bf{Uh_t+Wx_{t+1}}+b})\)

关于\(u_{ij}\)的偏导数为

\(\large \frac{\partial \bf{h_{t+1}}}{\partial u_{ij}}=(\frac{\partial^+\bf{z_{t+1}}}{\partial u_{ij}}+\frac{\partial \bf{h_t}}{\partial u_{ij}} {\bf{U}^T} )\frac{\partial \bf{h_{t+1}}}{\partial z_{t+1}}=({\bf{I_i}}([{\bf{h_t}}]_j)+\frac{\partial{\bf{h_t}}}{\partial u_{ij}}{\bf{U}}^T)diag(f'({\bf{z_{t+1}}}))\)

从1时刻开始，同时计算\({\bf{h_t}}\)和\(\large \frac{\partial {\bf{h_1}}}{\partial u_{ij}},\frac{\partial {\bf{h_2}}}{\partial u_{ij}},\frac{\partial {\bf{h_3}}}{\partial u_{ij}}...\)

假设第t时刻的损失函数为\(L_t\),可以同时计算损失函数对\(u_{ij}\)的偏导数 \(\large \frac{\partial L_t}{\partial u_{ij}}=\frac{\partial {\bf{h_t}}}{\partial u_{ij}} \frac{\partial L_t}{\partial {\bf{h_t}}}\)

在t时刻就可以实时计算\(L_t\)对参数\({\bf{U}}\)的梯度，并更新梯度

梯度计算仍为\(\large\frac{\partial L}{{\partial \bf{U}}}=\sum\limits_{t=1}^T \frac{\partial L_t}{\partial {\bf{U}}}\)