如何理解EM算法？

如何理解EM算法？

在计算概率模型的时候，一般使用极大似然估计得到似然函数求解参数，如果存在隐藏变量，无法直接使用数据。这时候就考虑使用EM算法求解。

此时:\(\large {\bf{\theta}} = arg\max \limits_{\theta} \sum\limits_{i=1}^mlogP({\bf{x^i}};{\bf{\theta)}}\) 中的\({\bf{\theta}}\)是无法求解

分解上式\({\bf{\theta}}=\arg \max \limits_{\bf{\theta}}\sum\limits_{i=1}^m log \sum \limits_{z^i} P({\bf{x^i}},z^i,\bf{{\theta}})\)，隐藏变量为z

上式中\(\sum\limits_{z^i}\)的意思是对样本\(i\)的每个可能类别求和

---

如果引入概率分布\(Q_i(z_i)\)，每个样本都有一个\(Q_i(z_i)\)，即\(\sum \limits_{z^i}Q_i(z_i)=1,Q_i(z_i) \geq 0\)，则利用这种分布可以对似然函数分解

\(\begin{aligned} \sum_{i=1}^{m} \log \sum_{z^{(i)}} P\left(x^{(i)}, z^{(i)} ; \theta\right) &=\sum_{i=1}^{m} \log \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} \\ & \geq \sum_{i=1}^{m} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} \end{aligned}\)

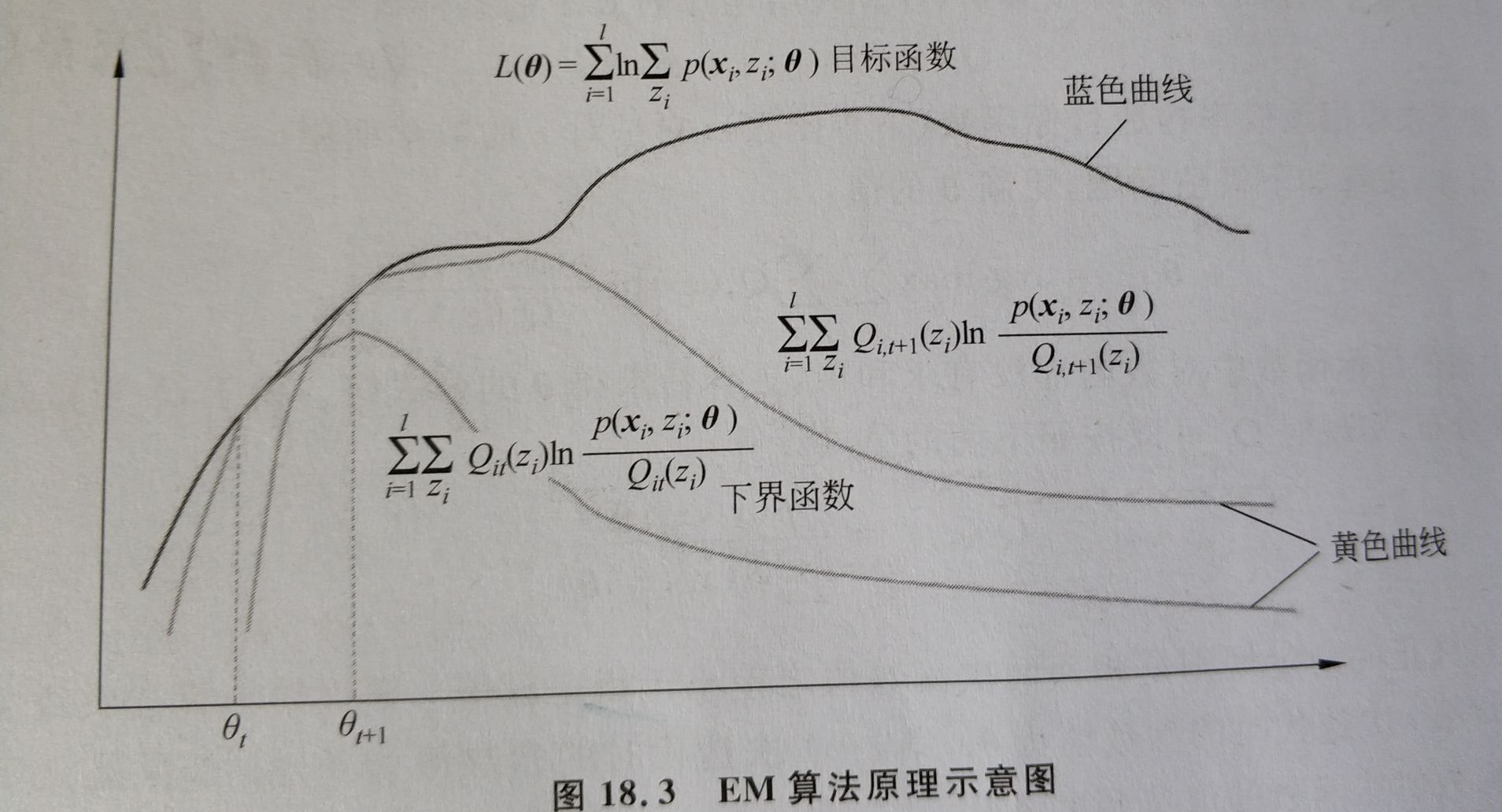
上式构造出一个下界函数，提升下界函数的值，能使对数似然函数的值也提高。从而优化目标变为：

\(\large \arg \max \limits_{\theta} \sum\limits_{i=1}^{m} \sum_{z^{(i)}} Q_{i}\left(z^{(i)}\right) \log \frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)}\)

在Jensen不等式中，当取值为常数时，等号成立，则当$\large \frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q_{i}\left(z^{(i)}\right)} = c $ 时，下界函数=对数似然函数，

由\(\large \sum\limits_{z^i}P({\bf{x^i}},z^i;{\bf{\theta}})=\sum\limits_{z^i}Q_i(z^i)c\)

可以推出\(\large \sum\limits_{z^i}P({\bf{x^i}},z^i;{\bf{\theta}})=c\)，\(\large Q_{i}\left(z^{(i)}\right)=\frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{\sum\limits_{z^i} P\left(x^{(i)}, z^{(i)} ; \theta\right)}=\frac{P\left(x^{(i)}, z^{(i)} ; \theta\right)}{P\left(x^{(i)} ; \theta\right)}=P\left(z^{(i)} | x^{(i)} ; \theta\right)\)

\(\bf{\theta}\)给定，令\(Q_i(Z^i)=P(z^i|{\bf{x^i;\theta}})\)，此时下界函数=对数似然函数。

更新\(\bf{\theta}\)，极大化下界函数的值，此时对数似然函数也在变大。

再以更新后的\(\bf{\theta}\)计算\(Q_i(z^i)\)，如此迭代更新\(\bf{\theta}\)，对数似然函数也不断变大

E步：

​ 构造下界函数，当\(Q_i(z^i)\)=\(z^i\)的条件概率时，下界函数是基于条件概率的期望，此时下界函数值=对数似然函数值

M步：

​ 极大化下界函数，更新\(\theta\)，此时对数似然函数也变大