对极值点偏移的思考 （还在咕咕咕，别急

待解决

对极值点偏移的思考
杭州二中 小 Z

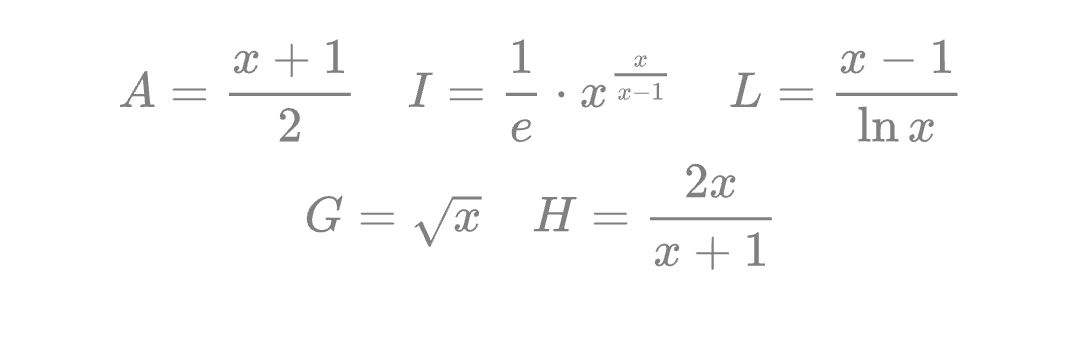
我常常在思考着：与其题海战术，不如回归最原始的题目，去挖掘它更深层次的性质，单单研究一题足矣。

因此，本文我只对刚入门时学的函数 \(f(x)=\frac{\ln x}{x}=a\ (a\in (0,\frac 1e])\) 进行讨论。

可能有人会问：\(f(x)=x-\ln x=b\ (b\in [1,+\infty))\) 也是入门时学的，为啥不讨论它呢？原因很简单：他俩本质相同。

\[\begin{aligned} &&x-\ln x&=b \\ &\iff&\ln \frac{e^x}{x} &=b \\ &\iff& \frac{e^x}{x} &= e^b \\ &\iff& \frac{\ln e^x}{e^x}&=e^{-b} \end{aligned} \]

可见它就是前者所有值 \(\ln\) 以后（值域再取反）的结果，由此也说明了它们值域之间的关系并非巧合。

常见的极值点偏移题目，会考 \(x_1+x_2\)，\(|x_1-x_2|\)，\(x_1\cdot x_2\) 与关于极值点 \(x_0\) 或值 \(a\) 的函数间的大小关系，因此我们就这些展开讨论。

我重在叙述思考过程，最终的书写我认为是次要的。

保证每一问内部的界越来越紧，且在市面上的教辅中找不着（几乎都是导数爱好者原创的）。做法也并非原创，但是一定是融入了自己的理解与思考的。

本文将会介绍的一些思考角度：

  • 主元与拟合；
  • 同构；
  • 泰勒展开；
  • 函数凹凸性；
  • 帕德逼近；
  • 拉格朗日反演；
  • 拉格朗日中值定理；

已知函数 \(f(x)=\frac{\ln x}{x}\)，设 \(x_1,x_2\ (x_1\neq x_2)\) 满足 \(f(x_1)=f(x_2)=a\ (a\in (0,\frac 1e])\)，求证：
第 1 问·热身. \(x_1+x_2>2e\)
第 1 问·小试牛刀. \(x_1+x_2>\frac{2}{a}\)
第 1 问·挑战. \(x_1+x_2>\frac{1-\ln a}{a}\)
第 1 问·登峰造极. \(x_1+x_2>\frac{10}{3a}-\frac{4e}{3}\)
注：第 1 问·登峰造极是我所知的最紧的界。

解答

第 1 问·热身 & 小试牛刀

观察到 \(\frac{\ln x}{x}\) 的形式可以凑成对数不等式，所以 \(\frac{x_1+x_2}{2}> \frac{x_1-x_2}{\ln x_1-\ln x_2}=\frac{1}{a}\)，因此 \(x_1+x_2> \frac{2}{a}>2e\)。

第 1 问·挑战

处理超越函数不方便，所以我们尝试构造一个“朴素”的函数，满足极值点不变，左右两侧和原函数的大小相反。

不难发现 \(g(x)=\frac{3x-e}{x(x+e)}\) 就满足条件，它在 \(x\in (0,e)\) 处 \(g(x)>f(x)\)，\(x\in (e,+\infty)\) 处 \(g(x)<f(x)\)。

因此，它和 \(y=a\) 交出的两点 \(x_3,x_4\) 满足 \(x_3<x_1<e<x_4<x_2\)。

将 \(g(x)\) 移项为一个二次函数可得 \(x_3\cdot x_4=\frac{e}{a}\)，因此

\[\begin{aligned} &&x_1\cdot x_2&>x_3\cdot x_4=\frac{e}{a} \\ &\Rightarrow&\ln x_1+\ln x_2&> 1-\ln a \\ &\Rightarrow&x_1+x_2&>\frac{1-\ln a}{a} \end{aligned} \]

第 1 问·登峰造极

前置知识：

  • 不等式链：几何平均 \(G(a,b)\le\) 对数平均 \(L(a,b)\le\) 指数平均 \(I(a,b)\le\) 算术平均 \(A(a,b)\)。

\[\sqrt{ab}\le \frac{b-a}{\ln b-\ln a}\le \frac{1}{e}\left(\frac{b^b}{a^a}\right)^{\frac{1}{b-a}}\le \frac{a+b}{2} \]

第 2 问·热身. \(x_1+x_2<\frac{-2\ln a}{a}\)
第 2 问·挑战. \(x_1+x_2<\frac{2-4\ln a}{3a}\)
注：第 2 问·挑战是该形式下最紧的界。

解答

第 2 问·热身

同样用对数不等式，\(\frac{x_1-x_2}{\ln x_1-\ln x_2}\ge \sqrt{x_1\cdot x_2}\)，采用类似第 1 问·挑战 1后半段的套路即可。

\[\begin{aligned} &&x_1\cdot x_2&<\frac{1}{a^2}\\ &\Rightarrow&\ln x_1+\ln x_2&< -2\ln a \\ &\Rightarrow&x_1+x_2&<\frac{-2\ln a}{a} \end{aligned} \]

第 3 问·热身. \(|x_1-x_2|>\sqrt{1-ae}\)
第 3 问·小试牛刀. \(|x_1-x_2|>\frac{\sqrt{1-ae}}{a}\)
第 3 问·更近一步. \(|x_1-x_2|>\frac{2\sqrt{1-ae}}{a}\)
第 3 问·挑战. \(|x_1-x_2|>\sqrt{8e\left(\frac 1a-e\right)}\)
第 3 问.登峰造极. \(|x_1-x_2|>2\sqrt{\left(\frac 1a-e\right)\left(\frac 3a-e\right)}\)
第 3 问·不愧是你. \(|x_1-x_2|>\frac 23 \sqrt{\left(\frac 1a-e\right)\left(\frac {29}{a}-11e\right)}\)
注：第 3 问·不愧是你是该形式下最紧的界，系数是最佳的。

解答

第 4 问. 显然 \(|x_1-x_2|\) 可以趋于无穷大，所以没必要讨论它。

第 5 问·热身. \(x_1\cdot x_2>e^2\)
第 5 问·挑战. \(x_1\cdot x_2>\frac{e}{a}\)

解答

第 5 问·热身 & 挑战

考虑

\[\begin{aligned} &&\frac{x_1+x_2}{\ln x_1+\ln x_2}&=\frac{1}{a} \\ &\Rightarrow& \ln x_1+\ln x_2&=a(x1+x2) \\ &\Rightarrow& x_1\cdot x_2&=e^{a(x_1+x_2)} \end{aligned} \]

代入第 1 问·挑战的结论，可得 \(x_1\cdot x_2>\frac{e}{a}>e^2\)。

第 6 问·热身. \(x_1\cdot x_2<\frac{1}{a^2}\)
第 6 问·挑战. \(x_1\cdot x_2<e^{\frac 23}\cdot a^{-\frac 43}\)

解答

第 6 问·热身 & 挑战

代入第 2 问的结论即可。

参考资料

posted @ 2022-08-14 15:01  wlzhouzhuan  阅读(652)  评论(0)  编辑  收藏  举报