学习数学刷教科书上的题有没有用?| 知乎问答
前情概要
在知乎上看到这个问题,学习数学刷教科书上的题有没有用? - 知乎,结合自己的教学实践和学生的学习实际,我也来谈谈自己的浅显看法,也欢迎各位交流。
理论说教
高中学生,尤其是高三学生,基本非常迷信现在市面上流行的各种复习资料,高三一年的复习,基本上就是脱离教材来学习数学,好多一线的老师都不大赞成这个做法,认为学生舍本逐末,我也赞成这个看法。这种不好的学习趋势,导致高一和高二的学生在初次学习新内容时,往往看不起教科书上配备的例题和习题,总想着那些大而全的资料是宝典,他们的想法一般都是想着怎么能一步到位,将数学知识一次挖掘清楚,结果大多学生的学习效果不如意,平时的自我感觉良好,一到考试就傻眼了,我们可以从以下的角度来试着分析:
数学知识的掌握,尤其体现我们的认知是螺旋上升的特质,往往不会一步到位,缺少一环,数学概念的理解、掌握和应用都会成问题。
编写了近乎9年多的博客,也基本能体会教科书在编写时需要考虑的问题了。一个数学概念的引入,到建立印象,到学生理解,再到学生掌握,最后到学生会被动应用和主动应用,编写者需要考虑的问题很多很多,而教科书受各种因素的限制,不可能编写的很厚,好多地方只能一笔带过,比如,教科书上会说,显而易见,同理 这样的话语,但是对于不同的个体而言,有的学生要理解同理,要理解显而易见,可能需要3-4页的配备内容,你要是经常阅读我的博客,你会有比较深刻的印象,因为我往往在这些地方会做出自己的数学解释,而且还带有特殊的显示方式,也不影响阅读体验,所以你会觉得我做的好,主要是我的解释不受篇幅的限制,对于理解这个知识点能用到的所有的要素我基本都能配备齐全,比如,文字,图片,音频,视频,课件,动态课件,立体课件等等,这些内容于教材是做不到的。
那么,编写者在选编内容时必然会思之又思,慎之又慎,你得用有限的篇幅来展现尽可能多的想法和内容,所以一本教材会配备有一本教科书的使用说明,我们叫教师教学用书,这些都是国家层面的,基本不会糊弄。一般来说,例题都是精挑细选的,课后练习的配备也是一样的,以课后习题为例,有当堂练习题,这个是初次接触了数学概念后的简单层次上的小试牛刀,比较简单,思维层次比较低,然后一个单元后边会配备分层次的习题,常见 \(A\)、\(B\)、\(C\) 三个层次,高一高二的学生作业往往会从这些组里面选,难度是递进的,有些也是留给学有余力的学生学习的。这是所学知识在消化了大概一周之内的用题,等到一个单元,也就是一个月左右,还有个章末习题,也是分组的,这个难度又有所增加,这是第三个层次。到这个时候,所学的数学知识点大概能理解和掌握个70%-80%,当然还需要高三的提炼。如果你把这些东西,真正的挖掘到位了,你就不会再问自己,刷教科书上的题目到底有没有用。
再者,这个编写质量和市面上的东西相比,质量如何呢,你可以这样想,教材的使用范围,使用人群即受众是最广的,那些网红的资料是比不了的,而且教材的编写会后质量保证,你编写错了,那还了得,弄错了,你不得被人讨伐呀,网红资料错了也就错了,谁会追究责任,这样一想,许多问题就不成问题了,你也就容易接受教科书了,现在网上好多人说教材是反自学的,主要与教材篇幅、价格、市场等有很大关系,怪不了编写者,编写者的站位往往比较高,不是一般人能比得了的,基本都是行业和专业领域的翘楚。
在这个纷繁复杂的世界里,学会分析,学会思考,学会选择,非常的重要。
以上是我们使用教科书时,能想到的,除此之外,当然还需要老师的适当调整,适时的增删,自习辅导,晚自习辅导等的配合,及时答疑解惑,才可能再提升。说到这里,想到电视剧《大染坊》里的陈六子,一个叫花子,社会的最底层,没钱读书,从说书先生口中听到一句话,一等人,不用教;二等人,用言教;三等人,用棍教;首先申明,这个话不对,但道理是放之四海而皆准的。懂得都懂,你自己琢磨吧。
那么新问题来了,我们该如何用教科书?怎么样用才是高效的?
典型案例
- 我们以圆锥曲线中的椭圆的第二定义和第三定义为例来作典例印证,说明如何使用教材和整理笔记。
圆锥曲线的由来动画演示:
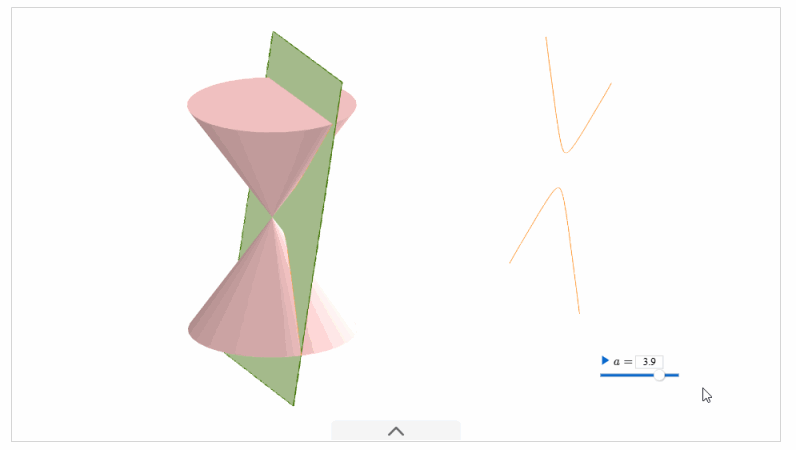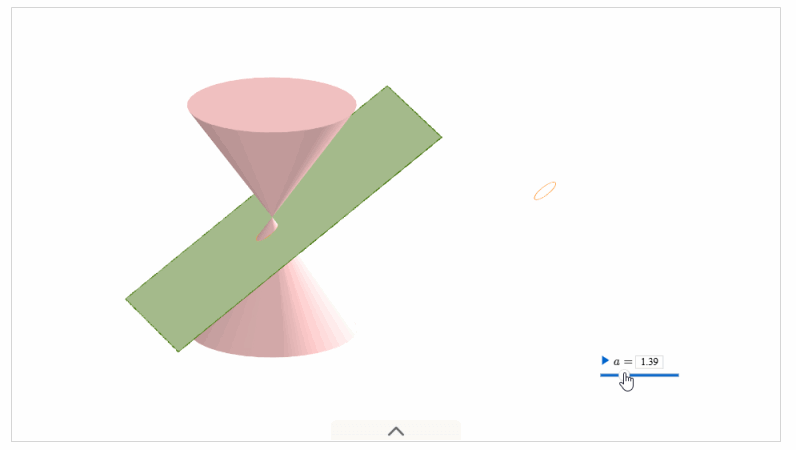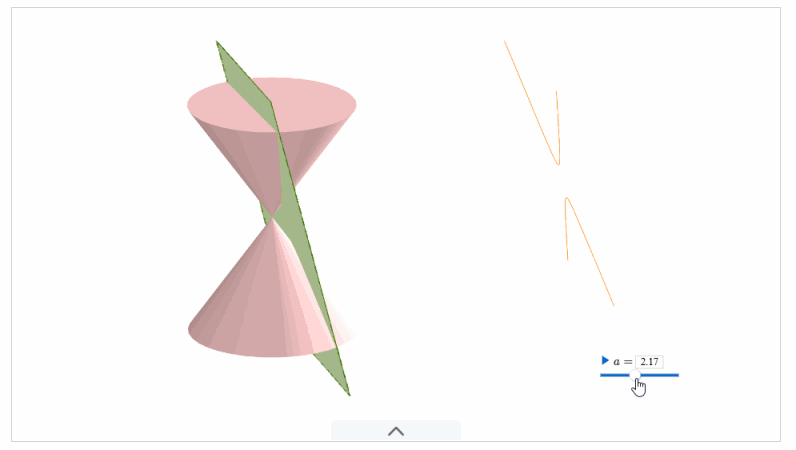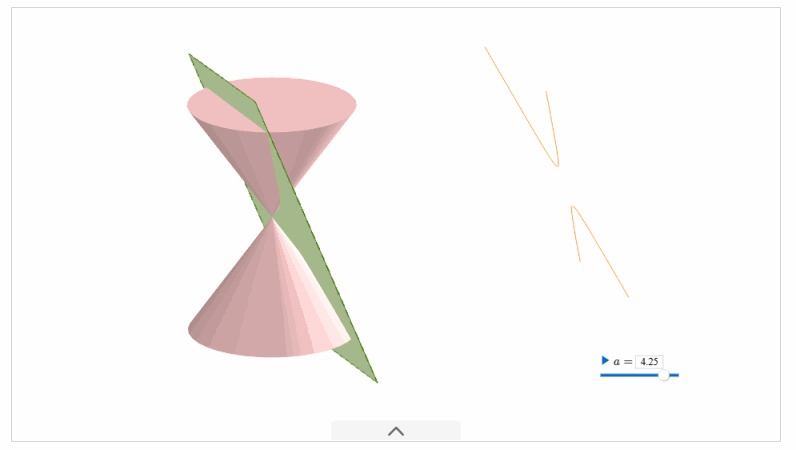
在新版人教 \(2019 A\) 版教材中,我们分别学习了三种圆锥曲线的定义,她们都属于各自的第一定义,也是学生最好理解和接受的定义。椭圆的定义,双曲线的定义,抛物线的定义
第二定义的演变
大概在2006年左右,圆锥曲线的第二定义[或称为统一定义]是明确要学习的,到2012年左右学生反应数学难,因此又不要求学习了,到新版人教 \(2019 A\) 版教材中虽然没有明确提出要学习第二定义,但是教材中满是第二定义的影子,不信,我们看看教材的编排:
先说结论:圆锥曲线的统一定义:平面上一动点 \(M(x,y)\) 到一个定点 \(F(c,0)\)(或 \(F'(-c,0)\) ) 的距离和它到定直线 \(l:x=\cfrac{a^2}{c}\)(或 \(l':x=-\cfrac{a^2}{c}\)) 的距离之比为常数 \(\cfrac{c}{a}\) ,若 \(0<\cfrac{c}{a}<1\) 时,轨迹是椭圆;若 \(\cfrac{c}{a}=1\) 时,轨迹是抛物线;若 \(\cfrac{c}{a}>1\) 时,轨迹是双曲线。
椭圆第二定义探究
- 数字案例
说明:这是椭圆第二定义的具体数字案例1,没有做抽象概括,让学生初次体会,满足这个条件的曲线是椭圆。本案例中 \(0<\cfrac{c}{a}=\cfrac{4}{5}<1\); 教材上例题的详细求解过程
- 对应练习
说明:这是上述例题的强化,椭圆第二定义的具体数字案例2,椭圆标准方程的再认识,本练习中 \(0<\cfrac{c}{a}=\cfrac{1}{2}<1\); 可以仿上自行完成求解,结论:
- 抽象概括
✍️已知动点 \(M(x,y)\) 与定点 \(F(c,0)\) 的距离和 \(M\) 到定直线 \(l:\)\(x\)\(=\)\(\cfrac{a^2}{c}\) 的距离之比为常数 \(\cfrac{c}{a}\),且 \(0\)\(<\)\(\cfrac{c}{a}\)\(<\)\(1\);试证明动点 \(M\) 的轨迹是椭圆 .
证明:由于动点 \(M(x,y)\) 与定点 \(F(c,0)\) 的距离为 \(|MF|\) \(=\) \(\sqrt{(x-c)^2+(y-0)^2}\),动点 \(M(x,y)\) 到定直线 \(l:\)\(x\) \(=\)\(\cfrac{a^2}{c}\) 的距离为 \(d\) \(=\) \(|x-\cfrac{a^2}{c}|\),
由题目可知,\(\cfrac{|MF|}{d}\) \(=\) \(\cfrac{c}{a}\),即 \(\cfrac{\sqrt{(x-c)^2+(y-0)^2}}{|x-\cfrac{a^2}{c}|}\) \(=\) \(\cfrac{c}{a}\),
两边同时平方,得到 \(\cfrac{(x-c)^2+y^2}{(x-\cfrac{a^2}{c})^2}\) \(=\) \(\cfrac{c^2}{a^2}\),
变形整理为,\((a^2-c^2)\)\(\cdot\)\(x^2\)\(+\)\(a^2\)\(\cdot\)\(y^2\)\(=\)\(a^2\)\(\cdot\)\((a^2-c^2)\),
由于 \(0<\cfrac{c}{a}<1\),则 \(a^2-c^2>0\),为美观标准,我们令 \(a^2-c^2=b^2\) \((b>0)\),代入上式整理为,
\(b^2x^2+a^2y^2=a^2b^2\),两边同时除以 \(a^2b^2\)得到,椭圆的标准方程为
故动点 \(M\) 的轨迹是椭圆,上式表明它是焦点在 \(x\) 轴上的椭圆,其中定点 \(F(c,0)\) 即右焦点,定直线 \(l:\)\(x\)\(=\)\(\cfrac{a^2}{c}\) 为与定点 \(F\) 相对应的右准线 . 由此若要继续研究,我们自然能得到左焦点和左准线 .
- 对应教材上的探究安排
椭圆的第三定义引入
在人教 \(2019A\) 版选择性必修一 \(P_{121}\) \(3.2.1\) 的探究内容中,其实已经涉及到双曲线的第三定义【类比此例,我们可以得到椭圆的第三定义】,在下面的例子中一并解答;

典例剖析
解:设点 \(M(x,y)\),则由 \(k_{MA}=\cfrac{y-0}{x+5}\), \(k_{MB}=\cfrac{y-0}{x-5}\), \(k_{MA}\cdot k_{MB}=-\cfrac{16}{25}\),
可得到,\(\cfrac{y-0}{x+5}\times\cfrac{y-0}{x-5}=-\cfrac{16}{25}\),
整理得到 \(\cfrac{x^2}{25}+\cfrac{y^2}{16}=1\),但是 \(x\neq\pm 5\),如下图所示
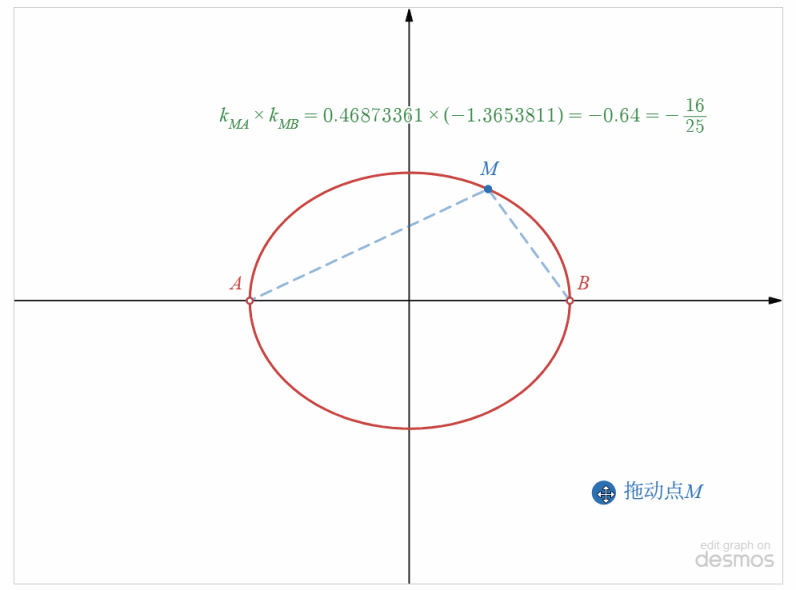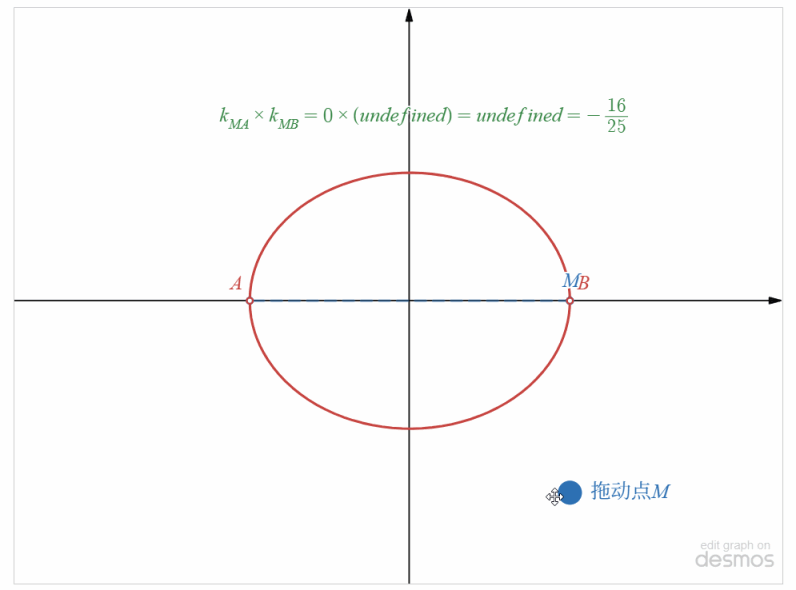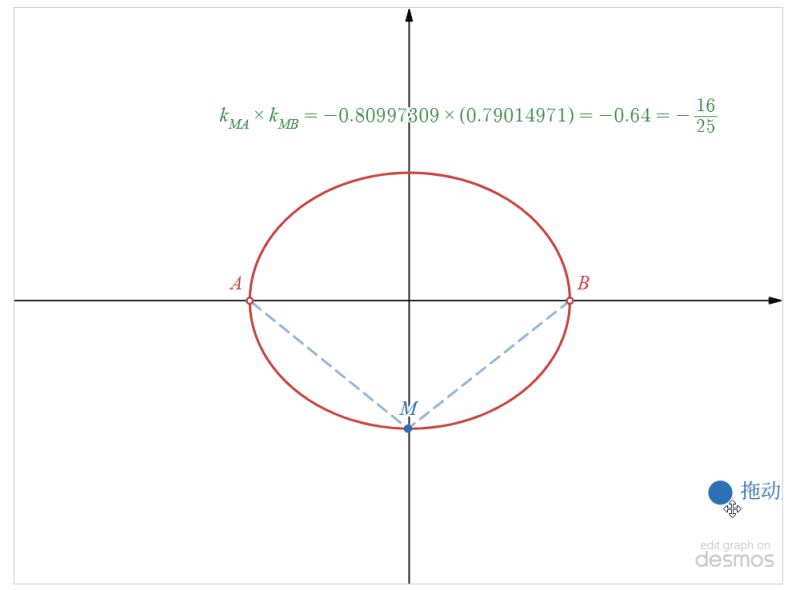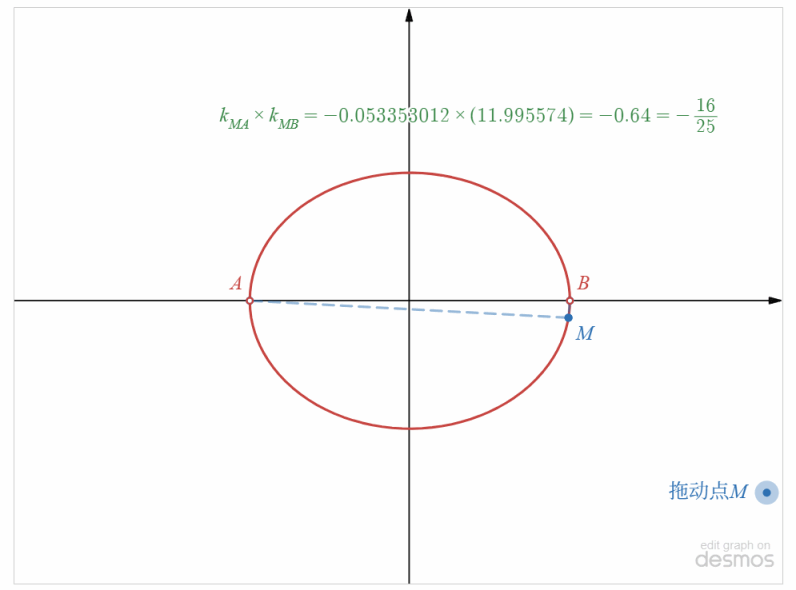
即所求的点 \(M\) 的轨迹方程为 \(\cfrac{x^2}{25}+\cfrac{y^2}{16}=1\),\(x\neq\pm 5\),所以点 \(M\) 的轨迹是以原点为中心,焦点在 \(x\) 轴上的椭圆(除去 \(A(-5,0)\) 和 \(B(5,0)\)两个点) .
关于课后习题的使用也来个例子
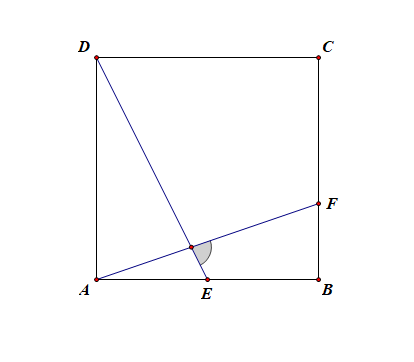
法1:基向量法,我们选向量 \(\overrightarrow{AB}\) 和向量 \(\overrightarrow{AD}\)作为基底向量,用它们来表示向量 \(\overrightarrow{DE}\) 和向量 \(\overrightarrow{AF}\),那么只要求解这两个向量的夹角,就能求得 \(\angle EMF\) .
由于 \(\overrightarrow{DE}\) \(=\) \(\cfrac{1}{2} \overrightarrow{AB}\) \(-\) \(\overrightarrow{AD}\) , 且 \(\overrightarrow{AF}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{3} \overrightarrow{AD}\),
所以,\(\overrightarrow{DE} \cdot \overrightarrow{AF}\)\(=\)\(\left(\cfrac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}\right)\)\(\cdot\)\(\left(\overrightarrow{AB}+\cfrac{1}{3} \overrightarrow{AD}\right)\) \(=\cfrac{1}{2} a^2-\cfrac{1}{3} a^2\) \(=\) \(\cfrac{1}{6} a^2\).
所以,\(\cos \angle EMF\)\(=\)\(\cfrac{\overrightarrow{DE} \cdot \overrightarrow{AF}}{|\overrightarrow{DE}||\overrightarrow{AF}|}\)\(=\)\(\cfrac{\cfrac{1}{6} a^2}{\cfrac{\sqrt{5}}{2} a \cdot \cfrac{\sqrt{10}}{3} a}\)\(=\)\(\cfrac{\sqrt{2}}{10}\)
法2:坐标法,建立如图所示的直角坐标系.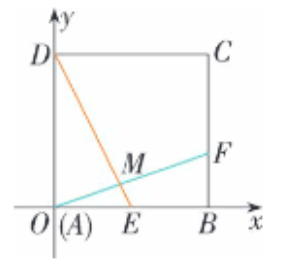
则 \(A(0,0)\)、 \(D(0, a)\)、 \(E(\cfrac{1}{2}a, 0)\)、\(F(a, \cfrac{1}{3} a)\)
则 \(\overrightarrow{DE}=\left(\cfrac{1}{2} a,-a\right)\),\(\overrightarrow{AF}=\left(a, \cfrac{1}{3} a\right)\),
\(\overrightarrow{DE} \cdot \overrightarrow{AF}=\cfrac{1}{2} a^2-\cfrac{1}{3} a^2=\cfrac{1}{6} a^2\),
\(|\overrightarrow{D E}|=\sqrt{\left(\cfrac{1}{2} a\right)^2+(-a)^2}=\cfrac{\sqrt{5}}{2} a\),\(|\overrightarrow{A F}|=\sqrt{a^2+\left(\cfrac{1}{3} a\right)^2}=\cfrac{\sqrt{10}}{3} a\),
\(\cos \angle E M F=\cfrac{\overrightarrow{DE} \cdot \overrightarrow{AF}}{|\overrightarrow{DE}||\overrightarrow{AF}|}=\cfrac{\cfrac{1}{6} a^2}{\cfrac{\sqrt{5}}{2} a \cdot \cfrac{\sqrt{10}}{3} a}=\cfrac{\sqrt{2}}{10}\)
法3:三角函数法,为简单起见,令正方形棱长为 \(1\),故 \(AB=1\), \(BF=\cfrac{1}{3}\), \(AE=\cfrac{1}{2}\),
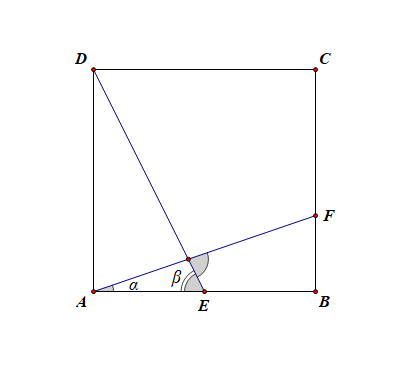
则 \(\tan\alpha=\cfrac{1}{3}\) ,\(\tan\beta=2\),故 \(\tan\theta=\tan(\alpha+\beta)=\cfrac{\cfrac{1}{3}+2}{1-\cfrac{1}{3}\times2}=7\),
由 \(\tan\theta=7\),令 \(\sin\theta=7k\), 则 \(\cos\theta=k\),\(k>0\),
由 \((7k)^2+k^2=1\),则 \(k^2=\cfrac{1}{50}\),
故 \(\cos\theta=k=\cfrac{1}{\sqrt{50}}=\cfrac{\sqrt{2}}{10}\);
自我结论
你说,按照这样的态度和方法,你认为刷教材上的习题还有作用吗 !

 用例子说明学习数学刷教科书上的题有没有用
用例子说明学习数学刷教科书上的题有没有用

 浙公网安备 33010602011771号
浙公网安备 33010602011771号