matlab基础
clear:清除工作空间的所有变量
clf:关闭所有的图形窗口
clc:清除命令窗口的内容,对工作环境中的全部变量无任何影响
inf:无穷大
nan:无法定义,即非数,如0/0
pathtool:自定义路径
real() 复数的实部
imag() 复数的虚部
abs() 实数的绝对值或复数取模
angle() 复数的辐角
conj() 复数的共轭
创建基础矩阵
zeros(m,n) 产生m*n的全0数组
ones(m,n) 产生m*n的全1数组
eye(m,n) 产生m*n的单位数组
rand(m,n) 产生m*n的均匀分布数组
randn(m,n) 产生m*n的正态分布数组
magic(n) 产生n*n的模仿数组
round() 四舍五入到最近的整数
fix() 向0方向取整数
floor() 向负无穷方向取整数
ceil() 向正无穷方向取整数
字符串操作
upper() 把字符串任一小写字母转换为大写字母
lower() 把字符串任一大写字母转换为小写字母
double() 转换字符串为ASCALL码
char() 将ASCALL码转换为字符串
int2str() 将整数转换为字符串
num2str() 将数值转换为字符串
str2num() 将字符串转换为数值
sprintf() 按照给定格式将数值转换为字符串
sscanf() 按照给定格式将字符串转换为数值
起始值:间隔:终止值
>> 1:0.1:2 ans = 1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
linspace(起始值,终止值,值的个数)
>> linspace(1,2,11) ans = 1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
矩阵:
创立矩阵(例三阶魔方矩阵)
>> a=magic(3) a = 8 1 6 3 5 7 4 9 2
矩阵特征值与特征向量
[X,D]=eig(a) X的每一列为对应的特征向量,D的对角线为矩阵的特征值
>> [X,D]=eig(a) X = -0.5774 -0.8131 -0.3416 -0.5774 0.4714 -0.4714 -0.5774 0.3416 0.8131 D = 15.0000 0 0 0 4.8990 0 0 0 -4.8990
逆矩阵
>> inv(a) ans = 0.1472 -0.1444 0.0639 -0.0611 0.0222 0.1056 -0.0194 0.1889 -0.1028
行列式
>> det(a) ans = -360
矩阵的秩
>> rank(a) ans = 3
转置矩阵
>> a' ans = 8 3 4 1 5 9 6 7 2
行最简式
>> rref(a) ans = 1 0 0 0 1 0 0 0 1
数据的拟合与插值:
tic %计时
%数据的拟合
clear all,clc
%确定x,y的坐标
figure(1)
x=0:0.1:1;
y=[1.2,1.6,1.67,3.6,4,5.3,5.6,7.6,7.7,8.3,8.5];
p1=polyfit(x,y,1) %线性拟合
y1=poly2str(p1,'x') %化为标准多项式形式
p2=polyfit(x,y,2) %二阶多相似拟合
y2=poly2str(p2,'x') %化为标准多项式形式
subplot(1,3,1),plot(x,y,'r-');title('原图')
subplot(1,3,2),plot(x,p1(1)*x+p1(2),'b-');title('线性拟合')
subplot(1,3,3),plot(x,p2(1)*x.^2+p2(2)*x+p2(3),'b-');title('二阶线性拟合')
%数据的插值
%linear:线性插值,matlab默认此插值方式
%nearnest:最近邻近插值法
%cubic:立方插值法
%spline:三次样条插值法
figure(2)
x=linspace(0,5,6);y=sin(x);%创建原始数据点
subplot(2,2,1),plot(x,y,'r-');title('原图')
x0=linspace(0,5,21); %待插值点
y0=sin(x0); %精确值
y1=interp1(x,y,x0); %线性插值法
subplot(2,2,2),plot(x0,y1,'b-');title('线性插值')
y2=interp1(x,y,x0,'spline')%三次样条插值法
subplot(2,2,3),plot(x0,y2,'g-');title('三次样条插值')
y3=interp1(x,y,x0,'cubic') %立方插值法
subplot(2,2,4),plot(x0,y3,'m-');title('立方插值')
disp('三种插值的残差为')
err=[y1-y0;y2-y0;y3-y0]
disp('残差的标准方差')
s=[std(err(1, : )),std(err(2, : )),std(err(3, : ))]
toc
符号计算:
创建符号变量:sym(常量,参数)
例:a=sym('pi+2*cos(3)'),
syms x; a=6*x^3
精度控制:
digits(5); %定义精度
a=vpa(sqrt(2)); %a=1.4142
极限:
limit(f,x,a,right):自变量x从右边趋近于a时,符号函数f的极限值
limit(f,x,a,left):自变量x从左边趋近于a时,符号函数f的极限值
符号微分:diff(f,y,x):矩阵f对于y的x阶级导数
clear,clc,syms a x y f=[a,y^3,y*cos(x),log(x)]; %创建矩阵 dfdx=diff(f) %对x的一阶导数 dfdy2=diff(f,y,2) %对y的二阶导数 dfdxd=diff(diff(f,x),y) %混合求导 dfdx = [ 0, 0, -y*sin(x), 1/x] dfdy2 = [ 0, 6*y, 0, 0] dfdxd = [ 0, 0, -sin(x), 0]
符号积分:s=int(f,v,a,b):f关于变量v的积分,积分区间在[a,b],缺少v时系统自动认定
clear,clc,syms x a p positive s1=int(a^x*cos(x),0,pi) %0到pi上的定积分 s2=int(1/x^p,1,inf) %1到无穷的定积分 s1 = -(log(a)*(a^pi + 1))/(log(a)^2 + 1) s2 = piecewise(1 < p, 1/(p - 1), p <= 1, Inf)
符号替换:subs(S,OLD,NEW) 表示将符号表达式S中的符号变量OLD替换为新的值NEW
clear,clc,syms x y s=x^2+3*x subs(s,x,y) s = x^2 + 3*x ans = y^2 + 3*y
符号累和:symsum(expr,v,a,b)
clear,clc,syms v f a=1;b=100; f=v^2; s=symsum(f,v,a,b) s = 338350
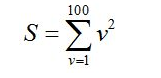
数值微分:
f(x)在x点的偏导数定义为:f‘(x)=lim(h->0) (f(x+h)-f(x))/h
方式一:
daoshu=diff(a,n,dim)
a:矩阵a n:n阶差分 dim=1时列计算,dim=2时行计算,默认dim=1
方式二:
二维情况:[dfdx,dfdy]=gradient(f,dx,dy)
其中didf为其水平方向上的梯度,dify为其垂直方向上的梯度
一维情况:didx=gradient(f,a)
f为矩阵 a为对应x 返回一维数值梯度
clear all,clc dt=pi/20; %定义dt,保证数值较小 t=pi/20:dt:pi/2; %x的取值 x=exp(t).*cos(t); %创建函数x=e^t * cos(t) dxdt_diff=diff(x)/dt %方式一计算 dxdt_grad=gradient(x,dt) %方式二计算 dxdt_diff = 0.9321 0.7975 0.5672 0.2191 -0.2701 -0.9243 -1.7666 -2.8178 -4.0943 %方式一结果 dxdt_grad = 0.9321 0.8648 0.6824 0.3931 -0.0255 -0.5972 -1.3455 -2.2922 -3.4561 -4.0943 %方式二结果
数值积分:
方式一:
[I,n]=quad(fun,a,b,tol)
计算被积函数fun在[a,b]上的定积分。输出变量I为定积分的结果,n为本积分的函数调用次数,tol为精确度,默认为10^-6
方式二:
[I,n]=quadl(fun,a,b,tol)
特性基本同上,该函数可以更精确的求出定积分的值。
quad:采用递推自适应的Simpson法来计算
quad1:采用递推自适应的Lobatto法来计算
方式三:
st=trapz(x,y)
其中x,y是基础数值,x可以为行向量或列向量,y可以为向量或矩阵,y的行数应等于x向量的元素个数;若dim=1,则按行求积,若dim=2,则按列求积。默认dim=1.
clear,clc format long %精度显示,计算sqrt(1-1/2*sinx)在0到pi/2上的定积分 [s_quad,n]=quad('sqrt(1-1/2*sin(x))',0,pi/2,1e-11) %方式一积分 [s_quadl,n]=quadl('sqrt(1-1/2*sin(x))',0,pi/2,1e-11) %方式二积分 s_quad = 1.288898992309974 %方式一结果 n = 121 %方式一被积函数调用次数 s_quadl = 1.288898992310102 %方式二结果 n = 48 %方式二被积分函数调用次数
clear,clc x=linspace(0,pi/2,500); %0到pi/2之间创建500个等间隔数值 y=sqrt(1-1/2*sin(x)); %同样,这是500个y的数值的行向量 s_trapz=trapz(x,y) %方式三积分 s_trapz = 1.288899198751829 %方式三结果
matlab解方程组:
多项式求跟:z=roots(p) 如果已知多项式的跟x,可以使用poly:p=poly(x)
clear,clc %求f(x)=2x^4+3x^2+2x-5全根 p=[2 0 3 2 -5]; x=roots(p) %求全根 g=poly(x); %构造新多项式 g=poly2str(g,'x') x = 0.141441321334151 + 1.592960474043117i 0.141441321334151 - 1.592960474043117i -1.140196435014263 + 0.000000000000000i 0.857313792345960 + 0.000000000000000i g = ' x^4 - 2.2204e-16 x^3 + 1.5 x^2 + 1 x - 2.5'
线性代数方程组(齐次):
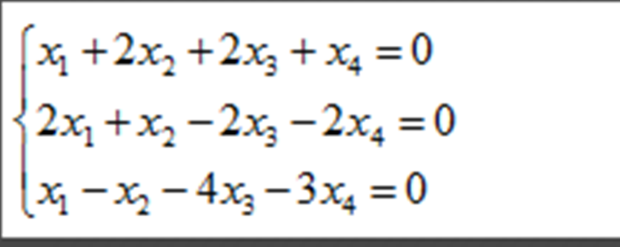
clear,clc a=[1 2 2 1;2 1 -2 -2;1 -1 -4 -3]; format rat %结果用有理分数显示 z=null(a,'r') %方程的通解如下 syms k1 k2 x=k1*z( : ,1)+k2*z( : ,2) z = 2 5/3 -2 -4/3 1 0 0 1 x = 2*k1 + (5*k2)/3 - 2*k1 - (4*k2)/3 k1 k2
(非齐次)
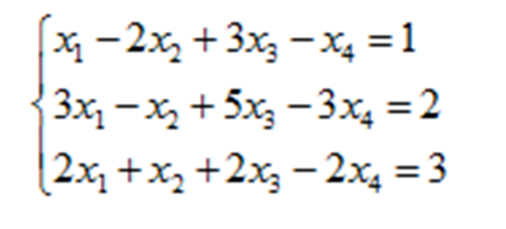
clear,clc A=[1 -2 3 -1;3 -1 5 -3;2 1 2 -1]; b=[1 2 3]'; B=[A b]; n=4; %未知数的个数 ra=rank(A); rb=rank(B); format rat if ra==rb&ra==n x=A\b elseif ra==rb&ra<n x=A\b z=null(A,'r') else x='无解' end x = 0 9/7 13/7 2 z = -7/5 4/5 1 0
符号方程solve:
clear,clc syms x y eq1=3*x+6*x-4; s1=solve(eq1,x) eq2=y-5*y-8; s2=solve(eq2,y) s1 = 4/9 s2 = -2




 浙公网安备 33010602011771号
浙公网安备 33010602011771号