用位运算实现加减乘除(2)
位运算实现除法
先说一种普遍的除法,比如下图中的a / b:
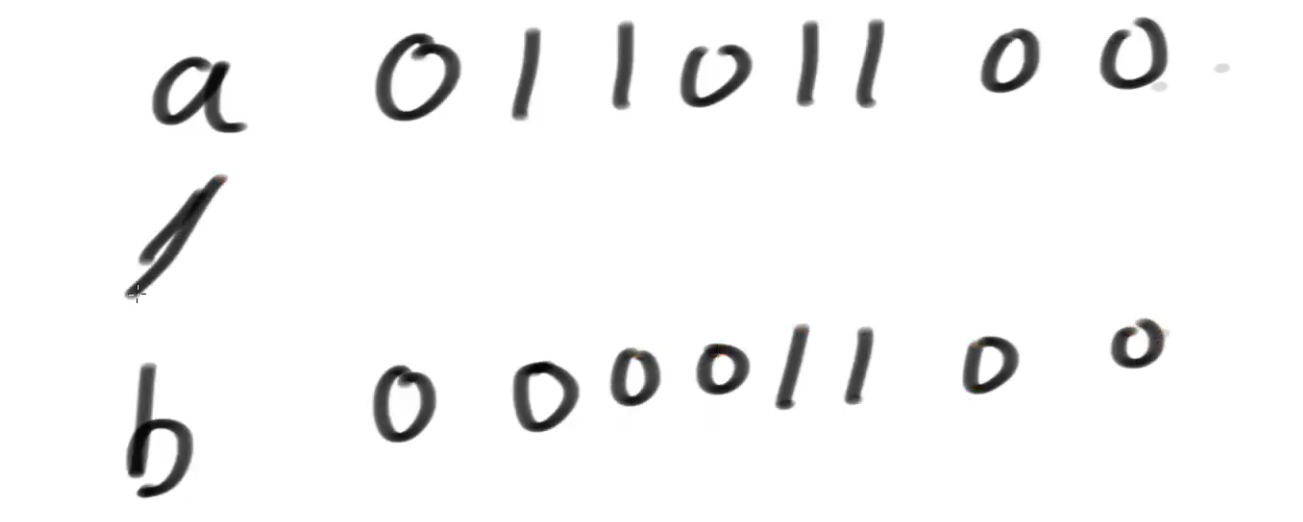
b向左移到最接近a的时候,但是又没a大,要保证左移到最接近a但是不比a大。
除的最终结果里,这个位置一定有1,见下图:
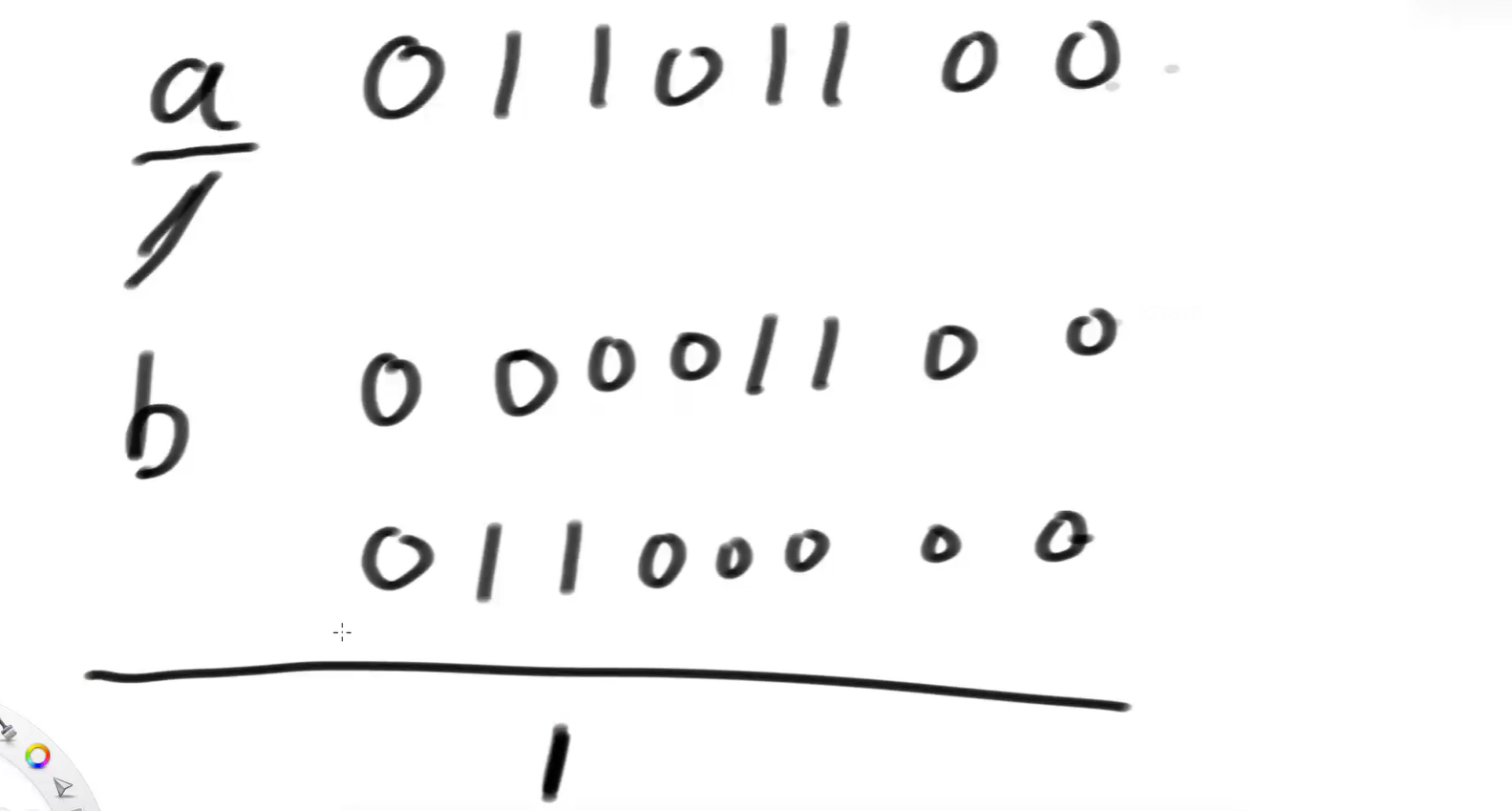
然后把a减掉这个数,变成:
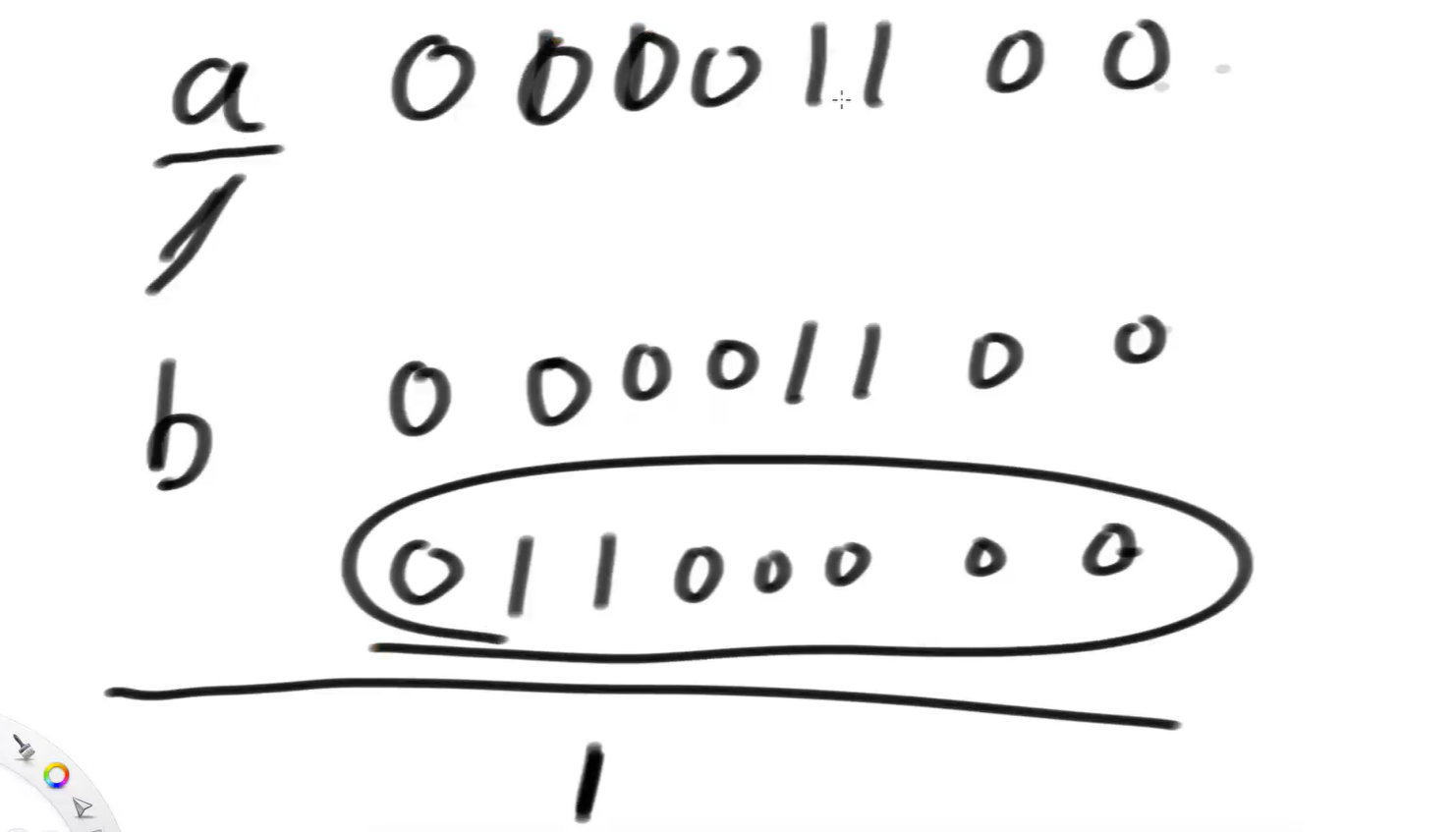
然后再把b移动到最接近a的时候,这个位置一定是1:

这就是最终的结果:
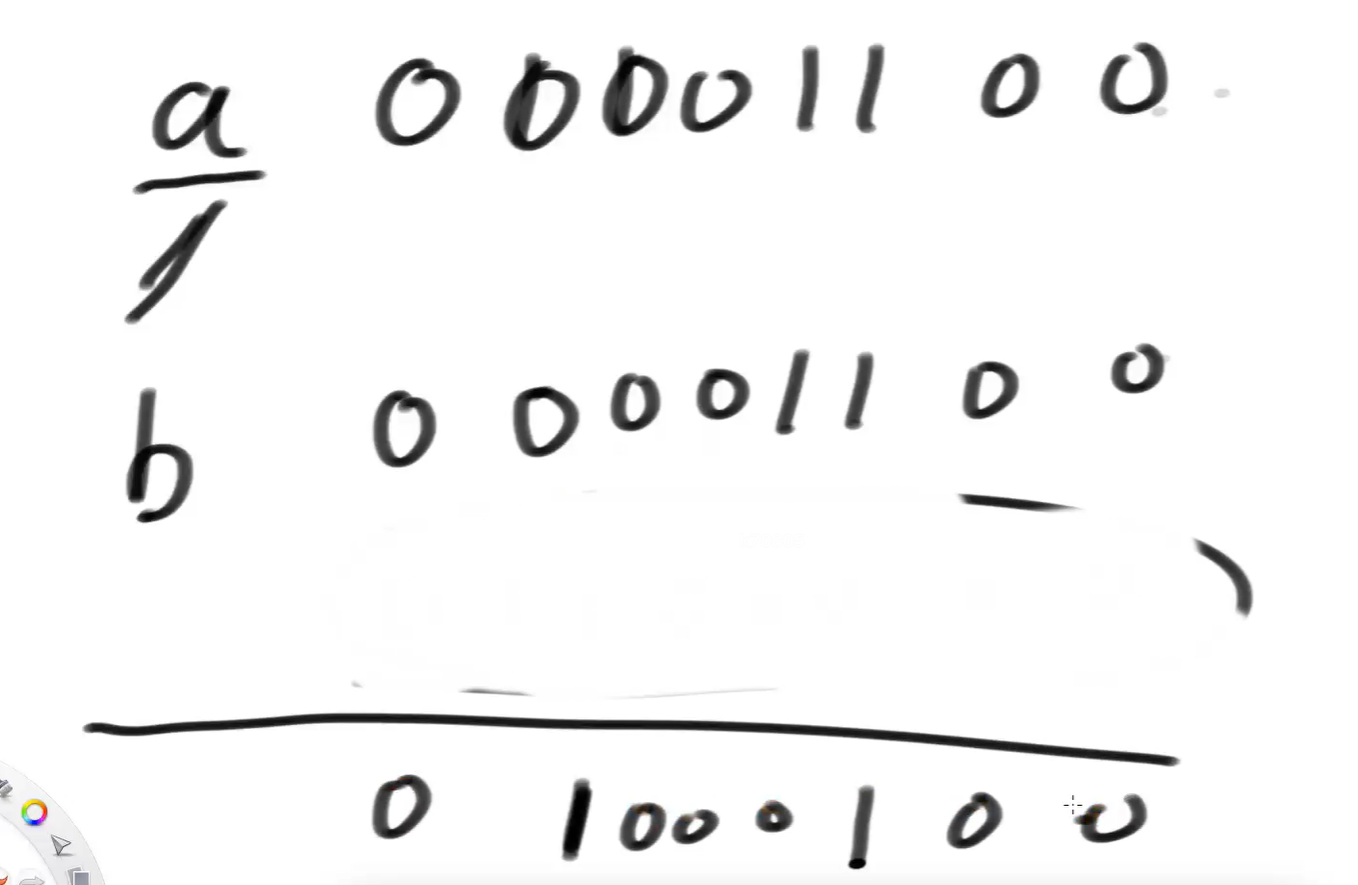
a/b的过程就是上面的。如果不太好理解的话,看下面这种解释:
如果a / b = c,如图:
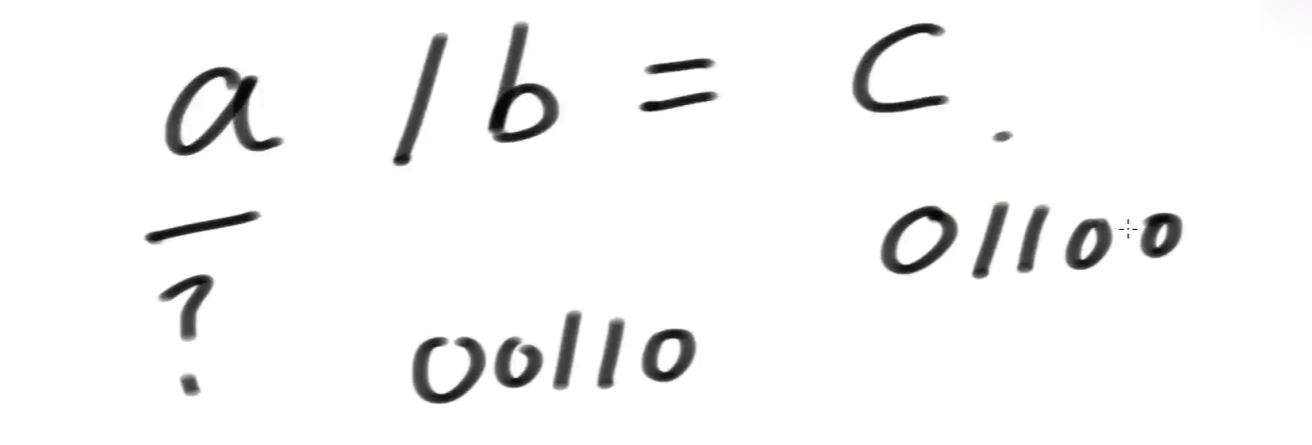
说明啥?a可以这么表示:

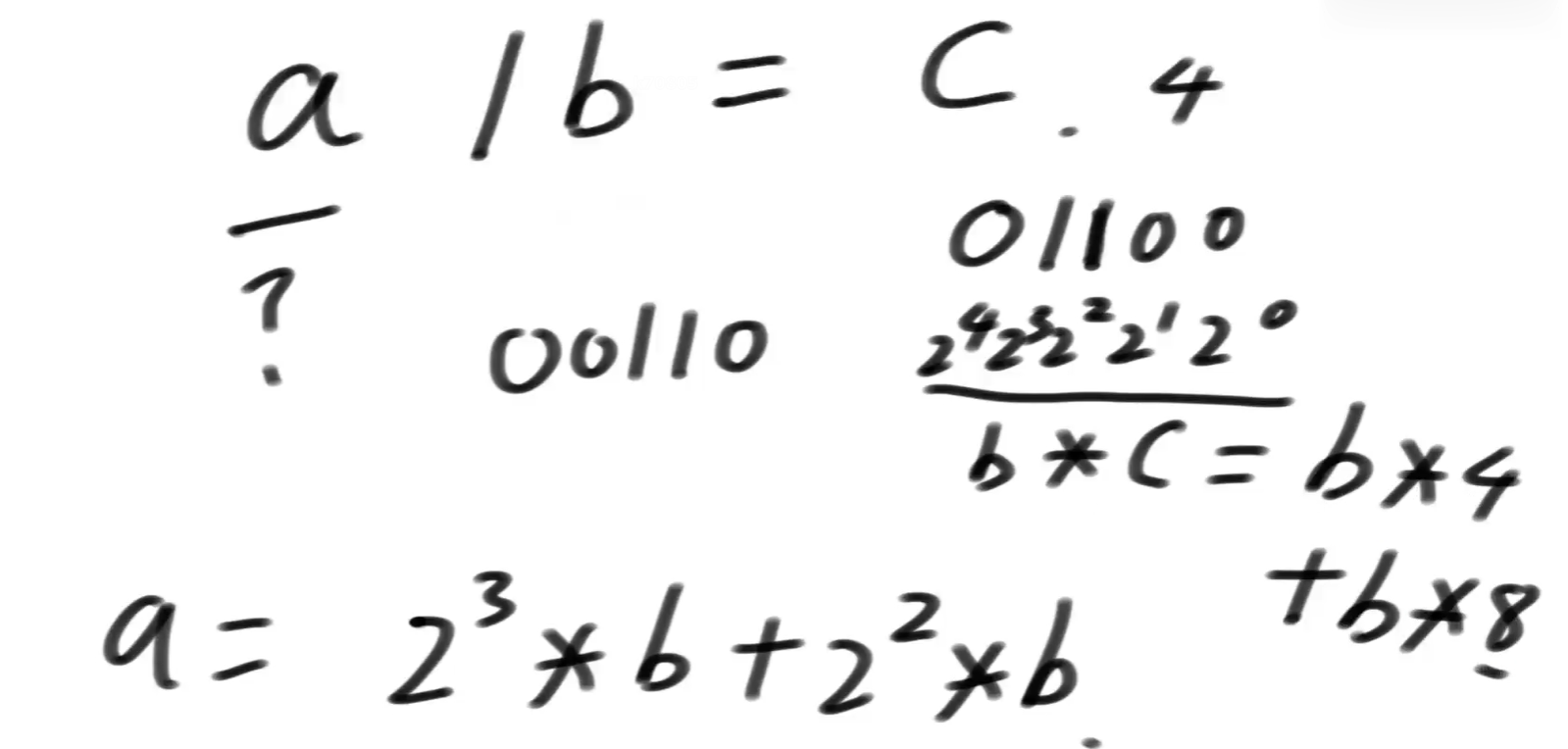
再举个例子:
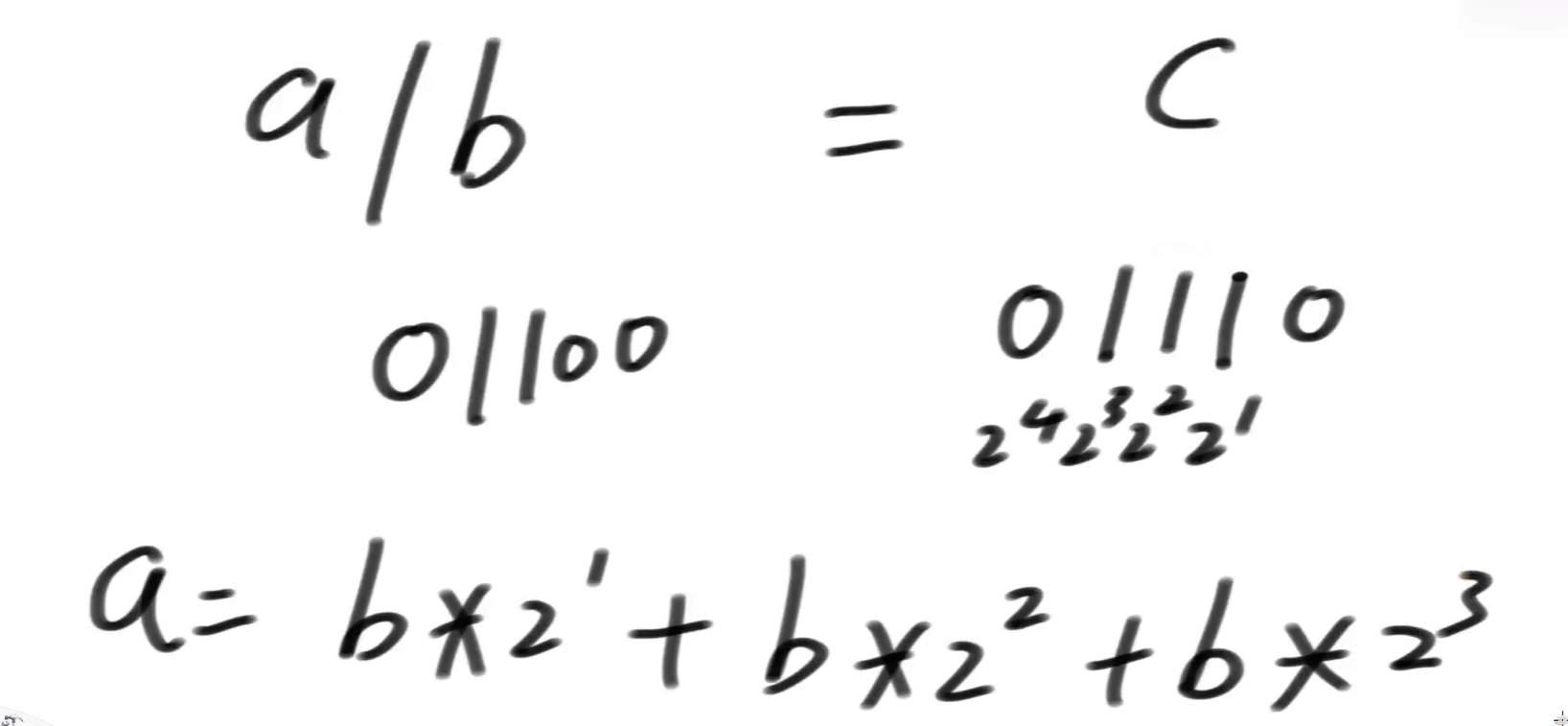
看到上面的例子,那我们应该怎么做?
怎么求这个c呢?这么想:
a - 一个尽可能大的2某次方 * b = a'
a' - 一个尽可能大的2某次方 * b = a''
a'' - 一个尽可能大的2某次方 * b = a'''
...
一直这么减,就把结果得到了。
b*c的演算过程:
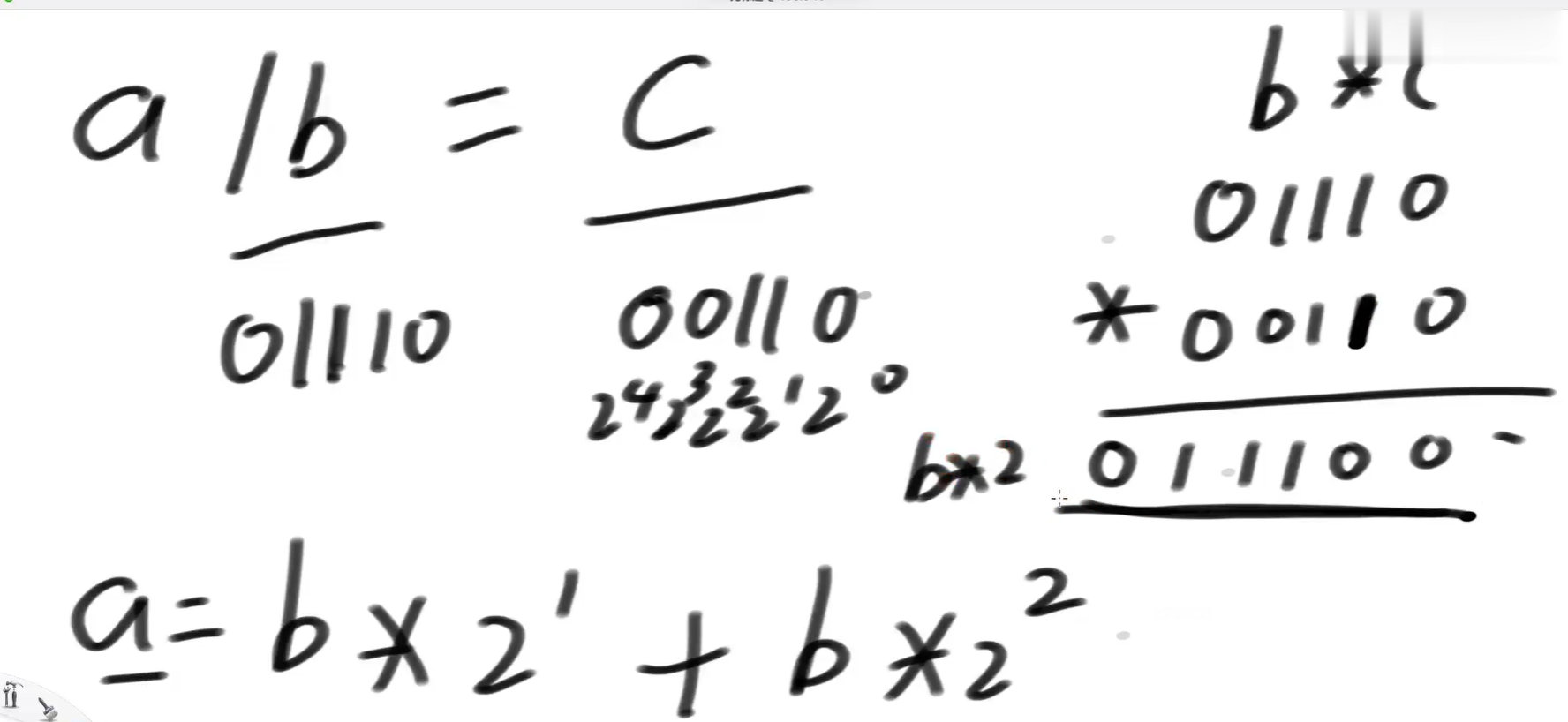
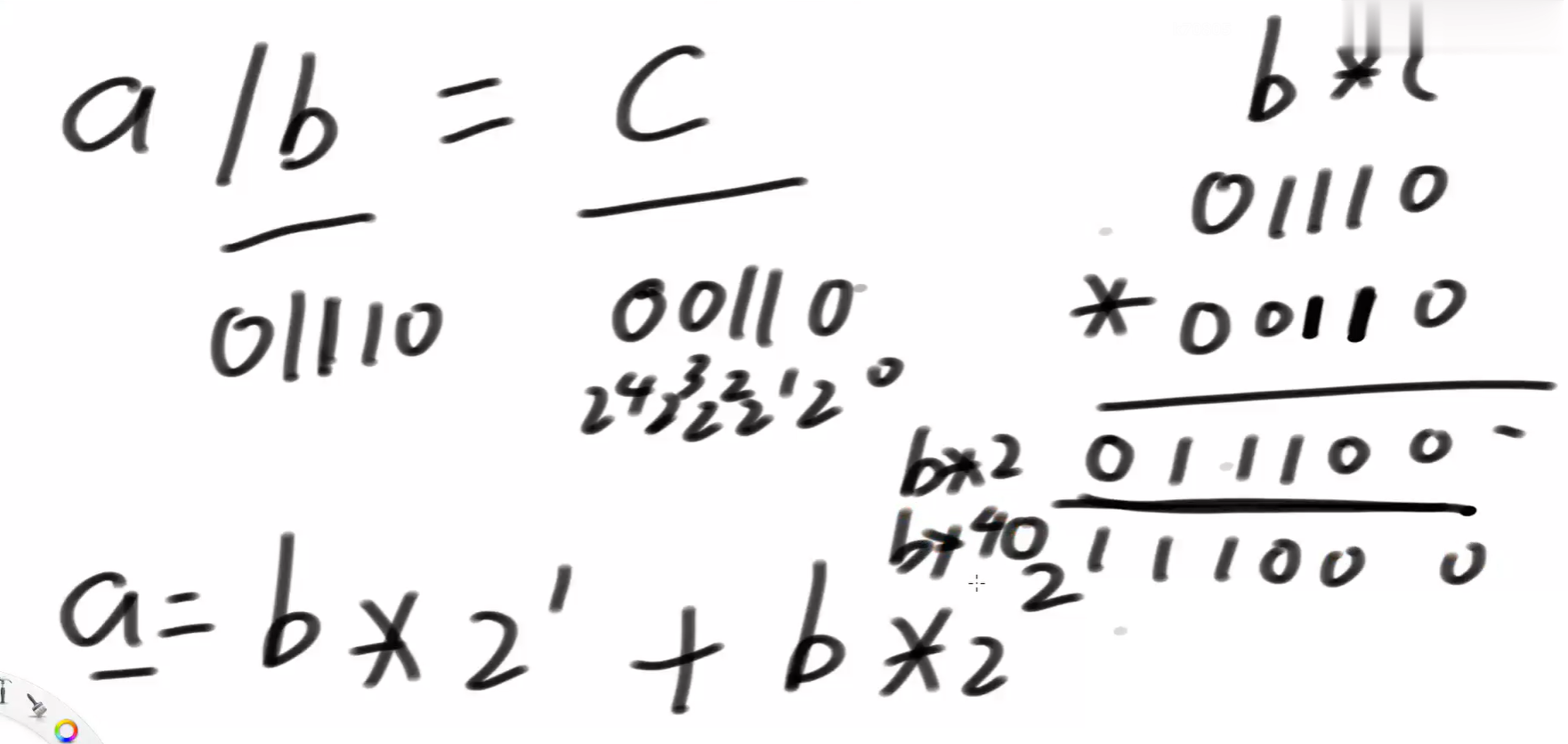

a = b * 2 + b * 2²,也就是 a = b << 1 + b << 2
假设,a = b*2⁷ + b*2⁵ + b*2³,你说c是啥?在第7、5、3位置上是1,其他都是0 :

所以,怎么算a/b呢?
a我先看看,最大的2的某次方 * b,而且2ⁿ*b不能超过a,找到最大2的某次方。假设是7,那么我就知道最终结果7的位置上一定是1。
a': a - b*2⁷,再次找到最接近a'的2某次方 * b,假设是5,那么我知道最终结果5的位置上一定是1。
a'': a' - b*2⁵, 再次找到最接近a''的2某次方 * b,假设是3,那么我知道最终结果3的位置上一定是1。
...
所以c就是 10101000
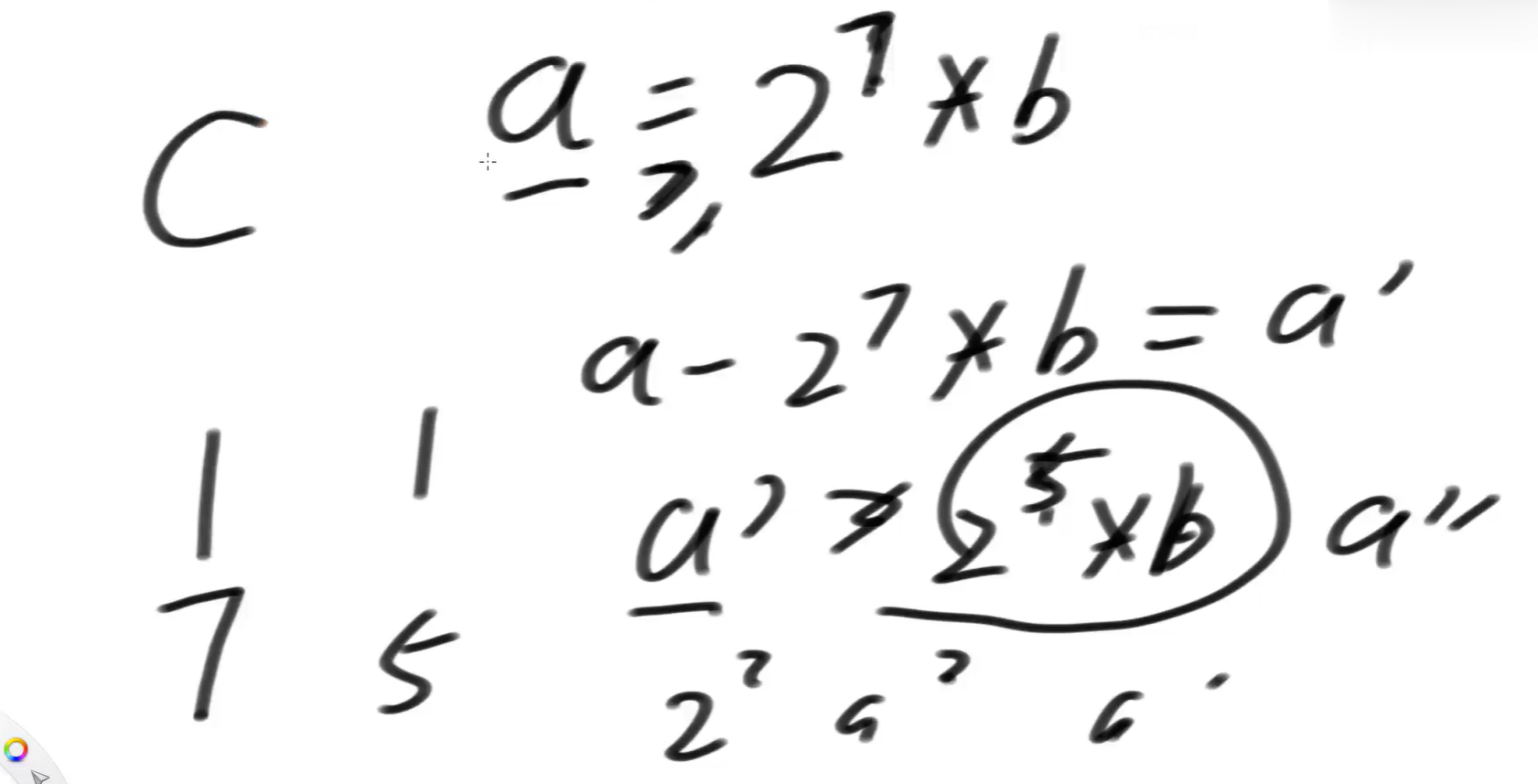
思路就是这样。具体如何操作?
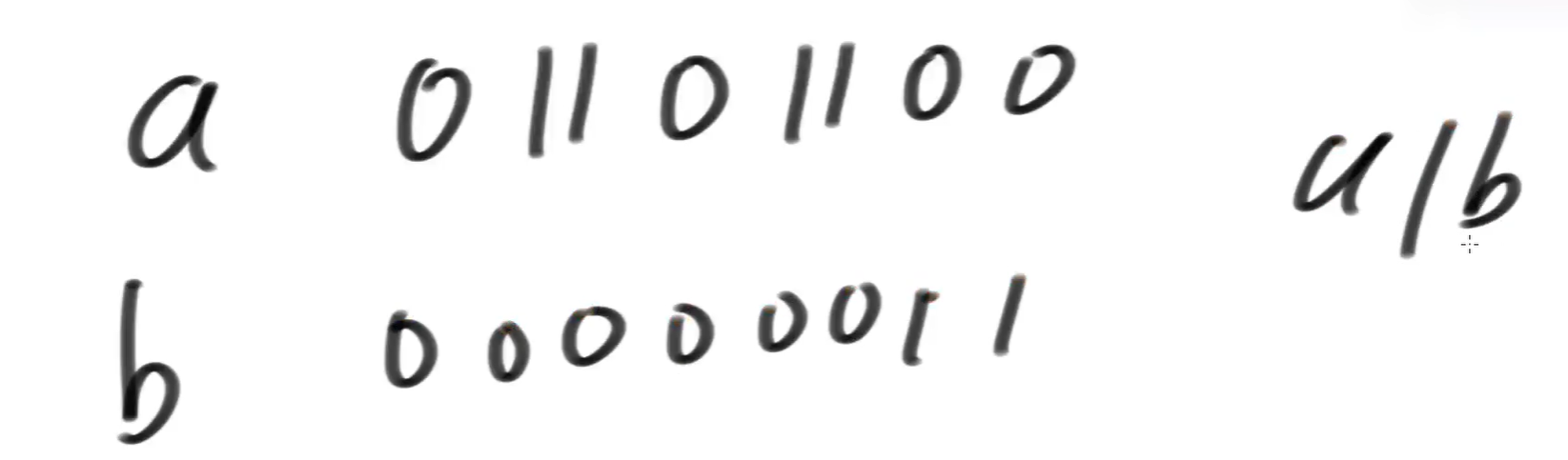
a/b等于几?
b离a最近的又不超过a的,左移了几位?5位。

然后a 减掉 这个数,再去看b左移几位然后不超过a刚好够的?左移2位。
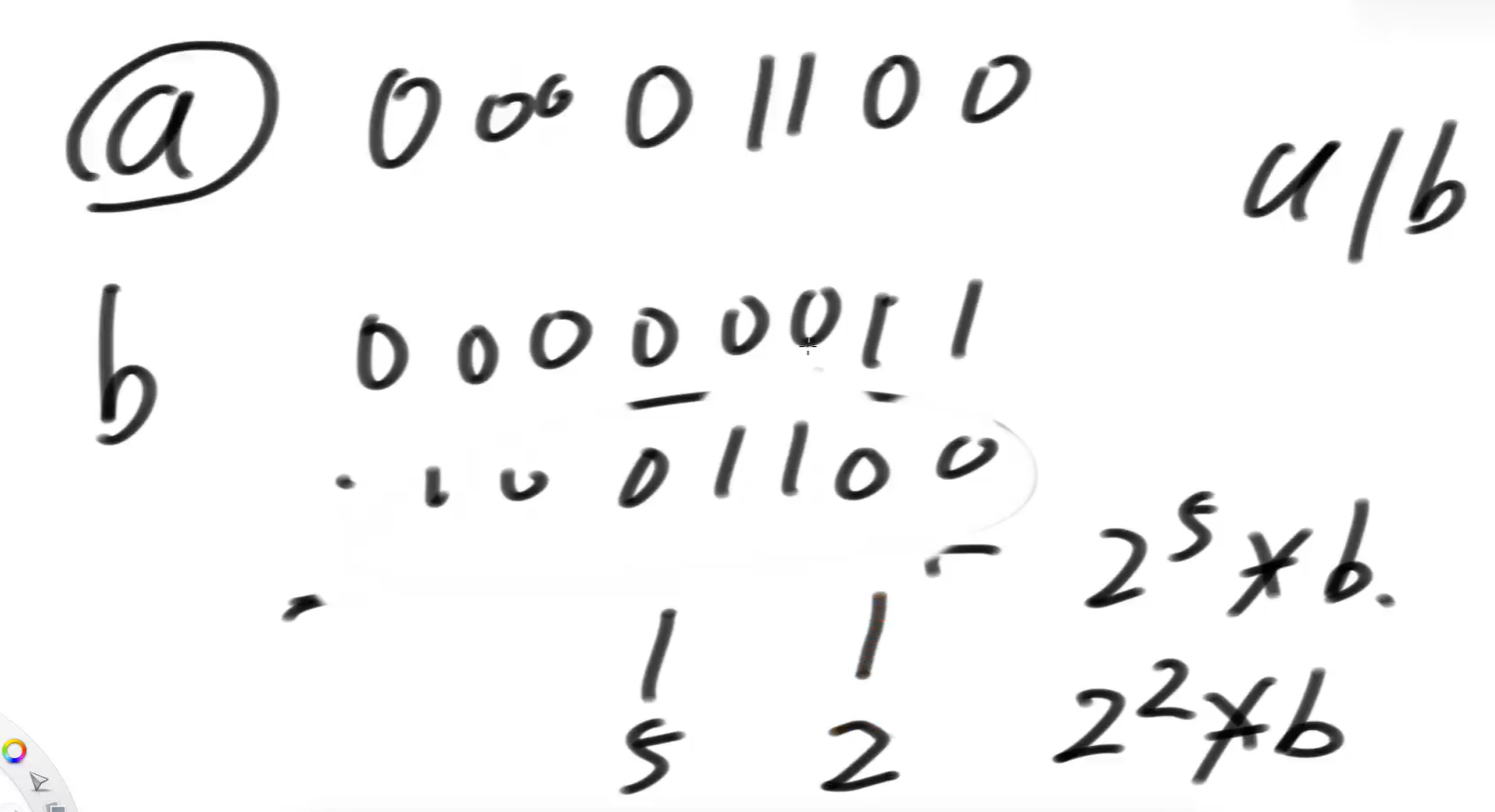
a再减掉这个数,等于0,结束。
a = b*2⁵ + b*2²,c就是:100100
代码实现:
package com.cy.class05;
/**
* 位运算实现+-*\\/
* 测试连接:https://leetcode.com/problems/divide-two-integers
*/
public class Code03_BitAddMinusMultiDiv {
public static int add(int a, int b) {
int sum = a;
while(b != 0) {
sum = a ^ b; //无进位相加信息 -> sum
b = (a & b) << 1; //进位信息 -> b -> b'
a = sum; //无进位相加信息a -> a'
}
return sum;
}
/**
* 返回n的相反数
* 相反数 = 取反 + 1
* -n = ~n + 1
*/
public static int negNum(int n) {
return add(~n, 1);
}
public static int minus(int a, int b){
return add(a, negNum(b));
}
/**
* 乘法
*
* 右移:
* b >> 1,表示右移1,最高位拿符号位来补。
* b >>>1, 表示右移1,最高位一律拿0来补。
*
* 支持负数,道理不好解释,负数的情况下到底发生了什么,跟补码有关,你只要知道同样这套方法既支持正数也支持负数。
*/
public static int multi(int a, int b) {
int res = 0;
while(b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a <<= 1;
b >>>= 1;
}
return res;
}
public static boolean isNeg(int n) {
return n < 0;
}
/**
* 除法
*
* 这个方法在正式开始之前,a和b一定要都转成正数
*
* x是非负的,第32位是符号位,肯定是0,所以没必要右移31位。所以for循环i从30开始。
*
* 这里^的运算是:非短路逻辑异或,两边的表达式都会执行
* boolean a = true, b = false;
* boolean c = a ^ b; // true(不同时为 true/false)
* 如果需要逻辑异或(对布尔没必要值),直接用 != 更直观: boolean xor = (a != b); // 等效于 a ^ b
*
* a ^ b: a和b不同返回true,否则返回false
*
* 这个除法必须要求x和y转成正数的形式。
* 这个方法一定是要能把a和b转成正数才能继续算,但系统最小值没办法转绝对值,所以有局限。
*/
public static int div(int a, int b) {
int x = isNeg(a) ? negNum(a) : a;
int y = isNeg(b) ? negNum(b) : b;
int res = 0;
// x / y
for (int i=30; i>=0; i = minus(i, 1)) {
if ((x >> i) >= y) {
res |= (1 << i);
x = minus(x, y << i);
}
}
//如果a和b符号不一样,取个负号返回;如果a和b负号一样,直接返回答案
return isNeg(a) ^ isNeg(b) ? negNum(res) : res;
}
public static void main(String[] args) {
int a = 7;
int b = -3;
System.out.println(multi(a, b));
}
}
div方法解释:
1.代码中是x/y,为什么看到x右移?y去够x,和x去够y,其实是一码事。
为什么是一码事,看图解:
y要左移几位才能够上x?3位。

同样道理,x往右移几位能让y勾上自己?右移3位,所以x往右移看什么时候能够上y,和y往左移看什么时候能够上x,是一码事。
为什么要让x往右移,因为y这个玩意,左移的话有可能移动到符号位上,就干了。
如下图,y左移的话,左移3位的话和x相等,要再左移1位才知道比x大了,才知道是左移3位。移4位的时候才知道上一位才是我应该来的位置,但要过一位才能判断出来,就有风险了。
而x往右移没这个风险。
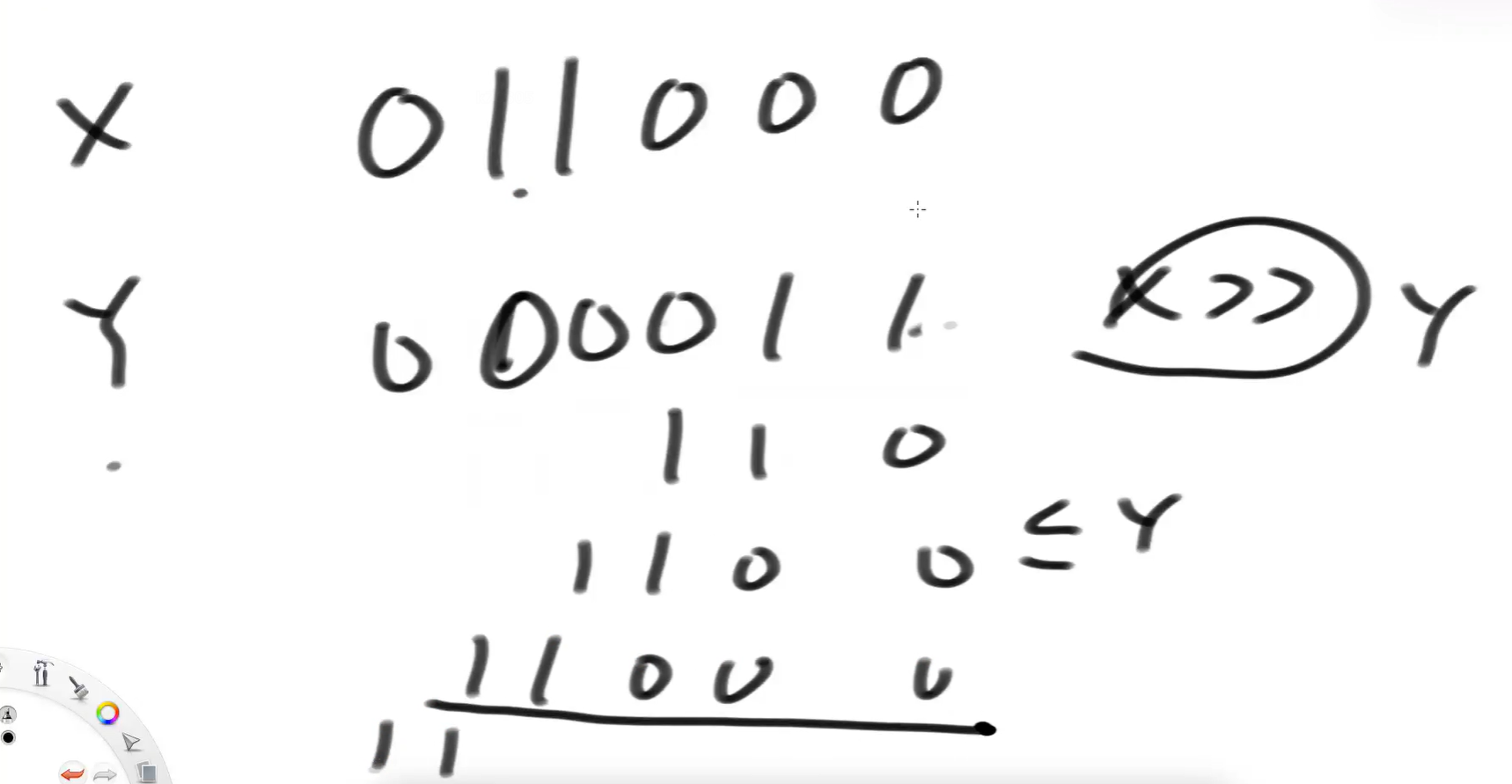
如下图,x是一个很大的数,y往左移去够x,左移n位正好等于x,但是还需要左移一位大于x了后才知道上一位是该来的位置,继续左移一位后到符号位了,y就变成负数了,还是不大于x啊。它还会左移,就会发生不可预知的错误。
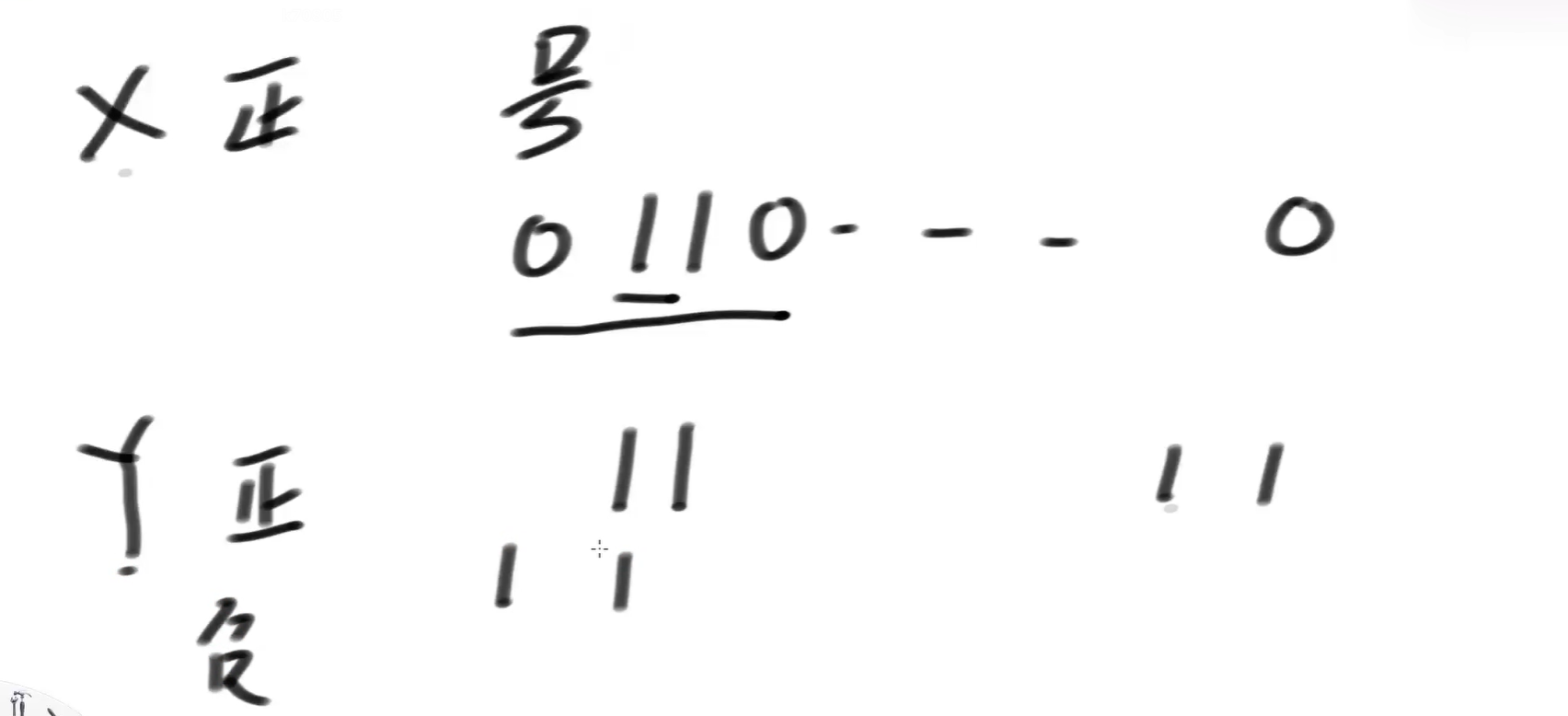
x这个数如果不大没什么问题。就怕它很大。


所以为了安全起见,让x去够y。右移不会牵扯到改符号位的问题。右移不会有溢出问题。
2.除不尽会怎样?比如9 / 4:
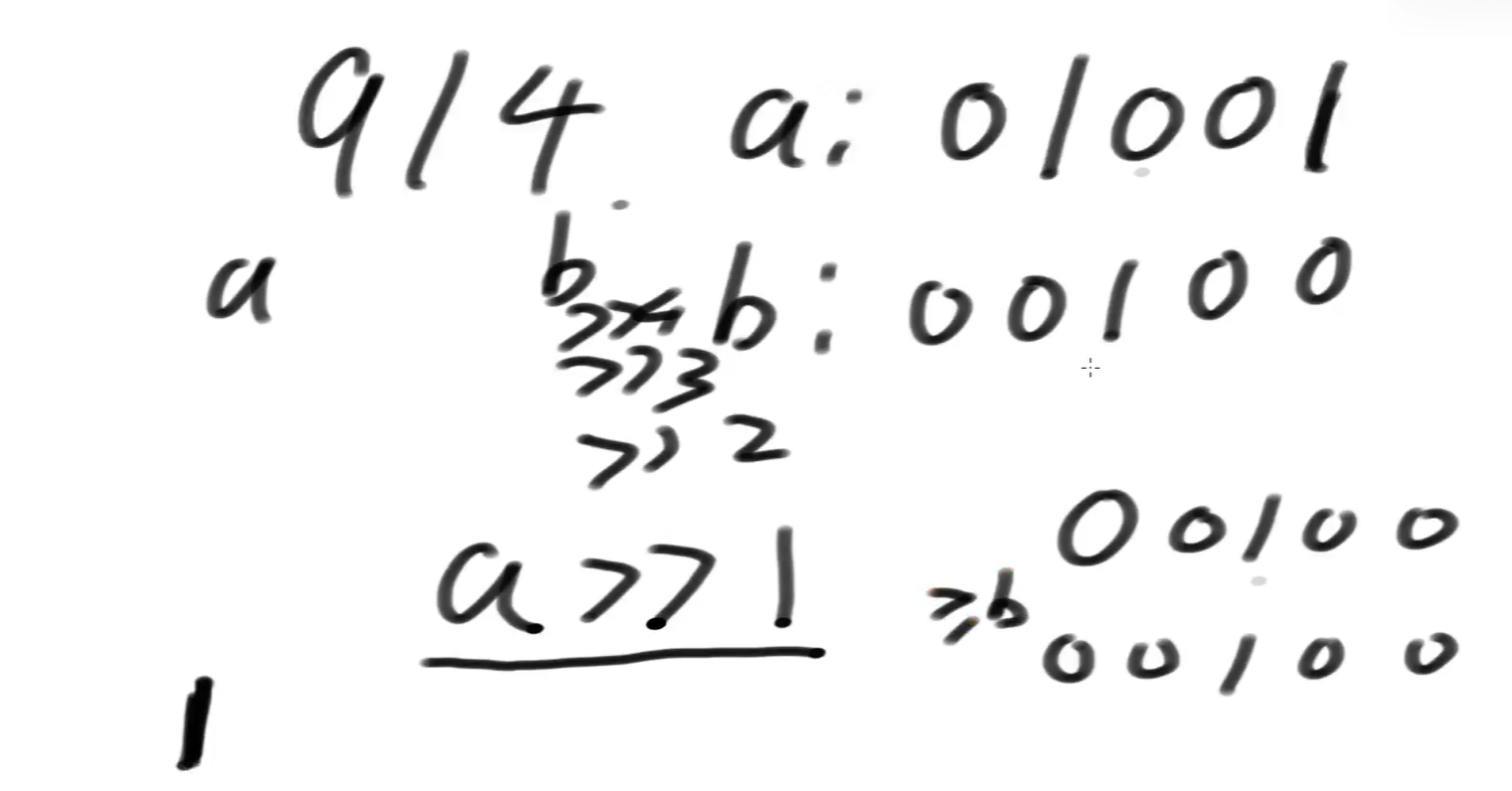
a - (b << 1)之后:
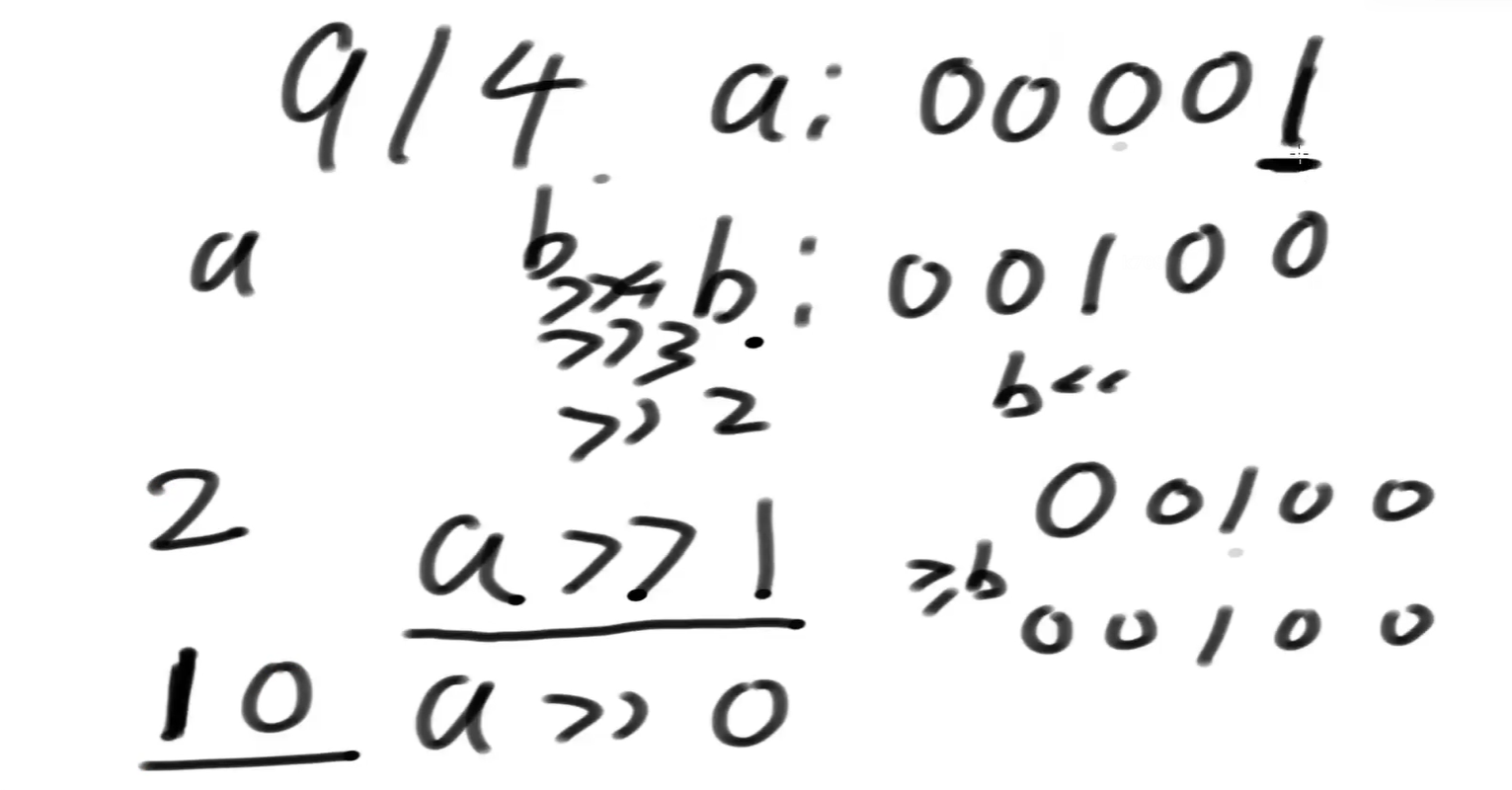
a>>0后,并不比b大,for循环结束。res 等于2进制的 10,返回2。所以div方法除不尽也没事。
--



 浙公网安备 33010602011771号
浙公网安备 33010602011771号