二分法
有序数组中找到num
有序数组中找到>=num最左的位置
有序数组中找到<=num最右的位置
局部最小值问题
有序数组中找到num:
当然你可以遍历,但是那就没意思了,你没有利用到有序这个条件。
二分法查找,代码如下:
查看代码
package com.cy.class03;
import com.cy.class02.Code03_Comp;
import java.util.Arrays;
/**
*
*/
public class Code01_BSExist {
/**
*
* 二分法查找
* arr保证是有序的
*/
public static boolean find(int[] arr, int num) {
if (arr == null || arr.length == 0) {
return false;
}
int L = 0;
int R = arr.length - 1;
// arr[0 .. N-1] num arr[L .. R] num
while(L <= R) {
int mid = (L + R) / 2;
if (arr[mid] == num) {
return true;
} else if (arr[mid] < num) {
L = mid + 1;
} else {
R = mid - 1;
}
}
return false;
}
/**
* 暴力测试,用于测试验证正确性,这个一定是正确的
*/
public static boolean test(int[] sortedArr, int num) {
for (int cur: sortedArr) {
if (cur == num) {
return true;
}
}
return false;
}
public static void main(String[] args) {
int[] arr = {4, 10, 16, 16, 46, 51, 54, 55, 61, 71, 74, 75, 77, 77, 82, 82, 84, 84, 85, 98, 99, 131, 133, 134, 139, 144, 145, 146, 150, 151, 167, 170, 189, 193, 199};
boolean exist = find(arr, 199);
System.out.println(exist);
}
}
有序数组中找到>=num最左的位置:
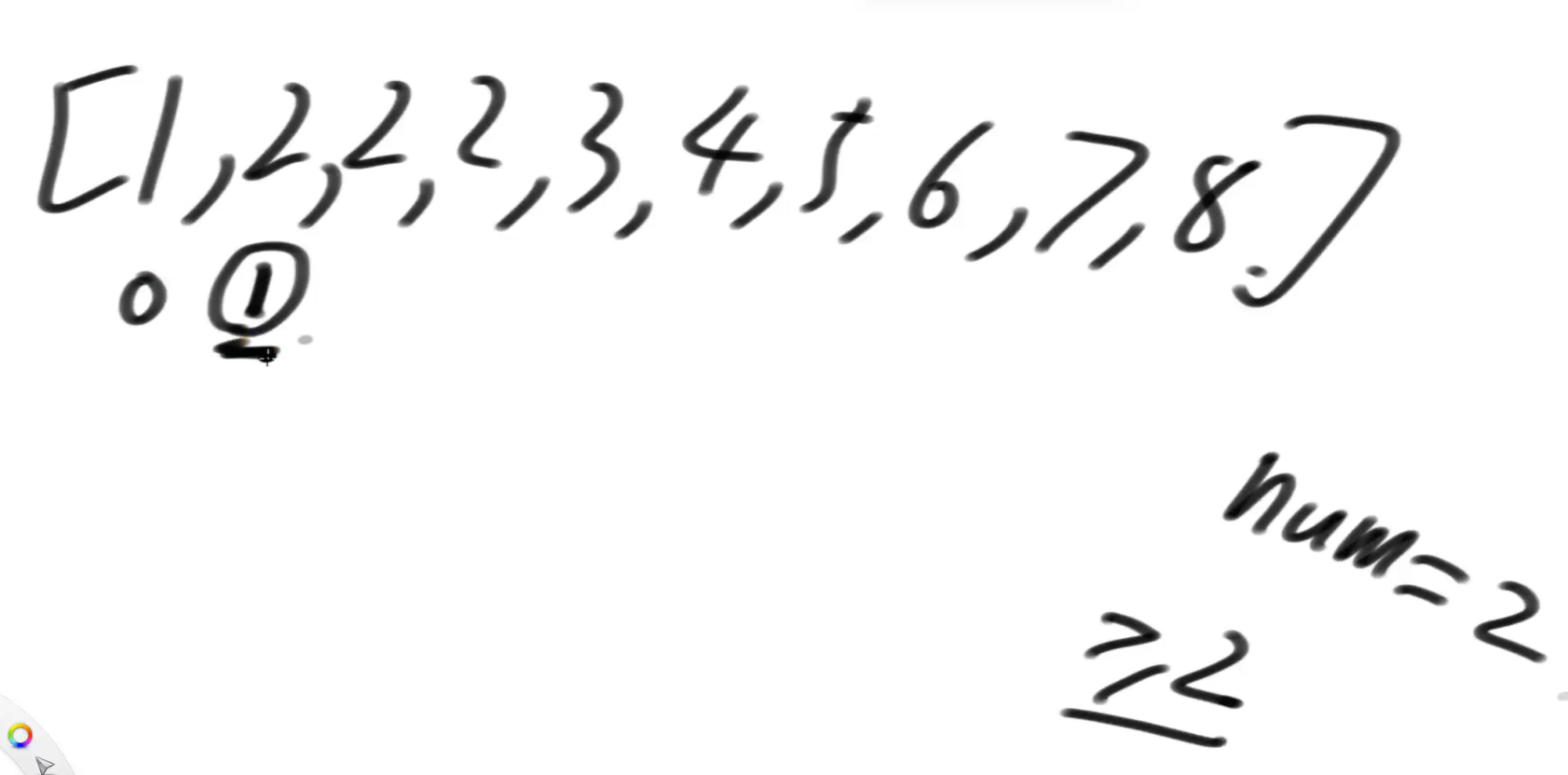
能不能继续二分?
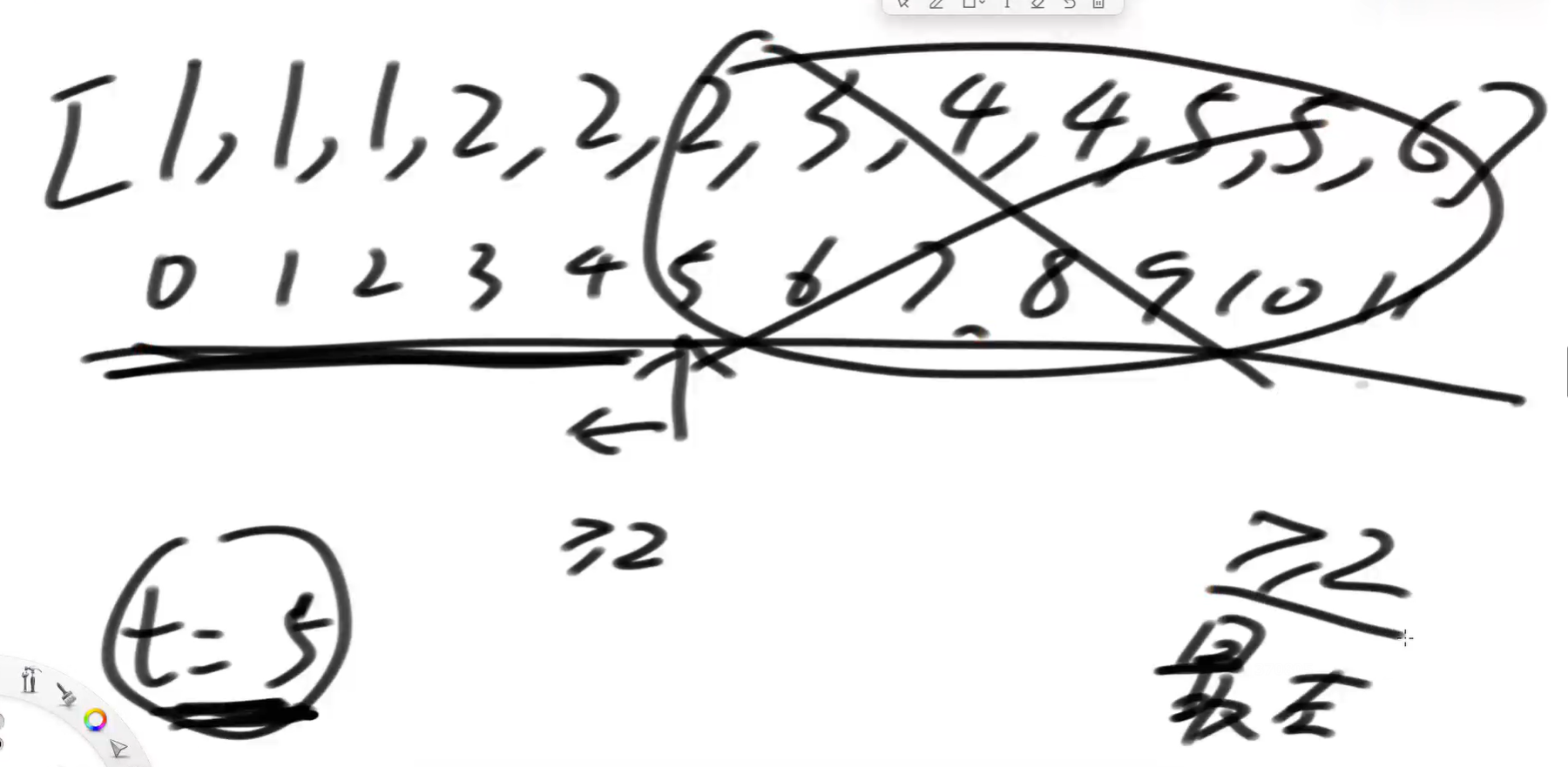
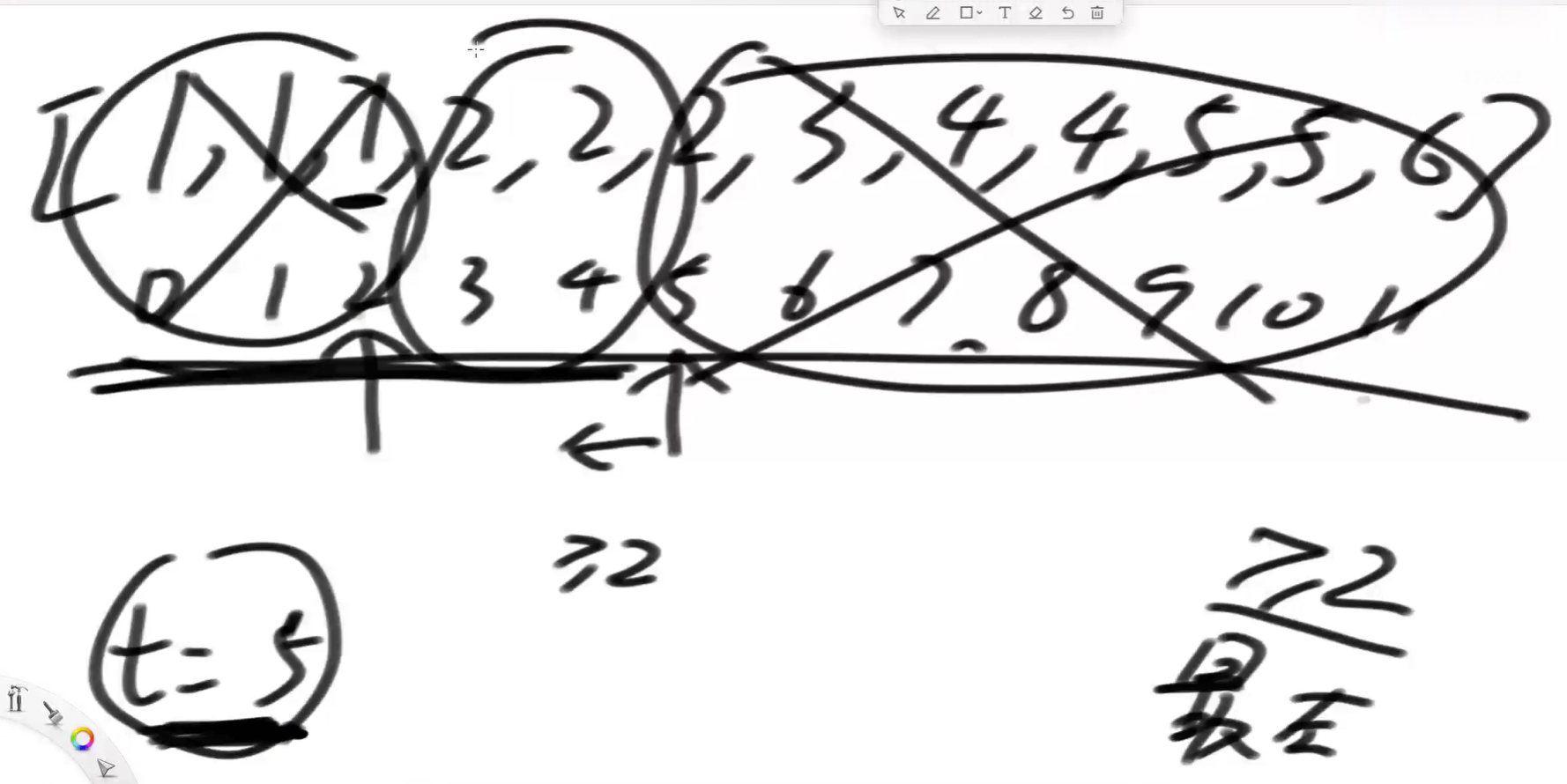
首先,从0~11,二分法查找,t=5的位置找到>=2的,所以现在至少有个t=5的位置是>=2的最左侧的位置;再往左还有没有>=2的呢?
不知道,继续试,从0~4继续找有没有>=2的?
0~4,打到中点位置2,值是1,不是>=2的,变量t就不更新;所以2的左边不会有>=2的;
在3~4的位置再试;中点位置3,值为2,是>=2的,t更新,从5变为3。
3的左边发现没数了,停止。t最晚抓到的数就是答案。
代码如下:
查看代码
package com.cy.class03;
import java.util.Arrays;
/**
* 有序数组中找到>=num最左的位置
*/
public class Code02_BSNearLeft {
/**
* arr有序, 找到>=num 最左的位置
*/
public static int mostLeftNoLessNumIndex(int[] arr, int num) {
if (arr == null || arr.length == 0) {
return -1;
}
int L = 0;
int R = arr.length - 1;
int t = -1; //记录最晚发生>=num的位置
while(L <= R) {
//t更新
int mid = (L + R) / 2;
if (arr[mid] >= num) {
t = mid;
R = mid - 1;
} else {
L = mid + 1;
}
}
return t;
}
// for test
public static int test(int[] arr, int value) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] >= value) {
return i;
}
}
return -1;
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 10;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr = generateRandomArray(maxSize, maxValue);
Arrays.sort(arr);
int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
if (test(arr, value) != mostLeftNoLessNumIndex(arr, value)) {
printArray(arr);
System.out.println(value);
System.out.println(test(arr, value));
System.out.println(mostLeftNoLessNumIndex(arr, value));
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
}
有序数组中找到<=num最右的位置:
查看代码
package com.cy.class03;
import java.util.Arrays;
/**
* 有序数组中找到<=num最右的位置
*/
public class Code03_NearRight {
public static int mostRightLessNumIndex(int[] arr, int num) {
int L = 0;
int R = arr.length - 1;
int t = -1; //记录最晚出现<=num的位置
while(L <= R) {
int mid = (L + R) / 2;
if (arr[mid] <= num) {
t = mid;
L = mid + 1;
} else {
R= mid - 1;
}
}
return t;
}
// for test
public static int test(int[] arr, int value) {
for (int i = arr.length - 1; i >= 0; i--) {
if (arr[i] <= value) {
return i;
}
}
return -1;
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 10;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr = generateRandomArray(maxSize, maxValue);
Arrays.sort(arr);
int value = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
if (test(arr, value) != mostRightLessNumIndex(arr, value)) {
printArray(arr);
System.out.println(value);
System.out.println(test(arr, value));
System.out.println(mostRightLessNumIndex(arr, value));
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
}
}
局部最小值问题
给定一个数组,无序,任意两个相邻的数不相等

最左边界,如果arr[0] < arr[1],那么0位置上的数为局部最小;
最右边界,如果arr[N-1] < arr[N-2],那么N-1位置上的数为局部最小;
中间位置,如果arr[i] < arr[i+1],且arr[i] < arr[i-1],那么i位置上的数为局部最小;
不要求所有局部最小都是什么,只要其中一个局部最小,你给我能返回就行。
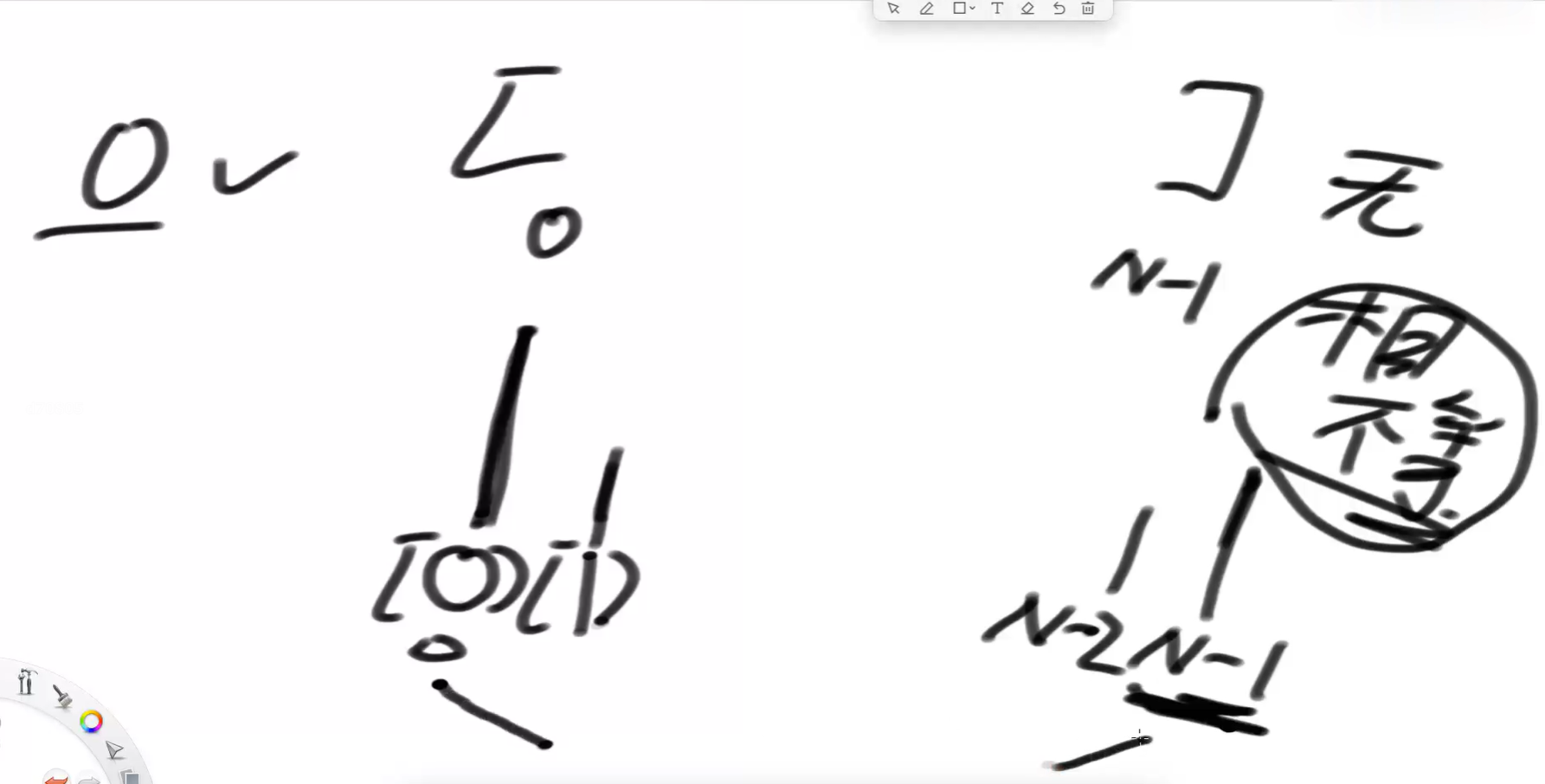


如果不是左边界,和右边界,上的数存在局部最小,可以看出曲线是先往下,出口的时候又变成了往上。
那么,0~N-1上必有局部最小。
从0~N-1上取中间值,mid,如果arr[mid] 比左边也小,比右边也小,正好是局部最小值,那么返回arr[mid]就行了。
如果arr[mid]不是局部最小:
就三种情况:
1.mid > mid-1, mid < mid + 1
2.mid < mid-1, mid > mid + 1
3.mid > mid-1, mid > mid + 1
假设mid左边比mid值小,这种情况又重现了,0位置>1位置,小局部是下降的,mid-1 < mid,小局部又是上扬的,断言0~mid上必有局部最小;
如果不符合假设,那么mid-1 > mid,由于mid不是局部最小,那么mid > mid+1,mid ~ mid+1是局部下降的,N-2~N-1是局部上扬的,断言mid ~ N-1上必有局部最小;
代码如下:
查看代码
package com.cy.class03;
/**
* 局部最小值问题
*/
public class Code04_BSAwesome {
/**
* 找出局部最小值的下标位置
* arr整体无序,相邻的数不相等
* <p>
* 如果数组长度为1,直接返回这个数本身
*
* 原来写的是:while(L<=R), index = mid; return index;
* 这么写可能报indexOutOfBound错误,反例就是:[3,1,0]会报数据越界错误 ---> 应该 L < R
*
* 如果改成while(L<R),index = mid, return index也不行,一样报越界错误 ---- 应该 L < R - 1
* 反例:[3,2,3,2,3]
*
* 结合上面,L < R 和 L < R - 1,改成 L < R - 1
*/
public static int oneMinIndex(int[] arr) {
if (arr == null || arr.length == 0) {
return -1;
}
int N = arr.length;
if (N == 1) {
return 0;
}
if (arr[0] < arr[1]) {
return 0;
}
if (arr[N - 1] < arr[N - 2]) {
return N - 1;
}
int L = 0;
int R = N - 1;
while (L < R - 1) {
int mid = (L + R) / 2;
if (arr[mid] < arr[mid - 1] && arr[mid] < arr[mid + 1]) {
return mid;
} else if (arr[mid] > arr[mid - 1]) {
R = mid - 1;
} else { // arr[mid] > arr[mid + 1]
L = mid + 1;
}
}
return arr[L] < arr[R] ? L : R;
}
// 生成随机数组,且相邻数不相等
public static int[] randomArray(int maxLen, int maxValue) {
int len = (int) (Math.random() * maxLen);
int[] arr = new int[len];
if (len > 0) {
arr[0] = (int) (Math.random() * maxValue);
for (int i = 1; i < len; i++) {
do {
arr[i] = (int) (Math.random() * maxValue);
} while (arr[i] == arr[i - 1]);
}
}
return arr;
}
// 也用于测试
public static boolean check(int[] arr, int minIndex) {
if (arr.length == 0) {
return minIndex == -1;
}
int left = minIndex - 1;
int right = minIndex + 1;
boolean leftBigger = left >= 0 ? arr[left] > arr[minIndex] : true;
boolean rightBigger = right < arr.length ? arr[right] > arr[minIndex] : true;
return leftBigger && rightBigger;
}
public static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
public static void main(String[] args) {
int maxLen = 100;
int maxValue = 200;
int testTime = 1000000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int[] arr = randomArray(maxLen, maxValue);
int ans = oneMinIndex(arr);
if (!check(arr, ans)) {
printArray(arr);
System.out.println(ans);
break;
}
}
System.out.println("测试结束");
}
}所以,二分法不一定需要有序,例如上面的局部最小值问题。只要有一侧肯定有,那就可以使用二分。
--



 浙公网安备 33010602011771号
浙公网安备 33010602011771号