3.＜tag-二叉树和满二叉树, 完全二叉树, 平衡二叉树等树性质＞-lt.222. 完全二叉树的节点个数+lt.110. 平衡二叉树 (同剑指 Offer 55 - II. 平衡二叉树)

lt.222. 完全二叉树的节点个数

[案例需求]

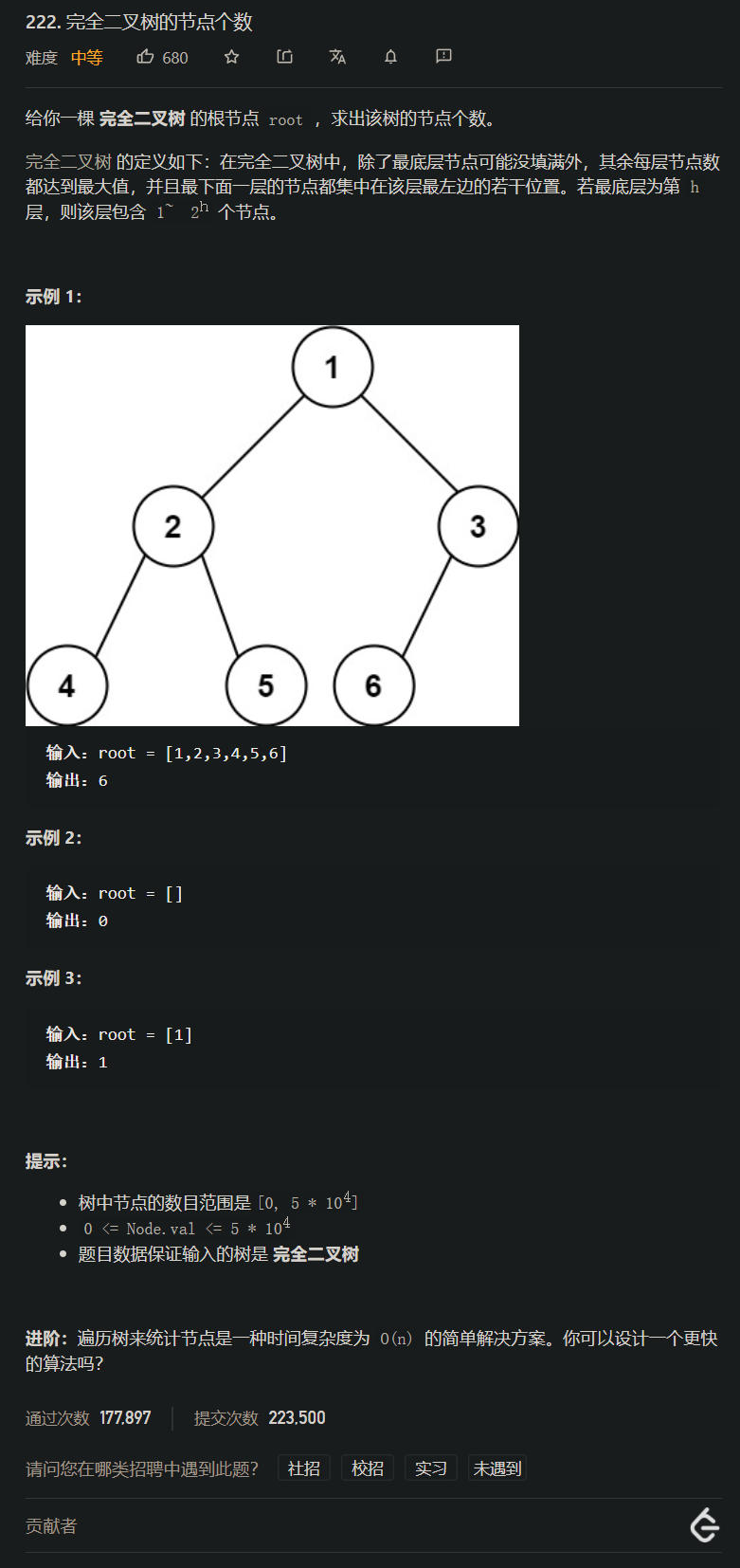
[思路分析一, (DFS)通用递归写法]

这道题目的递归法和求二叉树的深度写法类似， 而迭代法，二叉树：层序遍历的遍历模板 稍稍修改一下，记录遍历的节点数量就可以了。

递归遍历的顺序依然是后序（左右中）。

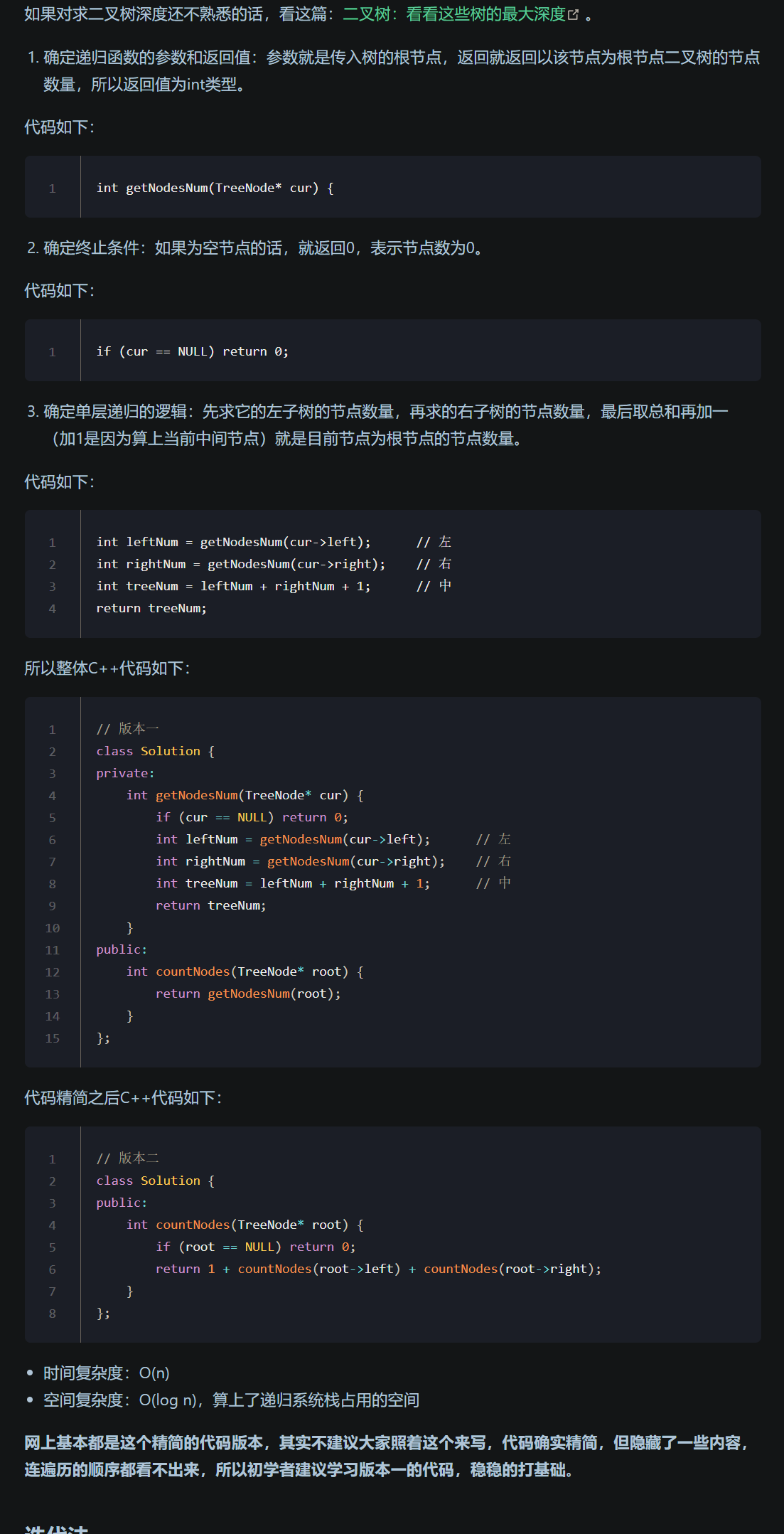
[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        //DFS
        // 递归出口
        if(root == null)return 0;

        //单层递归逻辑, 返回值
        int leftCount = countNodes(root.left);
        int rightCount = countNodes(root.right);   

        int count = leftCount + rightCount + 1;
        
        return count;
    }
}

[思路分析二, (BFS)层寻遍历写法]

[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        //层序遍历写法
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null)return 0;
        queue.add(root);

        int count = 0;
        while(!queue.isEmpty()){
            int size = queue.size();

            for(int i = 0; i < size; i++){
                root = queue.poll();
                count++;

                if(root.left != null)queue.add(root.left);
                if(root.right != null)queue.add(root.right);
            }
        }
        return count;
    }
}

[思路分析二, 针对完全二叉树性质的写法]

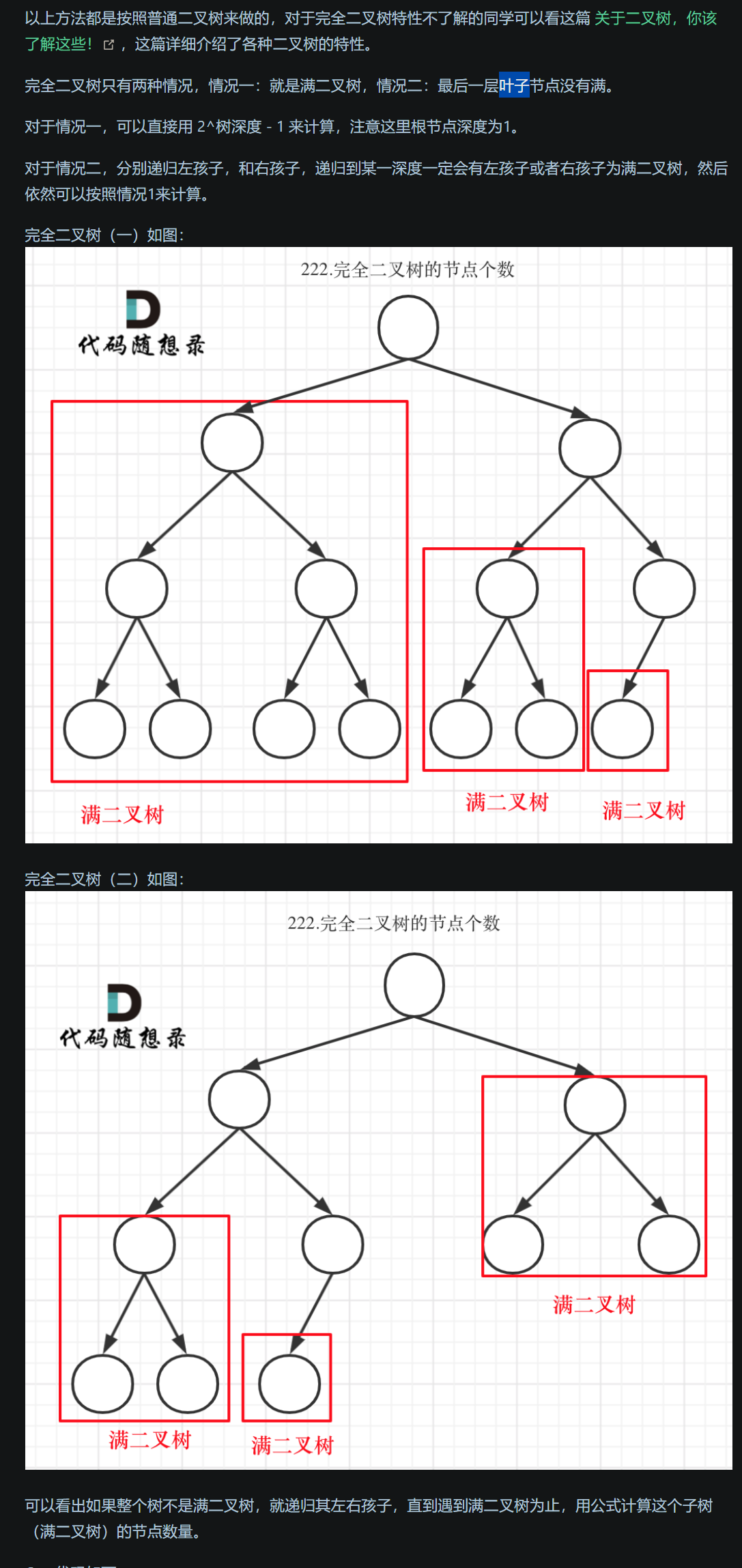
[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) == -1 ? false : true;
    }

    //求二叉树高度的方法
    // 递归参数和返回值, 参数: 当前节点(把它看做根节点),
    //返回值: 以当前节点为根节点的树的高度(不平衡时返回-1)
    private int getHeight(TreeNode root){
       //递归终止条件
       if(root == null)return 0;

       //单层递归逻辑
       //因为平衡二叉树是当前节点的左右子树的高度作比较
       //所以, 在单层递归逻辑中(我们可以把当前节点看作是一棵树的根节点, 
       //对于他的左右子树都要分别求出左子树的高度和右子树的高度, 
       //然后比较左右子树的高度之差, 如果大于1了则返回-1即可, 不大于1的话说明这个子树是平衡二叉树,
       // 我们把以当前节点为根节点的树的高度值直接返回)
       int leftHeight = getHeight(root.left);
       if(leftHeight == -1)return -1;

       int rightHeight = getHeight(root.right);
       if(rightHeight == -1)return -1;

       int result = 0;

       if(Math.abs(leftHeight - rightHeight) > 1){
           result = -1;
       }else{
           result = 1 + Math.max(leftHeight, rightHeight);
       }
       
       return result;
    }
}

lt.110. 平衡二叉树

[案例需求]

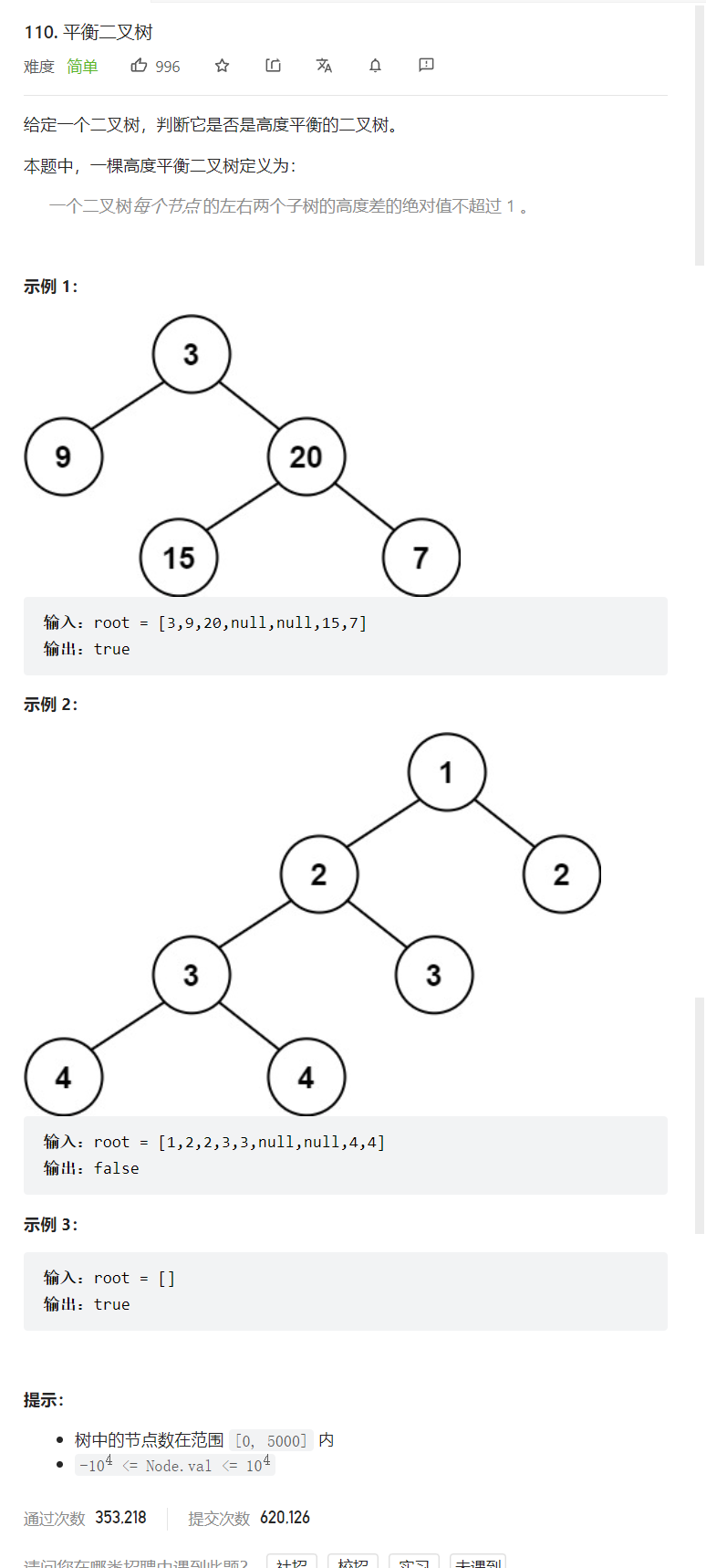
关于二叉树求高度和深度的区别

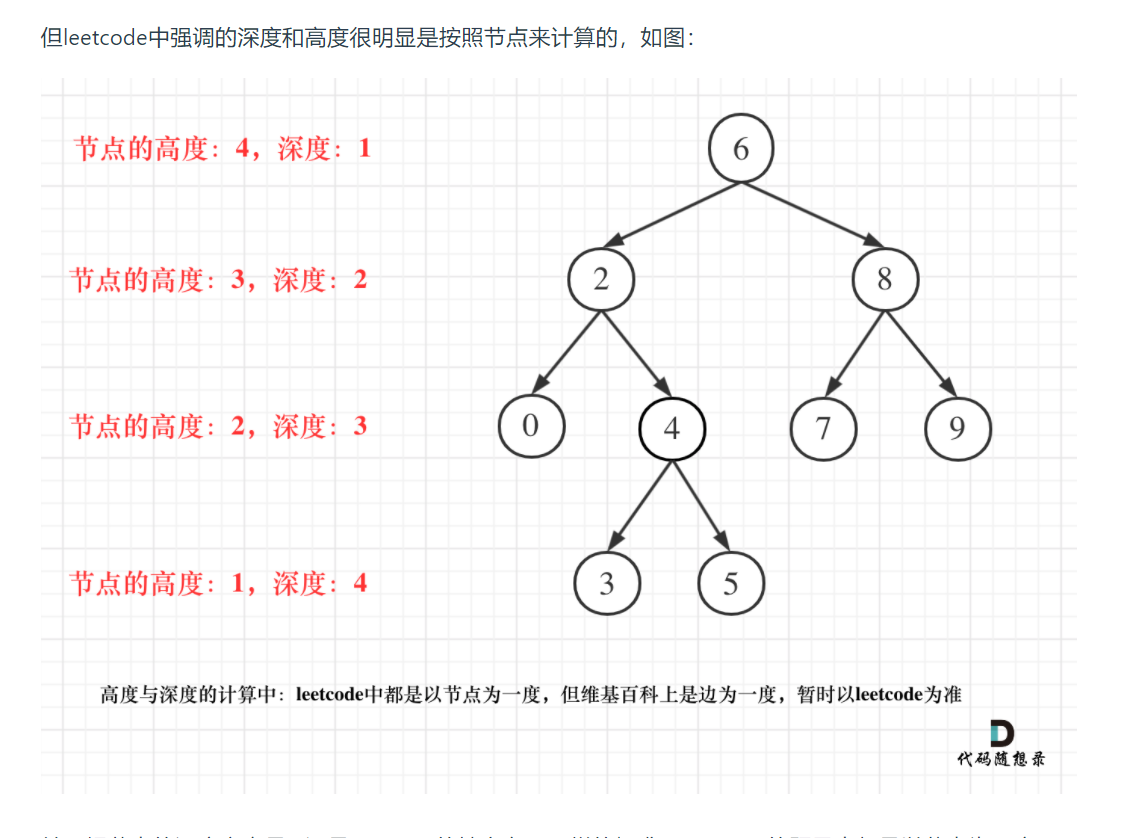
[思路分析一, 递归法]

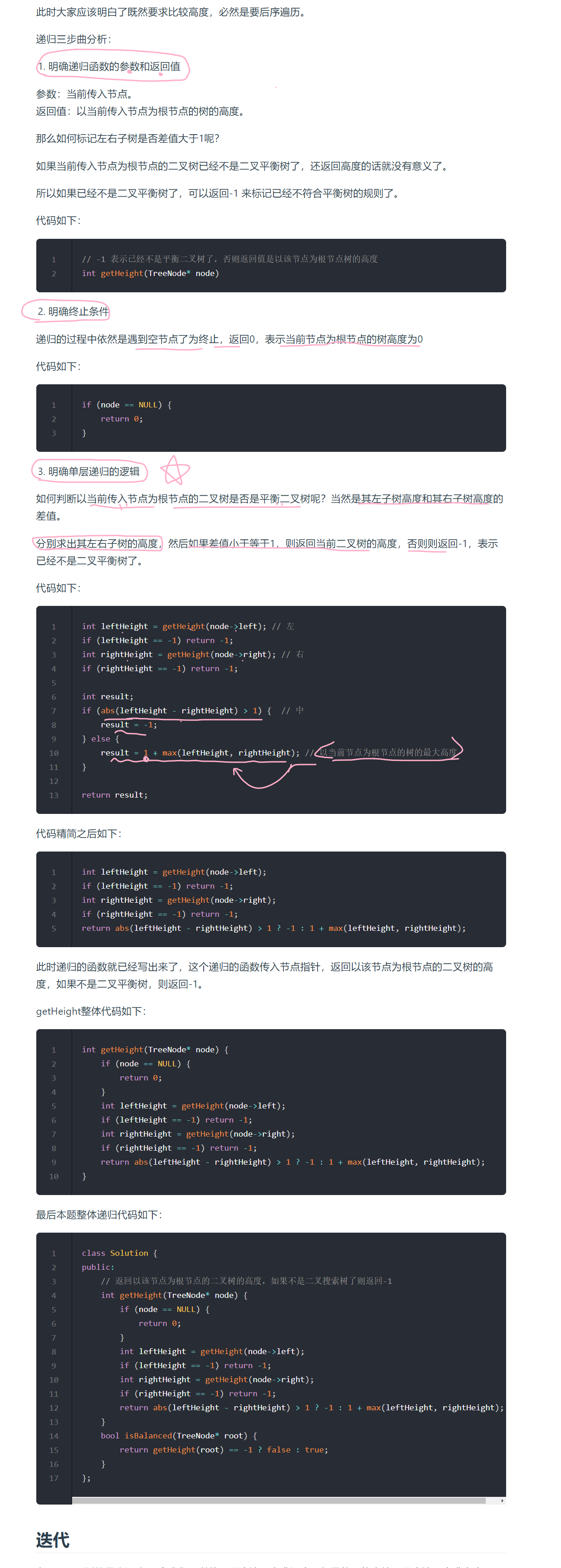
[代码实现]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) == -1 ? false : true;
    }

    //求二叉树高度的方法
    // 递归参数和返回值, 参数: 当前节点(把它看做根节点),
    //返回值: 以当前节点为根节点的数的高度(不平衡时返回-1)
    private int getHeight(TreeNode root){
       //递归终止条件
       if(root == null)return 0;

       //单层递归逻辑
       int leftHeight = getHeight(root.left);
       if(leftHeight == -1)return -1;

       int rightHeight = getHeight(root.right);
       if(rightHeight == -1)return -1;

       int result = 0;

       if(Math.abs(leftHeight - rightHeight) > 1){
           result = -1;
       }else{
           result = 1 + Math.max(leftHeight, rightHeight);
       }
       
       return result;
    }
}

[思路分析二, 迭代法]

• 待补充

[代码实现]