25-0817 MATLAB中 fft 与 pwelch 关系

1.fft与pwelch的概念差别

首先要明确：fft 用来做频谱，pwelch 用来做功率谱。这里的重点是说明二者的联系。参考CSDN博客 https://blog.csdn.net/zhanghaijun2013/article/details/106038488

• fft：利用快速傅里叶变换（Fast Fourier Transform, FFT）来计算离散傅里叶变换（Discrete Fourier Transform, DFT）；
• pwelch：求功率谱，常用如下的函数

pxx = pwelch(x,window,noverlap,nfft)
[pxx,f] = pwelch(x,window,noverlap,f,fs)

 

welch的计算过程大致如下：

1. 分段（Segmenting）：将信号分割成若干段，每段长度等于 window 的长度；

2. 加窗（Windowing）：对每段信号乘以指定的窗函数，例如矩形窗、汉明窗等；

3. FFT 计算：对每段加窗后的信号做 FFT，FFT 点数为 nfft，得到该段的周期图（Periodogram，即功率谱）；分段之间允许重叠 noverlap 个采样点；

4. 平均（Averaging）：将所有分段得到的周期图取平均，得到最终的功率谱密度（PSD）估计；f 对应的是 Pxx 的频率点。

2.通过代码对比fft与pwelch

具体对比代码如下：

 

close all; clear; clc;

%% 参数设置
fs = 160;       % 采样频率 (Hz)
N  =40;        % 信号长度
t  = ((0:N-1)/fs).'; % 时间向量（列向量）
f0 = 20;        % 信号频率 (Hz)

%% 信号
x = cos(2*pi*f0*t);   % 单频余弦信号（列向量）

%% FFT 单段 Periodogram
X = fft(x);                        % 计算 FFT（频域表示）
N_oneside = floor(N/2) + 1;           % 单边谱点数（奇偶统一写法）
psdx = abs(X(1:N_oneside)).^2/(fs*N); % 功率谱密度：|X(k)|^2 / (fs * N)

%% 能量翻倍规则（奇偶性区别）
% FFT 得到的是双边谱，为了转成单边谱需要修正能量：
% - 对于直流分量 (0 Hz) 和 Nyquist 频点（仅偶数 N 时存在），不需要翻倍；
% - 其他频率分量需要翻倍，以补偿被截掉的负频率部分。
if mod(N,2) == 0      % 偶数 N：存在 Nyquist 点
    psdx(2:end - 1) = 2*psdx(2:end - 1);  % 能量翻倍，除 DC 和 Nyquist 点
else                  % 奇数 N：没有 Nyquist 点
    psdx(2:end)   = 2*psdx(2:end);    % 能量翻倍，除 DC 点
end

%% 频率轴
freq = (0:N_oneside-1)'*(fs/N);   % 对应 psdx 的频率坐标（列向量）

%% Welch 方法（单段，矩形窗，无重叠）
% pwelch 实质上是对信号分段加窗 -> FFT -> 求周期图 -> 取平均
% 在这里设置为单段、矩形窗，结果与 FFT Periodogram 理论上应一致
[pxx,f] = pwelch(x, rectwin(N), 0, N, fs, 'onesided');

%% 线性尺度对比
figure;
plot(freq, psdx, 'r', 'LineWidth', 1.2, 'DisplayName','FFT-Periodogram'); hold on;
plot(f, pxx, 'b--', 'LineWidth', 1.2, 'DisplayName','Welch (Rect, 1 seg)');
xlabel('Frequency (Hz)'); ylabel('PSD (Power/Hz)');
title('功率谱密度对比（线性）');
legend; grid on;

%% dB 尺度对比
figure;
plot(freq, 10*log10(psdx), 'r', 'LineWidth', 1.2, 'DisplayName','FFT-Periodogram'); hold on;
plot(f, 10*log10(pxx), 'b--', 'LineWidth', 1.2, 'DisplayName','Welch (Rect, 1 seg)');
xlabel('Frequency (Hz)'); ylabel('PSD (dB/Hz)');
title('功率谱密度对比（dB）');
legend; grid on;

　　

运行结果如下

 

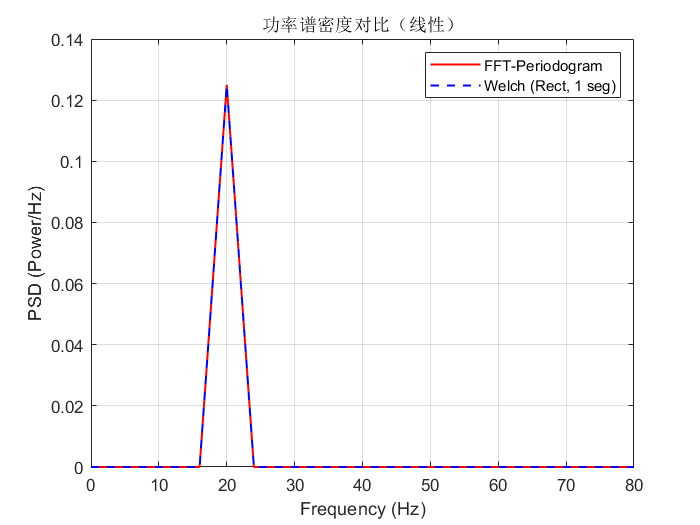
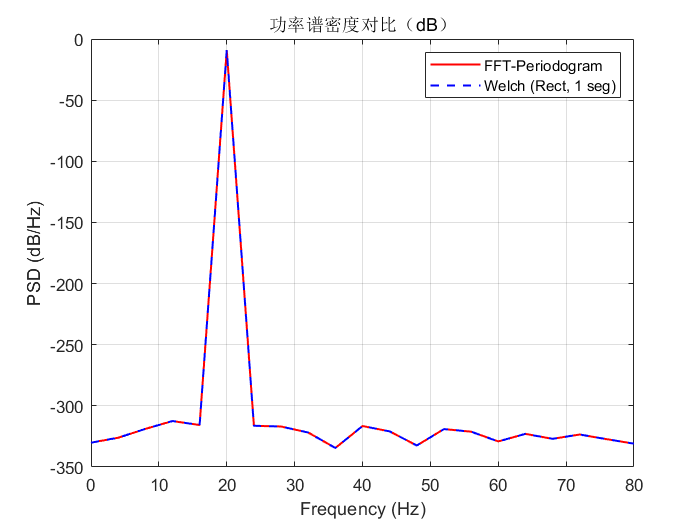
关键点说明

特别需要注意下面几行代码：

if mod(N,2) == 0      % 偶数 N：存在 Nyquist 点
    psdx(2:end-1) = 2*psdx(2:end-1);  % 能量翻倍，除 DC 和 Nyquist 点
else                  % 奇数 N：没有 Nyquist 点
    psdx(2:end)   = 2*psdx(2:end);    % 能量翻倍，除 DC 点
end

FFT 的结果本质上是双边谱，为了得到单边谱，需要进行能量修正：砍掉了一半的频率成分，就必须把非重叠部分的能量乘 2。

对于 nfft = N，第 k 个频率点索引为 f_k = k / N * fs, k = 0, 1, ... , N - 1，单边谱点数为 N_oneside = floor(N/2) + 1，分两种情况讨论：

当 N 为奇数时，最大正频率为 k = (N - 1) / 2，即 f_k = (N - 1) / (2N) *fs < fs / 2，故重叠部分为 0 Hz 点  

当 N 为偶数时，最大正频率为 k = N / 2，即 f_k = fs / 2，故重叠部分为 0 Hz 点 ( DC ) 和Nyquist 频率点。

在当忽略这一点时，会对单边谱最后一个频率点产生误差

例如下图当 N 为偶数时，误将除了 0Hz 以外的点都进行能量翻倍的结果，可以看到末尾频点能量高了 10*log10(2) ≈ 3 dB。

 

 

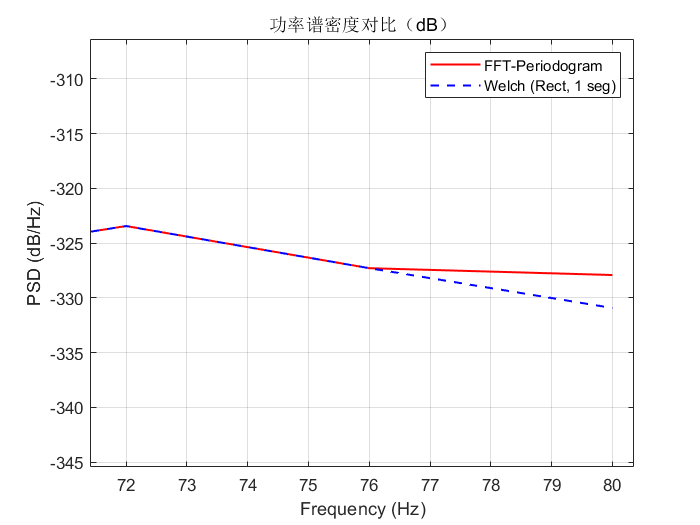
另外注意代码中 freq 和 f 是转置关系，对应 psdx 和 pxx 也是转置关系，因为 pwelch 函数生成的数据为列向量。

3.加窗后对比

最后，我们将代码中矩形窗改为汉宁窗（因为更常用，来减少频谱泄露效应），对比两种窗函数得到的功率谱，代码可以直接复制到前面代码末尾运行。

 

%% ===============================
%  使用 Hann 窗 + 能量补偿
% ===============================
w = hann(N);                    % Hann 窗
xw = x .* w;                    % 加窗信号（列向量）
U = sum(w.^2)/N;                % 窗函数能量修正因子

% FFT-Periodogram with Hann
Xw = fft(xw);
psdx_hann = abs(Xw(1:N_oneside)).^2/(fs*N*U);

% 能量翻倍规则（同上）
if mod(N,2) == 0
    psdx_hann(2:end-1) = 2*psdx_hann(2:end-1);
else
    psdx_hann(2:end) = 2*psdx_hann(2:end);
end

freq = (0:N_oneside-1)*(fs/N);   % 频率轴

% Welch 方法（Hann 窗, 单段, 无重叠）
[pxx_hann,f_hann] = pwelch(x, hann(N), 0, N, fs, 'onesided');

%% 线性尺度对比 (Hann)
figure;
plot(freq, psdx_hann, 'r', 'LineWidth', 1.2, 'DisplayName','FFT-Periodogram (Hann+comp)'); hold on;
plot(f_hann, pxx_hann, 'b--', 'LineWidth', 1.2, 'DisplayName','Welch (Hann, 1 seg)');
xlabel('Frequency (Hz)'); ylabel('PSD (Power/Hz)');
title('功率谱密度对比（Hann 窗, 线性）');
legend; grid on;

%% dB 尺度对比 (Hann)
figure;
plot(freq, 10*log10(psdx_hann), 'r', 'LineWidth', 1.2, 'DisplayName','FFT-Periodogram (Hann+comp)'); hold on;
plot(f_hann, 10*log10(pxx_hann), 'b--', 'LineWidth', 1.2, 'DisplayName','Welch (Hann, 1 seg)');
xlabel('Frequency (Hz)'); ylabel('PSD (dB/Hz)');
title('功率谱密度对比（Hann 窗, dB）');
legend; grid on;

 

　　

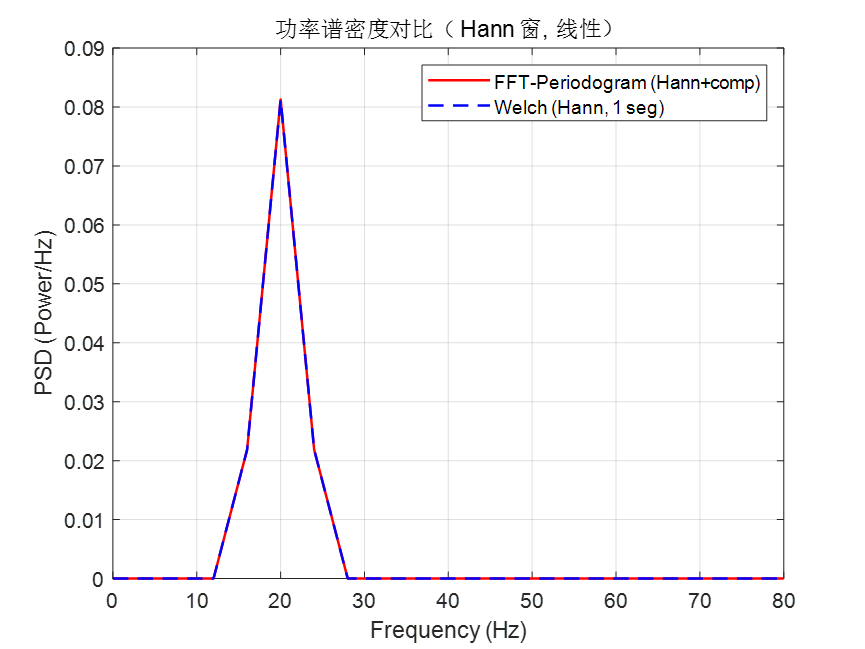
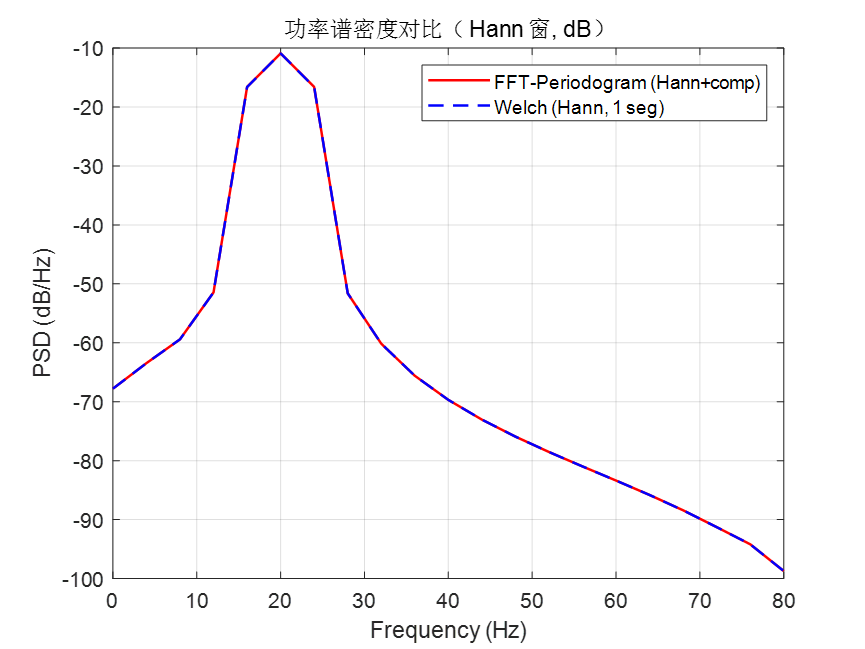
对比后，我们看到加窗后频谱反而泄露了，这个原因是因为在 f0 = 20 这个频率点正好不会产生频谱泄露，加窗反而会影响干净的频谱。具体可以参照我的另外一篇博客：https://www.cnblogs.com/scut4787749233/p/19064604

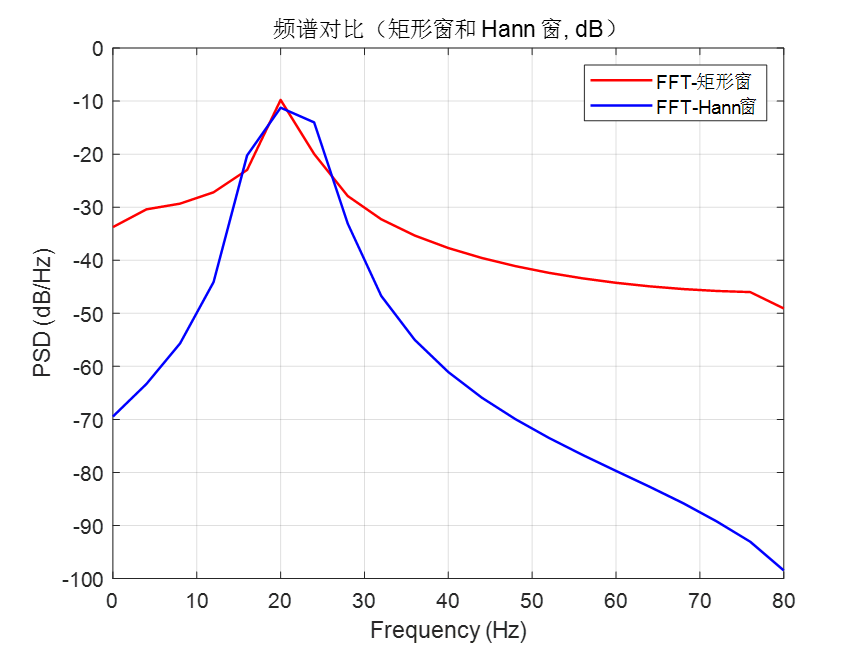
若把 f0 改为 21，我们对比一下FFT能量翻倍后，矩形窗和Hann窗的结果（代码略），可以看到加上Hann窗后明显抑制了频谱泄露