算法第五章实验课作业

1.题目描述

7-2 最小重量机器设计问题 (25 分)

设某一机器由n个部件组成，每一种部件都可以从m个不同的供应商处购得。设\(w_{ij}\)是从供应商j 处购得的部件i的重量,\(c_{ij}\)是相应的价格。 试设计一个算法，给出总价格不超过d的最小重量机器设计。

输入格式:

第一行有3 个正整数n ，m和d， 0<n<30, 0<m<30, 接下来的2n 行，每行n个数。前n行是c，后n行是w。

输出格式:

输出计算出的最小重量，以及每个部件的供应商

输入样例:

3 3 4
1 2 3
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
结尾无空行

输出样例:

在这里给出相应的输出。例如：
4
1 3 1

算法描述

解空间

设有n个物品，m个供应商
\(\{(i_1,i_2,...,i_n)|\forall i=1,...,m\}\)

解空间树

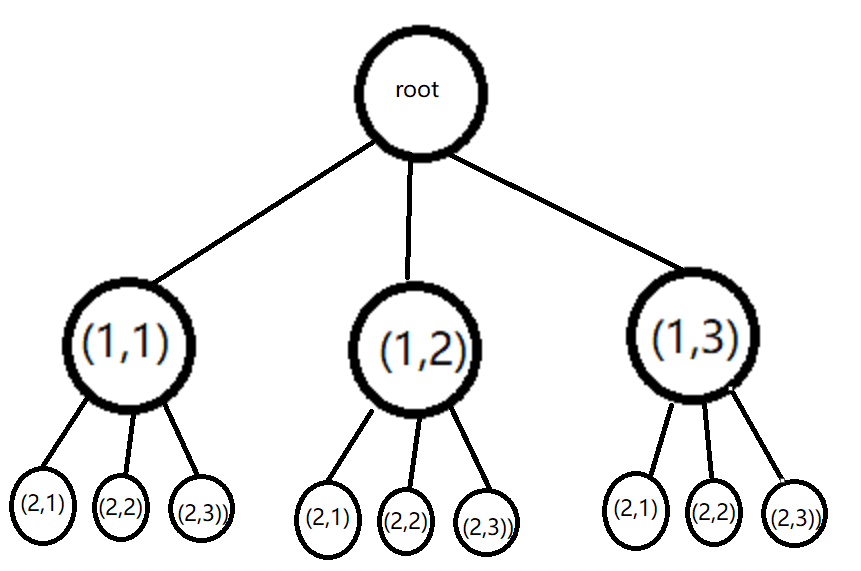
结点状态

当遍历到第一层结点时，遍历公司数，建立数组x[n],把当前公司的编号赋值给x[1],然后进行第二件物品的公司遍历，把公司编号赋给x[2],以此类推。当把物品遍历完之后，再回到第一件物品重新选择不同公司。

算法实现

#include<bits/stdc++.h>
using namespace std;
int n,m,d;
int w[100][100];
int c[100][100];
int x[100];
int currc[100];
int result[100];
int minx=INT_MAX;
int cp;
int cw;
// bool bound(int t){
// 	int mon=0;
// 	for(int i=1;i<=t;i++){
// 		mon+=c[i][x[i]];
// 		if(mon>d||(mon==d&&t<n)){
// 			return false;
// 		}
// 	}	
// 	return true;
// }
// bool constrant(int t){
// 	int mon=0;
// 	for(int i=1;i<=t;i++){
// 		mon+=w[i][x[i]];
// 		if(mon>=minx){
// 			return false;
// 		}
// 	}
// 	return true;
// }
void backtrack(int t){
	if(t>n){
		if(cw<minx){
			minx=cw;
			for(int i=1;i<t;i++){
				result[i]=x[i];
			}
		}
//		int sum=0;
//		for(int i=1;i<t;i++){
//			sum+=w[i][x[i]];
//		}
//		if(sum<minx){
//			minx=sum;
//			
//		}
		return ;
	}
	for(int i=1;i<=m;i++){
		cp+=c[t][i];
		cw+=w[t][i];
		x[t]=i;
		if(cp<=d&&cw<minx){
			backtrack(t+1);
		}
		cp-=c[t][i];
		cw-=w[t][i];
	}
}
int main(){
	cin>>n>>m>>d;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>w[i][j];
		}
	}
//	for(int i=1;i<=n;i++){
//		sort(w[i]+1,w[i]+m+1);
//	}
//	for(int i=1;i<=n;i++){
//		for(int j=1;j<=m;j++){
//			cout<<w[i][j];
//		}
//		cout<<endl;
//	}
	backtrack(1);
	cout<<minx<<endl;
	for(int i=1;i<=n;i++){
		cout<<result[i]<<" ";
	}
	return 0;
}

本题需要剪枝。

我对回溯的理解

回溯的解空间树有两种类型：一是子集树，二是排列数。子集树类似背包问题，排列树类似旅行商问题。回溯要求把所有情况遍历出来，因此时间复杂度很高。但是相对于动态规划更容易想到。