2025.9 做题记录

CF2133F

设第 \(i\) 个 creeper 的爆炸范围是 \([l_i,r_i]\)。

题目转化为选择最少的线段覆盖 \([1,n]\)。

但是只有活着的 creeper 可以引爆，所以还有一个条件是 \(\nexists i,j\) 满足 \(r_i \ge j \land l_j \le i\)。如果这两个条件满足其一只需要调剂一下（换个引爆顺序）就可以了。于是dp。

设 \(dp_{i,j}\) 表示杀了前 \(i\) 只 creeper，引爆的最右端的 creeper 是 \(j\)（为了不让 \(j\) 跟后面的矛盾）。容易发现只有 \(r_j=i\) 的情况是有前途的（否则不引爆 \(j\) 一定更优）。所以状态改为 \(dp_i\) 表示已经杀了前 \(r_i\) 只 creeper，引爆了第 \(i\) 只的最小操作数。

把所有 creeper 按 \(r_i\) 排序 dp。

按此排序理由：

如果直接按照原顺序 dp，可能会出现后引爆的 \(r_i<\) 先引爆的 \(r_j\)。这样的问题在于，后面的 dp 会考虑不到被 \(j\) 炸的部分情况导致某些 creeper 在引爆之前已经被炸死的情况。

剩下的部分似乎是套路的。

整理式子得到：

\[l_i-1 \le r_j < i \qquad(1) \]

\[j<l_i \le r_j+1 \qquad (2) \]

这两者任满足其一就可以用 \(j\) 向 \(i\) 转移。

\((1)\) 可以用 \(dp_j\) 更新 \(r_j\) ，查询 \([l_i-1,i)\) 的最小值。

\((2)\) 可以用 \(dp_j\) 更新 \((j,r_j+1]\)，单点查询 \(l_i\)。

线段树维护两个操作是容易的。输出方案只需要记录转移点（答案来源），建图跑拓扑就可以了。

于是最终做到 \(O(n\log n)\)。

submission。

P5203 [USACO19JAN] Exercise Route P

容易发现两条非树边能组成环当且仅当它们两点在树上的路径有交。

证明：

首先若它们的路径无交，显然无法连通。

否则将它们路径的交断掉，再加上这两条边即可。

于是问题转化为求给出的边中，有多少对边在树上的路径上两两有交。

把边 \((u,v)\) 拆成 \((an,u)\) 和 \((an,v)\) （\(an\) 为 \(lca(u,v)\)），这样每条边都是直上直下的。

可以使用类似于差分的想法，把每一条路径 \(an\) 往下的点都 \(+1\)，统计时 \(val_u+val_v-2val_{an}\) 就是与起点（以 \(an\) 为起点的第一条边，而不是点）是这条边或在这条边之下，与这条边有交的边数。

但是你发现有情况算重了。

• 两条边共用了中间的一段，于是相交被统计了两遍。

sol：

设 \(pub[(x,y)]\) 为共用 \((x,an),(y,an)\) 这一段的边数，相当于这部分的贡献算了两倍，我们希望统计 \(\binom{pub}{2}\) 次答案，实际上却统计了 \(2\binom{pub}{2}\) 的答案，减去即可。

• 起点共用，于是这些边各把对方统计到了答案中。

sol：

设 \(cnt_e\) 为这条边作为起点的次数，我们希望统计 \(\binom{cnt}{2}\) 次，实际却统计了 \(cnt^2\) 次，同样减去多算的即可。

实现比较套路，用边下方的点代表边，按上述过程模拟即可。

复杂度 \(O(n\log n)\)。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pii pair<int,int>
#define mkp make_pair
const int maxn=200004;
int n,m;
int a[maxn],b[maxn],an[maxn];
struct Edge{int to,nxt;}edg[maxn<<1];
int hd[maxn],tt;
inline void add(int u,int v){edg[++tt]={v,hd[u]};hd[u]=tt;}
namespace Treediv{
	int dep[maxn],f[maxn],siz[maxn],son[maxn];
	void dfs0(int u,int fa){
		dep[u]=dep[fa]+1,f[u]=fa,siz[u]=1;
		for(int e=hd[u],v;e;e=edg[e].nxt){
			v=edg[e].to;if(v==fa)continue;
			dfs0(v,u);
			siz[u]+=siz[v];(siz[v]>siz[son[u]])&&(son[u]=v);
		}
	}
	int tp[maxn];
	void dfs1(int u,int tpu){
		tp[u]=tpu;
		if(!son[u]) return;
		dfs1(son[u],tpu);
		for(int e=hd[u],v;e;e=edg[e].nxt){
			v=edg[e].to;if(v==f[u]||v==son[u])continue;
			dfs1(v,v);
		}
	}
	inline int lca(int x,int y){
		while(tp[x]^tp[y]){
			if(dep[tp[x]]<dep[tp[y]]) swap(x,y);
			x=f[tp[x]];
		}
		return (dep[x]>dep[y]?y:x);
	}
	inline int fd(int x,int u){//找边起点
		if(x==u) return 0;
		while(dep[tp[x]]>dep[u]+1) x=f[tp[x]];
		return (tp[x]==tp[u]?son[u]:tp[x]);
	}
}using namespace Treediv;
int tag[maxn];
map <pii,int> pub;
int res[maxn];
void dfs(int u,int cur){
	res[u]=cur;
	for(int e=hd[u],v;e;e=edg[e].nxt){
		v=edg[e].to;if(v==f[u])continue;
		dfs(v,cur+tag[v]);
	}
}
inline ll calc(int x){return 1ll*x*(x-1)/2;}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>a[i]>>b[i];
	for(int i=1;i<n;i++) add(a[i],b[i]),add(b[i],a[i]);
	dfs0(1,0);dfs1(1,1);
	for(int i=n;i<=m;i++){
		an[i]=lca(a[i],b[i]);
		int bx=fd(a[i],an[i]),by=fd(b[i],an[i]);
		if(bx>by)swap(bx,by),swap(a[i],b[i]);
		tag[bx]++,tag[by]++;
		if(bx&&by){pub[mkp(bx,by)]++;}
	}
	ll ans=0;
	dfs(1,0);
	for(int i=n;i<=m;i++)
		ans+=res[a[i]]+res[b[i]]-(res[an[i]]<<1);
	for(auto it=pub.begin();it!=pub.end();it++) ans-=calc(it->second);
	for(int i=2;i<=n;i++) ans-=1ll*tag[i]*tag[i]-calc(tag[i]);
	cout<<ans<<'\n';
	return 0;
}

CF516D Drazil and Morning Exercise

以树的中心为根，容易发现此时 \(f_u\ge f_{fa}\)。

证明：

当 \(u\) 在路径 \(S,T\) 上时，显然 \(u\) 一定会离中心方向的起点更远。

否则此时的 \(fa\) 一定离 \((S,T)\) 更近，所以 \(dis(S,u)\ge dis(S,fa) \wedge dis(T,u)\ge dis(T,fa)\)。

于是我们在每个点往上倍增找到能跟它分在一组的最高祖先，树上差分即可。复杂度 \(O(qn\log n)\)。

Submission。

CF526F Pudding Monsters

由于每行/每列只有一个棋子，所以条件转化为对于 \(k\) 个棋子， \(\max x-\min x+1=\max y-\min y+1=k\)。

考虑以 \(x\) 为下标同时满足长度和 \(x\) 的要求消掉一维，条件变为：\(r-l+1=\max y-\min y +1\)。

移项得：\(\max y-\min y-r+l=0\)。

考虑对 \(r\) 扫描线，动态维护满足条件的 \(l\) 个数。

但是恰好等于 \(0\) 不太好维护，注意到 \(\max y-\min y-r+l\ge 0\)，于是转而维护最小值和最小值个数。

使用线段树，线段树区间 \([L,R]\) 表示 \(l\in [L,r]\) 时当前 \(r\) 有多少个答案。

考虑四项分别怎么维护。

• \(+l\)：此项是固定项，初始化时加上即可。
• \(-r\)：在 \(r\) 向后移时减小，因此每次扫时全局 \(-1\)。
• \(\max y\)：使用一个单调栈，当前值大于栈顶元素时更新原来栈顶元素支配的那一段并弹栈。
• \(\min y\)：同上。

于是做完。

更新部分代码：

M.upd(1,1,n,-1);
while(tx&&a[stx[tx]]<=a[r]){M.upd(1,stx[tx-1]+1,stx[tx],a[r]-a[stx[tx]]);tx--;}
while(tn&&a[stn[tn]]>=a[r]){M.upd(1,stn[tn-1]+1,stn[tn],a[stn[tn]]-a[r]);tn--;}
stx[++tx]=r,stn[++tn]=r;

按理来说最大/最小值应该要更新到当前位置，但极其巧妙的是，上一个栈顶元素一定是 \(r-1\) 所以 \([1,r-1]\) 一定会被更新到，同时区间 \([r,r]\) 的最大/最小值一定是 \(a_r\)，加不加没什么影响。

P3783 [SDOI2017] 天才黑客 - 洛谷

厉害题。。

description

有 \(n\) 个点，\(m\) 条单向边，每条边形如 \((u,v,w,d)\)，其中 \(d\) 是一个字符串，代表通过这条边需要花费 \(w\)。假设上一条通过的边是 \((a,b,c,d')\)，那么通过这条边时有额外 \(\operatorname{LCP}(d,d')\)（\(\operatorname{LCP}\) 即最长公共子序列）的代价。求单源最短路。

solution

\(\operatorname{LCP}\) 可以转化为字符串在字典树上对应节点的 \(\operatorname{LCA}\)。

花费完全跟点没什么关系说明可以点边互换，即每个点的入边向出边两两连边。

对于原边权，我们可以把一条边拆成一个入点一个出点，入点只有入边，出点只有出边，对于原来的一条边，它的入点向它的出点连边权为 \(w\) 的边。

最后答案取每个点所有入边出点的最短路最小值即可。

这样的点数是 \(O(m)\) 的，但新边数量是 \(O(m^2)\) 的。

有一个结论：

设有一个节点序列 \(a_1,a_2,\cdots,a_n\)，我们将其按照 dfn 序从小到大排序，得到 \(b_1,b_2,\cdots,b_n\)。

那么 \(dep_{ \operatorname{LCA}(b_i,b_j)}=\max_{k=i}^{k<j}dep_{ \operatorname{LCA}(b_k,b_{k+1})}\)。

那么考虑对于一个原图上的点 \(u\)，把它的所有边按 \(d\) 在树上的 dfn 序排序，将 \(u\) 前缀 \([1,i]\) 中所有的入边向后缀 \([i+1,n]\) 中的所有出边连长度为 \(dep_{ \operatorname{LCA}(b_i,b_{i+1})}\) 的边。按照上面的结论，此时 \(i\) 到 \(j\) 最短的那条边就是我们原来需要的边。而由于我们跑的是最短路，其余多加的边没有影响。

使用前后缀优化建图，边数即可优化成 \(O(m)\) 级别的，可以通过。

稍微具体来说，新建前缀入边，前缀出边，后缀入边，后缀出边的虚点，按上述规则将代表入边的虚点和代表出边的虚点一一连接即可。

复杂度 \(O(Tm\log m)\)。

code

submission。

P6118 [JOI 2019 Final] 独特的城市 / Unique Cities

感觉是可以见见思路的奇怪题。

容易发现对于一个城市来说独特的城市一定在这个点到距离这个点最远的点的路径上。而根据经典结论，这个最远的点必然是直径两端点之一。

于是我们分别从两端点搜索，那么一个点独特的城市一定是它的祖先，方便处理。

这里可以浅浅猜测这是个数据结构不好维护的东西。

发现可以对 \(u\) 做出贡献（让独特城市对于 \(u\) 来说不再独特） 只有两种可能：

• 在 \(u\) 子树内
• 在 \(u\) 的某个祖先 \(anc\) 的子树内

第二种情况可以在 \(fa\) 进去搜索时直接维护（对于这两个来说距离各 \(+1\) 所以原影响不变），只需考虑如何维护第一种。

第一种情况即 \(u\) 最深的子树。但是考虑如果在这里把这个贡献算上，递归进最深子树的时候就得重新加回来一些点（因为少了最深子树的贡献），这样复杂度就不对了。

于是再记录 \(u\) 第二深的子树深度，先把第二深的子树贡献部分删掉，递归进长儿子。再计算长儿子子树的贡献，此时维护集合就是 \(u\) 的独特城市。再递归进 \(u\) 的非长儿子计算即可。

每次递归到一个点时记得加入/删除它的父亲。

维护答案部分类似莫队，比较简单。

submission。

P4137 Rmq Problem / mex

description

给你一个长度为 \(n\) 的序列，有 \(m\) 次询问，每次回答 \([l,r]\) 的 \(\operatorname{mex}\)。\(n,m\le 2\times 10^5\)。

solution

记一个非常喵的做法^^。

考虑可持久化权值线段树维护 \(val\) 最后一次出现位置的区间最小值 \(mn\)。

那么对于一个询问 \([l,r]\)，答案就是 \(rt_r\) 中最前的 \(mn<l\) 的位置。简单线段树上二分即可。

同时注意到 \(\operatorname{mex}<n\)，所以只用记录 \(<n\) 的数，离散化都省了。

代码随便写，复杂度 \(O(n\log n)\)。

link。

CF2131F Unjust Binary Life

妈的，赛时犯唐了这都做不出来。

solution

可以转化一下：只有 \(a_i=b_j\) 时 \((i,j)\) 是合法的格子。因为 \((i,j)\) 一次只能移动一个，下一轮的 \(a_i'\) 和 \(b_j'\) 有一个和上一轮相同，又有 \(a_i'=b_j'\)，所以当前移动到的新的格子还是满足 \(a_i=b_j=a_i'=b_j'\)，于是 \((1,1)\) 可以向右下走到 \((i,j)\) 的时候必然有 \(a_{1\sim i}\) 和 \(b_{1\sim j}\) 都相等。

设 \(sa\) 为 \(a\) 的前缀和，\(sb\) 为 \(b\) 的前缀和。

分类一下修改为全 \(1\) 或全 \(0\) 的情况，那么：\(f(i,j)=min(i+j-sa_i-sb_j,sa_i+sb_j)\)。

用经典结论较小值转绝对值：\(min(x,y)=\dfrac{x+y+|x-y|}{2}\)。

整理一下式子得到：\(f(i,j)=\dfrac{i+j-|(2sa_i-i)+(2sb_j-j)|}{2}\)。

\(\dfrac{i+j}{2}\) 随便求和算一下。对于后面的一项，将 \((2sa_i-i)\) 以值域为下标记录前缀的个数 \(cnt\) 和总和 \(sum\)。

扫一遍 \(j\)，设 \(cur=2sb_j-j\)，拆开绝对值得到：\(\sum_{i=1}^{n}|(2sa_i-i)+(2sb_j-j)|=(2n-cnt_{-cur})cur+sum_{2n}-sum_{-cur}\)。

复杂度 \(O(n)\)。

submission。

P9527 洒水器

疑似有点太人类智慧导致好长时间学不懂 / ll。

不能暴力做，发现 \(d\le 40\)，考虑在祖先上打标记。\(tag_{u,i}\) 表示在 \(u\) 的子树中和 \(u\) 的距离 \(\le i\) 的 \(v\) 的 \(tag\)。查询时暴力找 \(d\) 级祖先即可。

此时修改和查询均是 \(O(d)\) 的。

此时有一些点会被多次标记，如下图：

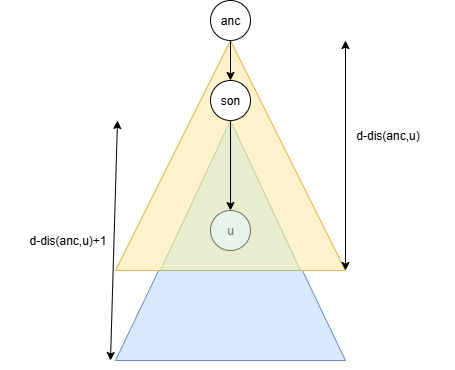
\(u\) 是当前点，\(anc\) 是 \(u\) 的一个祖先，\(u\) 在 \(anc\) 的儿子 \(son\) 的子树中。当 \(tag_{son,d-dis(son,u)},tag_{anc,d-dis(anc,u)}\) 分别覆盖（蓝色和黄色三角形）一次时，中间的绿色三角形那一块明显被多覆盖了一次。而这块三角形表示出来就是 \(tag_{son,d-dis(anc,u)-1}\) 即 \(tag_{son,d-dis(son,u)-2}\)。那我们每次只要在形如这样的位置上除以 \(w\) 就可以了。

问题是不保证模数有逆元。

观察到对于 \(son\) 来说，只有两个更新：\(tag_{son,d-dis(son,u)}\times w,tag_{son,d-dis(son,u)-2}\div w\)。于是相当于 \(tag_{son,d-dis(son,u)-2}\) 这一块没有操作，\(son\) 的第 \(d-dis(son,u),d-dis(son,u)-1\) 级后代 \(\times w\)。

于是更改 \(tag_{u,i}\) 的定义为 \(u\) 子树内距离 \(u\) 恰好为 \(i\) 的 \(tag\)。对于每个位置只用更新两个位置，所以修改还是 \(O(d)\) 的。

非常优雅地做完了。

submission。

33OJ #LK0005. GCD

description

给你一个 \(n\) 个数的正整数序列 \(a_1,a_2,\cdots,a_n\)。你需要把它们其中一些选入两组，满足：

• 这两组选的元素没有交。
• 第一组数的最大公约数乘以第一组的数字个数加上第二组数的最大公约数乘以第二组的数字个数之和最大。

solution

预处理 \(cnt_i\) 表示在序列中 \(i\) 的倍数有几个。

简单的暴力做法是对于每个 \(i\)，枚举比它大的 \(j\)：\(ans \gets (cnt_i-cnt_{\operatorname{lcm(i,j)}}) i+cnt_j j\)。原因是若有一个数同时是 \(i,j\) 的倍数，将它分进 \(j\) 的组答案更大。

考虑 \(\operatorname{lcm(i,j)}> V\) 时就没有影响了，所以我们把 \(\operatorname{lcm(i,j)}>V\) 和 \(\operatorname{lcm(i,j)}\le V\) 分开考虑。

• \(\operatorname{lcm(i,j)}> V\)：取 \(cnt_j j\) 最大的 \(j\) 即可。
• \(\operatorname{lcm(i,j)}\le V\)：对于 \(1\le i,j \le 100000\) 的正整数对 \((i,j)\)，满足 \(lcm(i,j)\le V\) 的 \((i,j)\) 对数大概是 \(2.6\times 10^7\)（但是我不会证明。），直接暴力枚举。

把所有的 \(cnt_i i\) 扔进一个堆里，对于每个 \(i\) 每次取出最大的 \((cnt_j j)\)，如果 \(\operatorname{lcm(i,j)}\le V\) 直接退出（不减任何数一定比后面的都大）。

于是做到 \(O(2.6\times 10^7)\)？

code

pli b=*it;
if(!lcm(i,b.se)){ans=max(ans,1ll*i*cnt[i]+b.fi);break;}
else{ans=max(ans,1ll*i*cnt[i]+b.fi-cnt[lcm(i,b.se)]*min(i,b.se));} 

NOIP模拟赛T2 人门题(basis)

记这个主要是为了鸽很久的基环树吧。不过一些处理也很妙就是了。赛场想到的会略写。

description

给你两个序列 \(a\) 和 \(b\)。每次可以选择 \(a\) 中的任意个元素，令 \(a_i\gets b_{a_i}\)。问最少多少次操作可以使得序列不降。

solution

答案具有单调性所以二分。\(check(k)\) 时扫一遍 \(a\)，对于一个 \(i\)，\(a_i\) 的值即为 \(k\) 步内能到达的 \(\ge a_{i-1}\) 的最小值。

但是这个条件也太复杂了，不枚举很难求，考虑怎么转化。

对于一个 \(i\)，我们从 \(a_{i-1}\) 开始枚举，让 \(a_i=\) 第一个步数 \(\le k\) 的值，这样找出来的书等价于原来的条件。

注意到 \(V\le m\)，而因为单调不降的性质，一个值枚举到了不会再遇到，所以这里的枚举均摊 \(O(m)\)。

最后额步数怎么求。观察到这张图的结构一定是内向基环树森林，于是接下来是基环树基础操作恶补。

把边统一为 \((b_i,i)\)，转化为外向基环树森林。

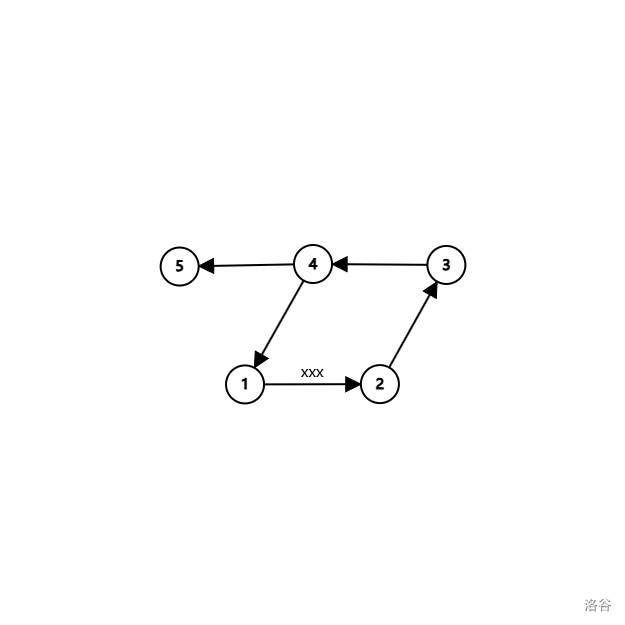
这是一棵基环树。一开始处理时，我们随便断掉环上的一条边（并查集是好做的）使其变成真正的树。这里假设断开的是 \((1,2)\) 那条边。

那么 \(u\) 到 \(v\) 的距离就分为了两种情况：

• \(u\) 只经过树边到达 \(v\)，此时 \(v\) 在 \(u\) 的子树内，直接 \(dep\) 计算即可。
• \(u\) 走到 \(1\)，经过断开的边 \((1,2)\)，\(2\) 走到 \(v\)。三段分开计算。

于是对于每一个连通块维护图中 \(2\) 这个点（也就是基环树的根），\(1\)（环上的最后一个点）不用再维护，就是 \(b_2\)。

额但是我觉得写起来比说起来难多了。细节贼几把多。

code

inline bool isa(int u,int v){return in[u]<=in[v]&&in[v]<=ot[u];}//v in u
inline int dis(int u,int v){//u to v?
	if(isa(u,v)) return dep[v]-dep[u];
	if(isa(u,b[rt[fd(v)]])) return dep[b[rt[fd(v)]]]-dep[u]/*+1*/+dep[v]/*-1*/;
	return inf;
}
inline bool chk(int x){
	int lst=0;
	for(int i=1;i<=n;i++){
		while(lst<=m&&dis(lst,a[i])>x) lst++;
		if(lst>m) return 0;
	}return 1;
}
inline void solve(){
	int l=0,r=m+1,md;
	while(l<r){md=(l+r>>1);if(chk(md))r=md;else l=md+1;}
	cout<<(l>m?-1:l)<<'\n';
}
signed main(){
	...
	for(int i=1;i<=m;i++){
		cin>>b[i];
		if(merge(i,b[i])) add(b[i],i);//并查集维护连通性
		else rt[fd(i)]=i;//维护每棵基环树的root
	}for(int i=1;i<=m;i++) (f[i]==i)&&(dfs(rt[i],0),1121);
	solve();
	return 0;
}

ARC115E - LEQ and NEQ

solution

一眼容斥。设 \(dp_{i,j}\) 为前 \(i\) 个数，强制 \(j\) 对相邻数相等的方案数。

有转移：\(dp_{i,j}=\sum_{k=0}^{i-1} (dp_{k,j-i+k+1}\min_{l=k+1}^{i-1}a_k)\)。

答案即为：\(\sum_{j=0}^{n} (-1)^{j}dp_{n,j}\)。

这个 \(j\) 看起来太没用了，答案只关心它的奇偶性。所以考虑（套路地）把容斥系数放进 dp 值里。

于是设 \(dp_i\) 表示只考虑前 \(i\) 个数的答案。

我们有 \(dp_i=\sum_{j=1}^{i-1}(dp_j \times \min_{k=j+1}^{i}a_k\times (-1)^{i-j-1})\)。

我们使用单调栈找到 \(i\) 之前第一个 \(\le a_i\) 的位置 \(k\)，对于 \(k\) 之前的位置，变的只有容斥系数这一项，具体来说就是由 \((-1)^{k-j-1}\) 变成了 \((-1)^{i-j-1}\)，所以系数变化即为：\(\times (-1)^{k+i}\)。

而对于 \([k,i-1]\) 的部分，最小值就是 \(a_i\)，我们按照 \(j+1\) 的奇偶性维护 \(dp_j\) 的前缀和 \(s\)，让容斥系数只跟 \(i\) 相关，系数 \(\times(-1)^i\) 即可。

于是最终的转移就是：

\[dp_i=dp_k\times(-1)^{i+k}+a_i (s_{i-1}-s_{k-1})\times (-1)^{i} \]

code

理清楚了并不是很难写。一些实现细节：

• 初值 \(dp_0=1\)。
• 当一个 \(i\) 不存在 \(k>0\) 时，只能转移后一部分。原因是我们并不需要 \(dp_0\) 这一项的贡献。想了很久。
• 学的题解定义 \(f_i=dp_i\times (-1)^i\)，使得式子代码均极为简洁，但我不是智慧人类所以看不懂不直观式子。

while(tp&&a[stk[tp]]>a[i])tp--;
int k=stk[tp];
if(!k) dp[i]=1ll*(i&1?mod-1:1)*a[i]%mod*s[i-1]%mod;
else dp[i]=1ll*(i&1?mod-1:1)*ad(1ll*dp[k]*(k&1?mod-1:1)%mod,1ll*a[i]*ad(s[i-1],mod-s[k-1])%mod)%mod;
s[i]=ad(s[i-1],1ll*dp[i]*(i&1?1:mod-1)%mod);
stk[++tp]=i;

P11338 [COI 2019] LJEPOTICA

你妈的啊，高精度减法写错了调一小时。一眼数位 dp。

首先差分一下，于是最终答案就是 \([1,R]\) 的答案减去 \([1,L-1]\) 的答案。

那么只需要计算可以到达的编号 \(\le lim\) 的叶子节点的编号和。

设 \(f_{i,j,0/1}\) 表示（从根）走到第 \(i\) 层节点，使用了 \(j\) 次操作，当前的编号顶 / 不顶上界，前 \(i\) 位的编号和。

但是算前 \(i\) 位编号和的时候需要知道当前有多少种不同的编号才能计算第 \(i\) 位编号和贡献。所以再记一个 \(dp_{i,j,0/1}\) 表示当前有多少种不同的编号。

设下一位是 \(p\)，转移时通过 \(j\) 的奇偶性可以分析出若当前不操作，\(p\) 是 \(0\) 还是 \(1\)（下一层如果不操作会走到的节点），按照 \(p\) 和 \(lim\) 下一位的关系，分类讨论顶不顶上界的情况进行转移。写起来会有点繁琐，但是如果理清楚了不是很难。

这题有个很恶心的点在于进入根节点之前可以无消耗地操作一次。也许有更优雅的做法但是我只会很蠢的分类。

大概就是按照原来的行动策略 dp 一次算出答案，把行动策略全部反向再 dp 一次，两次答案相加即可。

关于算重：因为必须答案操作恰好 \(k\) 次，而一个节点不能反向两次，所以不可能反向出完全相同的行动序列。

NOIP模拟赛T2 网格染色(grid)

这种典题不会做真的很有问题啊。哎这怎么不会做啊？？？

description

给你一个 \(n\) 行 \(10^9\) 列的网格图，有 \(m\) 次操作，每次会把第 \(p\) 行的 \([l,r]\) 涂黑。问：使剩余的行满足，任意相邻两行都存在至少一列被同时染黑，最少需要删掉几行。输出方案。

solution

设 \(dp_i\) 表示答案。有转移：\(dp_i=\min (dp_j+i-j-1)\)。

把跟 \(j\) 有关的项提出来：\(dp_i=\min(dp_j-j)+i-1\)。

染黑段数总和是 \(m\)，于是把 \(dp_i-i\) 挂在所有第 \(i\) 行染黑的格子上，查询时把所有染黑段的答案取最优。

离散化后用支持区间推平、区间求 \(\min\) 线段树维护，实现都是典典典。复杂度 \(O(n\log n)\)。

NOIP模拟赛T2 方可特尔(functor)

咦，小清新题。

description

\(n\le 10^6,m\le 2\times 10^6\)。

solution

欸 \(n,m\) 同阶，所以直接对于 \(1\le i \le n\) 的每个 \(i\) 求出答案。

设 \(p_{k}\) 是子序列长度为 \(k\) 时最优的排列。

结论：\(p_k\) 一定是 \(p_{k-1}\) 中插入一个数。

简略证明：

假设 \(p_k=\{1,2,3,5\},p_{k-1}=\{1,2,4\}\)。现在我们证明 \(p_k'=\{1,2,3,4\}\) 一定更优。

同时删掉 \(3\)，我们有 \(\{1,2,4\}\) 比 \(\{1,2,5\}\) 更优。那么加上 \(3\) 也一定是 \(p_k'\) 更优。

嗯所以我们动态维护 \(p\)。

设 \(cnt_i\) 为当前 \(p\) 中有多少个数比 \(i\) 小，那么加上一个 \(i\) 的贡献为：

\[a_i\times x^{cnt_i}-\sum_{j>i}(a_j\times x^{cnt_j}-a_j\times x^{cnt_j+1}) \]

每次取贡献最大的数加进去即可。于是考虑怎么维护这个贡献。

设 \(i\)，取出来时的贡献是 \(b_i\)，哎我也不知道怎么推出来的，反正对于 \([1,i-1]\) 区间 \(-(a_i-a_i\times x)\)，\((i+1,n)\) 区间 \(\times x\)。你可能会问那更后面的数对它前面的数的贡献不会变吗，然而因为放进去的是当前贡献（包含了后面的贡献的某些部分），所以后面的贡献全部可以抵消？？？？？？。。。。我不会推式子。

实现又是典典典。submission。

P5298 [PKUWC2018] Minimax - 洛谷

人类智慧。

答案那一坨看起来太难维护了，于是考虑离散化后对于每个 \(V\) 求出对应的 \(D\)。

设 \(L,R\) 是 \(u\) 的两个儿子， \(dp_{u,j}\) 为点 \(u\) 的权值是 \(j\) 的概率。那么对于 \(L\) 有转移（\(R\) 同理）：

\[dp_{u,j}\gets dp_{L,j}(p_i\times \sum_{k=1}^{j-1}dp_{R,k}+(1-p_i)\sum_{k=j+1}^{V}dp_{R,k}) \]

若 \(u\) 是叶子那么初值就是 \(dp_{u,p_i}=1\)。

复杂度 \(O(n^2)\)。考虑我们多维护了什么不需要的东西。我们发现 \(dp_u\) 中有值的位置只有 \(u\) 子树内的叶子数个。

我也不知道怎么想到的，反正尝试转移用线段树合并优化。

设需要合并的两棵线段树当前节点为 \(x,y\)，当前区间为 \([l,r]\)：

• \(x,y\) 均为空：直接返回。
• \(x\) 为空：此时维护的 \(dp_{x,[l,r]}=0\)，所以对 \(dp_{y,[l,r]}\) 的乘贡献可以转化为 \(p_i\times \sum_{k=1}^{l-1}dp_{x,k}\)（前缀和扣掉 \([l,r]\)）加上 \((1-p_i)\sum_{k=j+1}^{V}dp_{x,k}\)（同理）。 于是给 \(y\) 区间打上述乘法 \(tag\)。
• \(y\) 为空：同理。
• 均不为空：分别递归合并左右子树。

问题在于怎么维护 \(x,y\) 分别的“扣掉当前区间的前 / 后缀和”。神仙发现是线段树递归的过程中就可以维护这两样东西：递进左儿子就后缀和加上右儿子的和，递进右儿子就前缀和加上左儿子的和。

所以我们只需要一个支持单点加、区间乘、查询区间和的线段树。小细节是必须用合并子树之前的前 / 后缀和。

int p,px_=ad(px,tr[tr[x].ls].sum),py_=ad(py,tr[tr[y].ls].sum);nwn(p);
tr[p].ls=merge(tr[x].ls,tr[y].ls,l,mid,px,ad(sx,tr[tr[x].rs].sum),py,ad(sy,tr[tr[y].rs].sum),val);
tr[p].rs=merge(tr[x].rs,tr[y].rs,mid+1,r,px_,sx,py_,sy,val);

T2 ？？？

哎第一步都想不到。但确实人类智慧题。

description

给你一个长为 \(n\) 的序列 \(a\)，你需要找出一个长度为 \(k\) 的子序列 \(b_1,b_2,\cdots,b_k\) 使得 \(\max(b_1+b_2,b_2+b_3,\cdots,b_{k-1}+b_k,b_k+b_1)\) 最小，求这个最小值。

solution

最大值最小，考虑二分。设当前二分的值为 \(x\)。

容易观察到所有 \(a_i\le \frac{x}{2}\) 的 \(i\) 都可以选。

那么剩下的数一定不能连续选两个，也就是说在我们已经选的数中两两之间只能插入最多一个剩下的数。

所以对于已选的数找到两两之间的最小值，再判断能不能插入即可。上述过程都可以扫一遍的时候直接全部做完。

于是做到 \(O(n\log n)\)。

T3 ？？？

description

给你一个长为 \(2n\) 的序列 \(p\)，其中 \([1,n]\) 的数正好各出现两次。现要求给每对相同的元素赋同一种括号 ( 或 )，使得最终序列是合法的括号序列，若有解输出字典序最小的序列。

\(n\le 2\times 10^6\)，1s。

incomplete solution

嗯对就是过不了的赛时做法。

容易发现如果要有解，那么必须保证：

• 每个前缀的已填右括号数量不超过区间的一半。
• 每个后缀的已填左括号数量不超过区间的一半。

不超过一半可以经典 trick 转化为 \(1,-1\)。线段树维护最大前缀后缀和，从小往大扫，每次先尝试填入左括号，若不合法则填入右括号，仍然不合法就无解。

复杂度 \(O(n\log n)\)，额但是线段树过不了。

solution

拜谢奶队。

设取了左括号位置的序列为 \(\{b_1,b_2,\cdots,b_n\}\)。

那么如果最终括号序列合法，这个序列一定被 \(\{1,3,5,\cdots,2n-1\}\) 偏序。证明参考上一个做法。

证明：

• 必要条件：不被偏序的那个位置的前缀的右括号数量一定超过一半。
• 充分条件：在这种情况下一定满足“每个后缀的已填左括号数量”

于是使用一个 set 维护 \(\{1,3,5,\cdots,2n-1\}\)，每次取出 \(i\) 和 \(to_i\)（和 \(i\) 匹配的位置），找到剩余位置中比它们大的第一个位置删掉（相当于 \(i\) 和 \(to_i\) 被这个位置偏序）。如果剩余位置中没有比 \(i\) 大的说明无解（因为后面的不会有比 \(i\) 更小的可以被偏序）。

模拟即可。

P9485 「LAOI-1」积水

不是哥，绿题这么难？。

description

给你一个抽象的一维地面，每格地面有高度 \(a_i\)，每格上初始有 \(inf\) 深度的水。在地面的低洼处会积水。

现在你可以修改一格地面的高度，要求最小化积水深度总和。

solution

设 \(pre_i\) 为 \([1,i]\) 中 \(a_j\) 最大的 \(j\)，\(suf_i\) 为 \([i,n]\) 中 \(a_j\) 最大的 \(j\)。

那么积水高度 \(h_i=\max(0,\min(pre_{i-1},suf_{i+1})-a_i)\)。

考虑怎么操作最优。

• 提高一格地面的高度。此时对于其它格来说积水深度一定不降。对于抬高的这一格，我们只需要把它抬到 \(\min(pre_{i-1},suf_{i+1})\) 就可以让它不积水。容易发现这时对于其它格来说没有增大深度，所以答案少的就是 \(h_i\)。
• 降低一格地面的高度。这种操作可能发生当且仅当 \(pre_i=i\) 或 \(suf_i=i\)。这里只讨论的 \(pre_i=i\) 情况。对于当前格来说，答案会变成 \(\max(0,\min(pre_{i-1},suf_{i+1})-a_i')\)。如果 \(a_i'< a_{pre_{pre_{i-1}-1}}\)，那一定是不优的，因为这时其它格的答案并不会因此变得更小，但是当前格的答案可能因此变得更大。在此基础上，\(a_i'\) 降低的越多答案肯定降低的越多。感性理解就是，变得越矮它是较小值的情况就越多，于是答案随着它变化的幅度就越大。所以，如果要降低一格是前缀最大值的地面，一定是把它降到它之前的前缀最大值高度。

第一种答案随便统计。

第二种考虑对于每一格计算它对于它的前缀 / 后缀最大值位置的贡献。需要注意的是，并不能直接把用上一个最大值，还要跟当前最大值到当前位置这段区间取 \(\max\)。

还是以前缀来说，式子就是 \(pre_{i-1}'=\max(a_{pre_{pre_{i-1}-1}}, \max _{j=pre_{i-1}}^{i-1} a_j)\)。也就是还要多维护一个区间最大值。

code

好多细节。

(i>1)&&(ls[pre[i-1]]+=max(0,min(max(a[pre[pre[i-1]-1]],qry(pre[i-1]+1,i-1)),a[suf[i+1]])-a[i])-h[i]);
(i<n)&&(rs[suf[i+1]]+=max(0,min(max(a[suf[suf[i+1]+1]],qry(i+1,suf[i+1]-1)),a[pre[i-1]])-a[i])-h[i]);

additional solution

容易发现每个前缀 / 后缀最大值所影响的区间是均摊 \(O(1)\) 的，所以可以考虑对于每个最大值直接扫一遍统计答案，理论上可以做到 \(O(n)\)。但是这太不直观了，我只会套路做法。

线段树进阶2 HDU5302 Gorgeous Sequence 势能线段树

其实写了一天势能线段树，感觉如果不写势能分析没啥好写记录的。但是势能分析我不会。记录这些东西我也不知道为啥。

description

给你一个序列，需要支持以下操作：

1. 区间取 \(\min\)（把比 \(x\) 大的数覆盖成 \(x\)）。

2. 区间求 \(\max\)。

3. 区间求和。

\(n,q\le 10^6\)。

solution

以下的 \(x\) 均为操作一中的 \(x\)。

首先不考虑操作三。

使用线段树维护：区间最大值 \(fx\)，区间次大值 \(sx\)，区间最大值的懒标记 \(tag\)，以及区间和 \(sum\)。查询随便做。

考虑更新对于这几个值的影响。

• \(x\ge fx\)：没影响。
• \(sx\le x < fx\)：\(fx\gets x\)，即给该区间的最大值打标记覆盖成 \(x\)。
• \(x<sx\)：两个值均会被更新，递归进子树处理。

写起来没什么难度。但是复杂度证明咕咕咕了。

P4314 CPU 监控 历史最大值线段树

感觉 luogu 题解区不是矩阵写法的都读不懂。最后是随便找了一篇博客园的抄了 ta tag 的定义自己推的。

description

给你一个序列，你需要支持区间加、推平、求最大值、求历史最大值操作。\(n\le 10^6\)。

solution

考虑如果按照没有区间最大值的方法直接做会怎么样。也就是直接多维护一个单点历史最大值、历史最大的 tag。这样一定会出问题，因为你不能确定当前点历史最大 tag 往儿子更新的时候这些操作的先后顺序以及是否多算。

设 \(mx\) 是当前点最大值，\(hx\) 是当前点历史最大值，\(ta\) 是 add_tag，\(tc\) 是 cov_tag。

先解决一个小问题：既有 add_tag，又有 cov_tag 实在是太麻烦了。我们想通过一些手段使得同时最多只有一个 tag 的值是需要维护的。我们发现其实是可以的，因为第一次 cover 会覆盖掉原来的所有操作，同时后面的 add 可以直接加到 cov_tag 上。于是非常巧妙的只剩下了一个 tag。

接着考虑 pd 的时候操作的先后顺序、算重问题怎么解决。我们先把历史最大的 tag 拆成两个：历史最大的 \(ta\) 是 \(ha\)，历史最大的 \(tc\) 是 \(hc\)。可这样似乎仍然没法解决原来的问题。于是更改定义：\(ha,hc\) 为上次 pd 后的最大 \(ta/tc\)。这简直是太聪明了。因为维护的是上次 pd 后的操作序列最大前缀，所以这些操作一定没有被下传到儿子且应该在儿子操作序列的后面。

其实思路已经讲完了，但是记一下 pd 细节。设当前点的是 \(q\)，它的一个儿子是 \(p\)。因为是历史最大肯定都要跟自己取 \(\max\)，下文省略。

\(hx_p\gets \max(mx_p+ha_q,hc_p)\)。历史最大和可以由 \(p\) 完整的操作序列拼上 \(q\) 上次 pd 之后的历史最大和，或直接由 cover_tag 得出。

\(ha_p\gets ta_p+ha_q\)。历史最大和可以是当前完整的操作序列拼上 \(q\) 的历史最大和。本条可以转移当且仅当 \(p\) 没有被 cover 过，否则 \(ta_p\) 并不是当前完整的操作序列。

\(hc_p\gets \max(hc_p+ha_q,hc_q)\)。跟上一条基本相同，只是多了一个父亲的最大覆盖转移。同理，第一项可以转移当且仅当 \(p\) 被 cover 过。

注意按照定义，这样转移完之后 \(ha_q,hc_q\) 要清空。

code

较为难写。

inline void cha(int p,ll x){mx[p]+=x;chkx(hx[p],mx[p]);ta[p]+=x;chkx(ha[p],ta[p]);}
inline void chc(int p,ll x){mx[p]=x;chkx(hx[p],mx[p]);tc[p]=x;chkx(hc[p],tc[p]);}
inline void pusha(int p,ll x){if(tc[p]>lnf_){chc(p,tc[p]+x);}else{cha(p,x);}}
inline void pushc(int p,ll x){ta[p]=0;chc(p,x);}
inline void upd_(int p,int q){
    chkx(hx[p],max(mx[p]+ha[q],hc[q]));
    (tc[p]==lnf_)&&(chkx(ha[p],ta[p]+ha[q]),1121);
    chkx(hc[p],max(tc[p]>lnf_?tc[p]+ha[q]:lnf_,hc[q]));
}//update hx,ha,hc
inline void clr(int p){ha[p]=0,hc[p]=lnf_;}
inline void pushd(int p){
    upd_(ls,p);upd_(rs,p);clr(p);
    if(tc[p]>lnf_){pushc(ls,tc[p]),pushc(rs,tc[p]);tc[p]=lnf_;}
    else if(ta[p]){pusha(ls,ta[p]),pusha(rs,ta[p]);ta[p]=0;}
}

P14084 「CZOI-R7」敲击

设 \(cnt_i\) 是原串长度为 \(i\) 的前缀中 \(1\) 的个数。

设 \(dp_{i,j}\) 为考虑了前 \(i\) 段，第 \(i\) 段有 \(j\) 个 \(1\) 的方案数。

考虑类似数位 dp 的思想，从高位到低位枚举第几段第一次使得二进制意义下的数小于 \(L\)，相当于固定一段前缀，后面再进行没有限制的 dp。

那么有：

\[dp_{0,j+cnt_w}\gets \binom{n-i}{j} \]

注意到如果我们选择的段不是第一段，那么这一段前面必然会有一段原串，因此还需要保证那一段里 \(1\) 的个数 \(\le m-cnt\)。

直接分类讨论。把第一段第一次小于 \(L\) 的 dp 数组设为 \(f\)（定义同），其它还是 \(dp\)。

答案就是：

\(Ans=\sum_{i=0}^{m}f_{n,i}+\sum_{i=0}^{n}\sum_{j=0}^{m}dp_{i,j}\)。

使用矩阵乘法优化 dp。

如果我们按照常规方法维护 \(\begin{bmatrix}dp_{i,0},dp_{i,1},\cdots,dp_{i,m}\end{bmatrix}\)，却没有办法计算对于每一个 \(i\) 的 \(\sum dp_{i,j}\)。于是直接在矩阵中多维护一个 \(s_i\) 表示前缀 \(i-1\) 的 \(\sum dp_{k,j}\)。

于是做完了，复杂度 \(O(n^3 \log m)\)。

corner case：

• 如果我们枚举的段在第二段以后，我们需要保证前两段的合法性，即 \(2cnt_n\le m\)。不难发现这个和枚举的段正好是第二段的转移可以 merge。

• 如果原串合法，那么我们会少统计这个答案，因为我们只计算了小于的情况。加上就好。

code

对于 \(f\) 和 \(dp\) 来说，它们后面的转移是没有区别的。所以直接预处理出它们后面的转移矩阵。

转移次数需要好好推推，实现细节挺多的。

submission。

UOJ#169. 【UR #11】元旦老人与数列

无敌融合怪，\(1+1>2\) 的难调，吃了三天。

关于吉司机线段树的写法

写这题时发现之前的吉司机写法有可以优化的地方。当时维护了一个最大值的 cover_tag，但是这个记录是多余的。因为你发现全程使用的时候它的值都和当前最大值本身没有区别。同时不难发现 tag 本身“记录有没有被打过标记”在这个情景下也是无用的。所以直接扔掉这个少维护一个值。不过历史 cover_tag 还是要维护的，毕竟要保障这个值出现在在上次 pd 后。

solution

取 \(\max\) 的部分使用吉司机线段树，历史和使用维护操作序列的 trick。

所以我们需要把最大值和非最大值分开维护。需要维护的值有：

• 最小值、次小值、历史最小值 \(fn,sn,hn\)
• 当前的 add_tag \(ta\)。
• 上次 pushdown 之后的其它值的最大 add_tag、最大值的最大 cover_tag \(ha,hc\)。

想清楚定义之后不是很难写（吧？但是很难调。）。

submission。

P3292 [SCOI2016] 幸运数字 - 洛谷

顺便记录一个极其优雅的求区间线性基的方法。

solution

合并线性基是 \(O(\log^2n)\) 的。

设 \(A=lca(x,y)\)。

预处理 \(x\) 到它的第 \(2^i\) 级祖先的线性基。直接从 \(x,y\) 分别往上倍增的复杂度是 \(O(n\log^3n)+O(q\log^3n)\)，因为 \(q\) 很大，显然无法通过。但是注意到线性基具有 RMQ 的性质，也就是说多次插入同一个数并不会影响答案。所以可以类似 st 表的做法得出 \([x,A],[y,A]\)（这里的区间指树上的链）的线性基再 merge 起来即可计算答案。时间复杂度 \(O(n\log^3n+q\log^2 n)\)，空间复杂度 \(O(n\log^2n)\)。

嗯但是这不够优雅。

我们强制让线性基的每个代表元维护元素深度最小的点。

关于如何插入：

设插入的数是 \(x\)。

在常规插入之前，如果当前位的代表元的深度小于 \(x\) 的深度，那么就把 \(x\) 替换当前代表元，并让当前位代表元代替 \(x\) 继续插入。（即 \(swap(p_i,x)\)。）看起来很对。

这时线性基就支持删除一段深度为前缀的元素了。只需要把深度 \(<lim\) 的代表元清空即可。同时因为我们维护的永远是深度最大的点，所以不会有删掉多余元素的情况。

剩下比较显然。对于每个点预处理根到它的线性基，合并 \(x,y\) 分别到根的线性基，删除深度 \(<dep_{lca(x,y)}\) 的元素即可。时间复杂度 \(O(n\log n+q\log ^2n)\)，空间复杂度 \(O(n\log n)\)，非常的牛。

code

线性基部分：

struct Xb{
	pli p[maxl];
	inline void ins(pli x){
		for(int i=mxl;i>=0;i--){
			if(!(x.fi>>i&1)) continue;
			if(p[i].fi){(p[i].se<x.se)&&(swap(p[i],x),418);x.fi^=p[i].fi;}
			else{p[i]=x;return;}
		}
	}//插入
	inline Xb del(int lim){Xb ans;for(int i=mxl;i>=0;i--)ans.p[i]=(p[i].se>=lim?p[i]:emp);return ans;}//删除一段前缀
	inline ll qry(){ll ans=0;for(int i=mxl;i>=0;i--){((ans^p[i].fi)>ans)&&(ans^=p[i].fi);}return ans;}//最大值
}o[maxn];

P6772 [NOI2020] 美食家

感觉这个做法好萌啊。

因为 \(w_i\le 5\)，不难想到把每个点拆成 \(5\) 个点 \(id_{i,0},id_{i,1},\cdots,id_{i,4}\)，代表距离 \(i\) 多远的一个点，这样就把图拆成了一个边权为 \(1\) 的图。

设 \(dp_{t,i}\) 为花费了恰好 \(t\) 的时间，现在在 \(i\) 的最大答案。转移和矩乘优化都是简单的。

但是 \(k\) 个活动那里没有办法计算，所以只能在每两个活动之间快速幂。复杂度是 \(O(k(5n)^3\log T)\)，直接爆炸。

此时回到矩阵乘法优化 dp 的原点。你发现如果只是维护一行 dp 值，转移一次（乘一个转移矩阵）的复杂度是 \(O(n^2)\) 的。所以原算法的瓶颈在于每次快速幂时都要重新算转移矩阵的幂次。所以考虑预处理出矩阵快速幂中用到的转移矩阵的 \(2^i\) 次幂。于是复杂度降至 \(O((5n)^3\log T+k(5n)^2\log T)\)。