HLSL中的MUL指令深层剖析

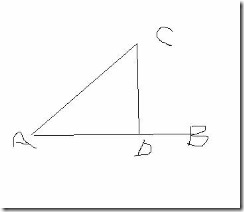
原作者邮箱 BoYueGame#Gmail#com 欢迎交流。
此贴可以随意转载而不用注名出处。但也别说是你写的就行。
在读此文之前，读者应该知道什么是行主，列主矩阵，写过简单的HLSL或者ASM SHADER
读者知道简单的矩阵运算规则
本文主要内容有：
一、部分背景内容
二、HLSL中的row-major matrix picking and column-major matrix picking
三、MUL规则
四、观察矩阵的另类解释和TBN空间的类推
五、HLSL中矩阵的构造（为什么WorldToTargentSpaceMatrix要左乘LightDir）
 
一、部分背景
既然是HLSL中的指令，那我们的所有标准就以D3D而来。换句话说，矩阵以如下方式存储
１１ １２ １３ １４
２１ ２２ ２３ ２４
３１ ３２ ３３ ３４
４１ ４２ ４３ ４４
典型的世界矩阵如下
C1 C2 C3 C4
R1 １ ０ ０ ０
R2 ０ １ ０ ０
R3 ０ ０ １ ０
R4 ２０ ２０ ２０ １
这就是传说中的行主矩阵（row-major matrix） 注：这里只说它的存储方式，而不管他的运算符操作方法。
对于一个这样的矩阵，我们给一个行向量（row vector） V(X,Y,Z,W)
那么，V*M为如下结果
X = X*11+Y*21+Z*31+W*41 （１）
Y = X*12+Y*22+Z*32+W*42 （２）
Z = X*13+Y*23+Z*33+W*43 （３）
W = X*14+Y*24+Z*34+W*44 （４）
看到上面的1,2,3,4四个运算，我们很自然想到了向量点乘（Dot Product）我们把三维向量的点乘简称dp3，四维的则叫dp4 那么有
dp3（V1，V2）= V1.x*V2.x+V1.y*V2.y+V1.z*V2.z
dp4（V1，V2）= V1.x*V2.x+V1.y*V2.y+V1.z*V2.z+V1.w*V2.w
于是，我们的向量V乘矩阵M就可以表示为
V.X = dp4（V，M[C1]）；
V.Y = dp4（V，M[C2]）；
V.Z = dp4（V，M[C3]）；
V.W = dp4（V,M[C4]）；
说了这么多，好像不是在说MUL指令，但其实这个MUL指令息息相关。
首先来看看Mul(x,y)指令的最基本的信息。
当X为向量时，X被视为行向量。
当Y为向量时，Y被视为列向量。
大家都知道，在HLSL中，如果我们采用Effect::SetMatrix进行矩阵的设置时，我们就可以采用如Mul（inPos，matWorldViewProj）来计算。 
而如果是用普通的SetVertexConstantF等来设置矩阵数据的话，就需要用Mul（matWorldViewProj，inPos）来计算，
或者用Mul（inPos，matWorldViewProjTranspose）。
我想许多人都明白，那是因为在用SetMatrix时，HLSL会将矩阵进行转置，进而成为一个列矩阵。
自然，采用SetMatrix与不采用SetMatrix就不一样了。
可是，我们之前不是说了么，行向量乘以行主矩阵才是 向量在左边呀， 但现在一个是行向量，一个是列矩阵。 
怎么就绕不过来了呢。 
其实很容易绕过来，要知道MUL是我们（或者说叫他们）自己定义的，怎么实现难道还非得按照标准的线性代数规则来安排位置不成。
用HLSL写过SHADER的人都应该清楚下面这段代码的含义。
float4x4 matViewProjection;
float4 vs_main(float4 Position : POSITION0) : POSITION0
{
return mul( Input.Position, matViewProjection );
}
//其对应的汇编代码如下
// matViewProjection c0 4
//
vs_2_0
dcl_position v0
dp4 oPos.x, v0, c0
dp4 oPos.y, v0, c1
dp4 oPos.z, v0, c2
dp4 oPos.w, v0, c3
是不是觉得dp4很亲切呢。对了，就是它。 这意思就是说，我们的c0,c1,c2,c3存放着我们先前讲到的C1 C2 C3 C4。 这就是我们的背景内容，
到此结束。 下面将展开一系列的为什么。
而如下的HLSL代码
float4x4 matViewProjection;
float4 vs_main(float4 Position : POSITION0) : POSITION0
{
return mul(matViewProjection，Input.Position );
}
对应的ASM SHADER如下
mul r0, v0.y, c1
mad r0, c0, v0.x, r0
mad r0, c2, v0.z, r0
mad oPos, c3, v0.w, r0
由此可以看出 此时的C0－C3存放的是一个行矩阵。在此仅为证明 mul(向量，矩阵) 与 mul(矩阵，向量)不是一个东西。
二、HLSL中的row-major matrix picking and column-major matrix picking
HLSL在将矩阵赋值给常量寄存器的时候。有两种方式，一种是每个常量寄存器存放一行的数据，另一种是每个常量寄存器存放着一列的数据。
默认是按列选取（column-major matrix picking）。 
假设有一个矩阵M，其存放位置是从C0寄存器开始。 那么如果我们按行选取（row-major picking）则有
C0 = 11 12 13 14
C1 = 21 22 23 24
C2 = 31 32 33 34
C3 = 41 42 43 44
如果我们按列选取（col-major picking）则有
C0 = 11 21 31 41
C1 = 21 22 32 42
C2 = 31 32 33 43
C3 = 41 42 43 44
三、MUL规则
有了上面的的了解，我们就可以很容易地知道，MUL到底用什么。当然是取决于这两种选取规则。下面我们就逐一讨论。 
在此依然要声明一下， 我们程序中的矩阵是按D3D标准存放。
１、采用SetMatrix, 采用按列选取（col-major picking）
在这样的方式下，若我们将C0－C3按如下排开
C0
C1
C2
C3
则它是一个转入矩阵的转置矩阵。即Cx为先前矩阵的x列
而由我们先前提到的MUL（向量，矩阵）的ASM代码可以得出。 这正是我们想要的。
dp4 oPos.x, v0, c0
dp4 oPos.y, v0, c1
dp4 oPos.z, v0, c2
dp4 oPos.w, v0, c3
于是，在这种方式下，我们采用的是MUL（向量，矩阵）
２、采用SetMatrix,采用按列选取(row-major picking)
在这样的方式下，我们得到的和设置前的矩阵一样。 由此看来，我们得到的矩阵与按行存储的矩阵刚刚是一个转置。 既然是这样，
那大家回忆一下矩阵运算法则
A*B ó BT*AT 
这里若A*B对应的是Mul(向量，矩阵). 其中A为行向量即1Xn的矩阵，矩阵为nXm
那么Mul(矩阵，向量)则真好对应了上面的公式。
注：当向量作为第二个参数是，是一个列向量，即n X 1矩阵
所以，在这种方式下我们采用的是Mul(矩阵，向量)
３、不采用SetMatrix,采用按列选择。
在这样的方式下，相对于一方按，得到的矩阵和2方案相同。
４、不采用SetMatrix,采用按行选择.得到的矩阵和1方案相同。
四、观察矩阵的另类解释和TBN空间的类推
在D3D SDK文档中有一份这样的公式。讲述的是
D3DXMatrixLookAtLH
函数生成的东西。（这是一个左手观察系，采用D3D的行矩阵方式存储）
zaxis = normal(At - Eye)
xaxis = normal(cross(Up, zaxis))
yaxis = cross(zaxis, xaxis)
 
       C1              C2                 C3             C4  
 R1 xaxis.x           yaxis.x           zaxis.x          0
 R2 xaxis.y           yaxis.y           zaxis.y          0
 R3 xaxis.z           yaxis.z           zaxis.z          0
R4 -dot(xaxis, eye)  -dot(yaxis, eye)  -dot(zaxis, eye) 1
计算机图形学书上也讲了如何推导这个矩阵。但貌似依然没有给出为什么这样写就构成了观察矩阵了。 
首先明白观察矩阵的目的是：将一个世界空间的坐标转换到观察坐系中。　即将一个由X,Y,Z轴构成的世界空间的坐标点调整到由摄相机的
上向量、观察方向、右向量的空间中。　在这里，摄相机的右向量（上向量与观察方向的叉乘）等同于世界坐标系中的X轴。　上向量等同
于Y轴，观察方向等同于Z轴。然后，我们试着拿一个点与这个矩阵相乘。
V0*matView
按背景知识中讲到的，我们得到的一个点V1是。
V1.x = V0.x·matView[C1]
V2.y = V0.y·matView[C2]
V3.z = V0.z·matView[C3]
V4.w = V0.w·matView[C4]
 
上面式子中 ·表示dp4
 
在中学的时候我们就学过，点乘表示一个向量在另一个向量上的投影。好吧，我们要的就是这东西。

上面的图中（图太丑了，见笑）　AD即为AC在AB上的投影。
而-dot(xaxis, eye)  -dot(yaxis, eye)  -dot(zaxis, eye)　则是因为摄相机并不在原点，而我们在做投影变换的时候，以原点为观察参考
点会简化很多工作。所以我们的顶点要先把自己移回原点才行。而移的多少，正好是原点到摄相机的位置构成的一个向量在自己各个轴上
的投影。
　
于是，我们可以知道，乘以观察矩阵，　就相当于是把一个点以原点为起点，自己为终点，构造一个向量，然后求出自己在由摄相机的
各个轴构上的投影。最后再根据摄相机位置移回原点的过程。　由于我基本上不会画图，所以大家看起来有些吃力了。请各位见谅。　
但这并不是什么复杂的事情，只要用上点乘是投影的这个理念，自然就想明白了。
 
而我们模型中的T B N信息。按以下方式构造出来的矩阵，则刚好是由模型空间到切线空间的转换。
 
Tx Bx Nx
Ty By Ny
Tz Bz Nz
 
五、HLSL中矩阵的构造（为什么WorldToTargentSpaceMatrix要左乘LightDir）
在我们的NormalMapping等需要转换到切线空间的映射中，常常看到这样的代码
Float3x3 matWorldToTargent = {WorldT,WorldB,WorldN};
又或者
Float3x3 matWorldToTargent;
matWorldToTargent[0] = WorldT;
matWorldToTargent[1] = WorldB;
matWorldToTargent[2] = WorldN;
//float3 LightDir;
LightDirInTS = mul(matWorldToTargent,LightDir);
我也看到网上许多人问这个问题，并且我先前也不是懂。 因为看到的HLSL代码中，并没有出现row-major matrix picking和column-major 
matrix picking转换的代码，也就是说，默认为column-major matrix picking。 当然会想到，我们构造出来的矩阵，其对应的寄存器值正
好是
Cx = WorldT;
Cx+1 = WorldB;
Cx+2 = WroldN;
所以，它刚好是
Tx Bx Nx
Ty By Ny
Tz Bz Nz
的转置，
Tx Ty Tz
Bx By Bz
Nx Ny Nz
应该用LightDirInTS = mul(LightDir，matWorldToTargent);才对。
显然，我们被眼睛深深的欺骗了。
请看如下代码
float4x4 mat;
mat[0] = float4(1,2,3,4);
mat[1] = float4(5,6,7,8);
mat[2] = float4(9,10,11,12);
mat[3] = float4(13,14,15,16);
mul(mat,inPos);
对应的是
def c4, 1, 2, 3, 4
def c5, 5, 6, 7, 8
def c6, 9, 10, 11, 12
def c7, 13, 14, 15, 16
而若将指令改为mul(inPos,mat); 那么常量存放的值为
def c4, 1, 5, 9, 13
def c5, 2, 6, 10, 14
def c6, 3, 7, 11, 15
def c7, 4, 8, 12, 16
并且，上面的数据与HLSL中的矩阵数据picking方式无关。而对矩阵的操作，则都为dp4 pos,cx，也就是说对于mul(inPos,mat);的情况，
相当于是将其转置，再进行dp4操作。 而对于mul(mat,inPos);则是直接进行dp4操作。 而按我们想要的，则第一种情况才满足条件。
 第二种是因为优化导致的先转置再dp4，与前面提到的不转置进行类似于下面的操作是一样的。
mul r0, v0.y, c1
mad r0, c0, v0.x, r0
mad r0, c2, v0.z, r0
mad oPos, c3, v0.w, r0
若我们认定HLSL中构造矩阵是一个常量寄存器装一个mat[i]。即第一种情况。 那么此时想当于得到的是未经转置的矩阵，我们则认为，
T B N在构造后，形成的是一个
Tx Ty Tz
Bx By Bz
Nx Ny Nz
mul(mat,inPos);刚好满足要求。
若我们认定HLSL中构造矩阵的时候，一个常量寄存器不是装一个mat[i] 面是将构造他的float4的各个分量分别存。 即第二种情况。
那么得到的便是
Tx Bx Nx
Ty By Ny
Tz Bz Nz
 
我们想要它实现转换，则必须转置。 而由A*B ó BT*AT ，可知，mul(mat,inPos)即为所求。
第二种认定方案是比较容易让人接受的方案。
花了三个小时的时间来总结这几天纠结的问题，总算有一个收场。　其实还有一些关于RenderMonkey的问题，而有了上面的理解了，
那些已经不是问题了。待有空再继续总结。
附RenderMonkey控制面板