数学 Trick 之：双线 Catalan

能够解决的问题

形如这一类问题：从 \((0, 0)\) 到 \((n, m)\)，每次往上或右走，不能走到给定的两条直线。

优缺点

无

思路

首先，如果你不会单线做法，可以先看看 Catalan 的内容。

我们先回顾一下一条直线。

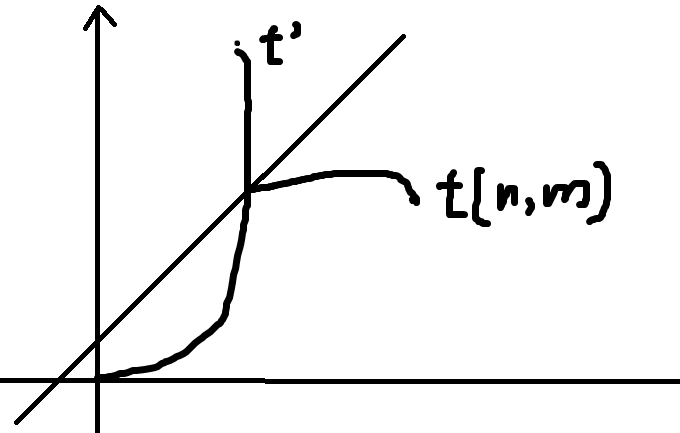
我们走了一个对称点来得到不合法的值，而且这里有一个重要性质：无论经过多少次直线，都可以通过走一个对称点来不重不漏地计数（下文称为 性质 \(1\)）。

我们考虑两条线的时候的不合法情况。

设两个直线为 \(l_1, l_2\)。

根据 性质 \(1\)，连续经过一条直线可以算作一次，所以我们可以把不合法情况表达为 \(A\)，\(B\)，\(ABA\)，\(BAB\)，\(BABAB\)，等（交替出现）。

此时我们考虑将目标点对 \(l_1\) 对称会怎么样。

此时有两种情况：

1. 最后一个经过的是 \(l_1\)，如图。

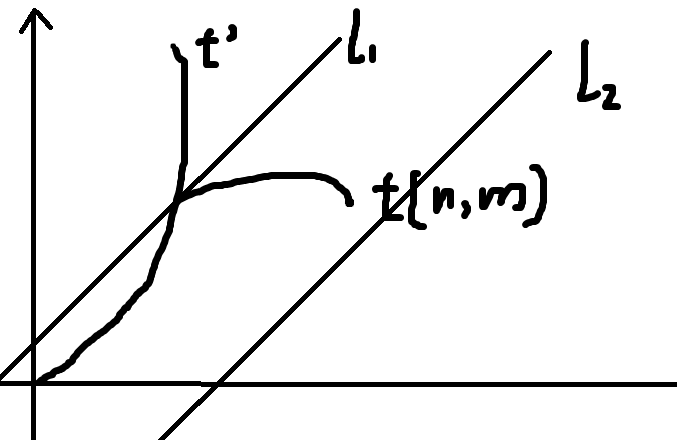
此时后缀为 \(A\)。

2. 最后一个经过的是 \(l_2\)（图中显然不合法，只是演示用，但是这种情况确实会发生，不理解的可以画图）。

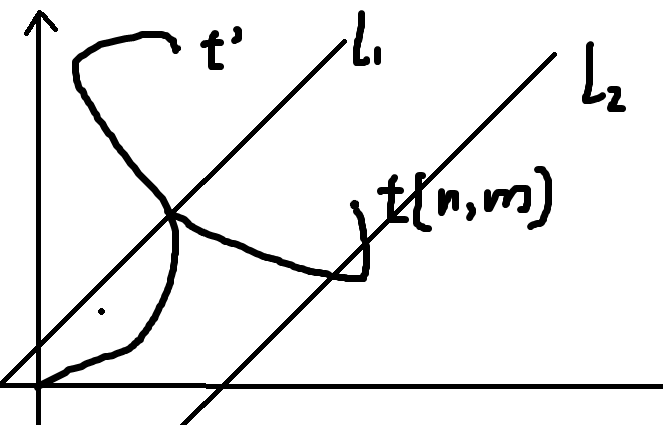
此时后缀为 \(AB\)。

综上，他统计后缀为 \(A\) 或 \(AB\) 的方案数。但是他无法统计后缀为 \(BB\) 的方案数。想要得到后缀为 \(BB\) 的方案数，我们关于 \(l_2\) 对称即可但是我们会算重一些方案，比如 \(BAB\)（既有后缀 \(AB\)， 又有后缀 \(B\)）。

那么，我们能不能求出只经过 \(A\) 或 \(AB\) 的值方案数（请注意，这里说的不是后缀）？我们考虑把关于 \(l_1\) 对称的点再关于 \(l_2\) 对称（如图），此时又有两种情况：

1. 最后一个经过的是 \(l_1\)，如图。

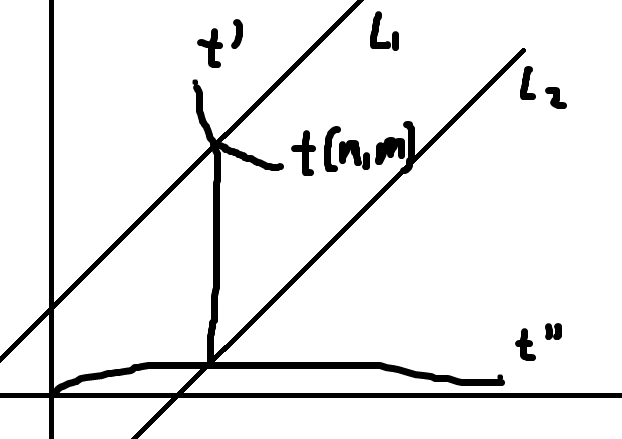
此时后缀为 \(BA\)。

2. 最后一个经过的是 \(l_2\)（图中不合法得更离谱了，只是演示用，而且这种情况也确实会发生，不理解的也可以画图）。

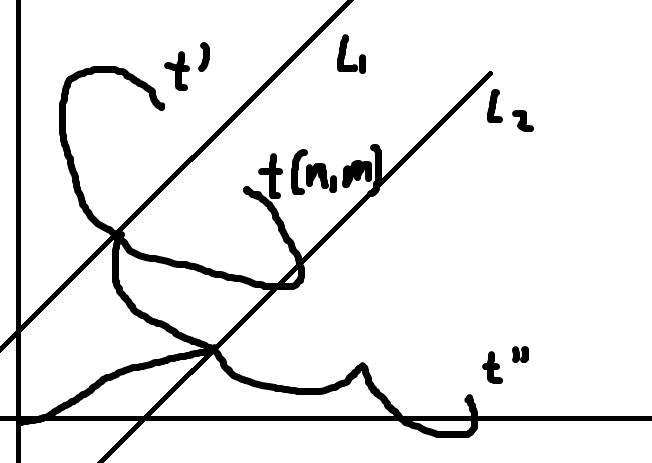
此时后缀为 \(BAB\)。

综上，他统计后缀为 \(BA\) 或 \(BAB\) 的方案数，而且我们发现，将结尾为 \(A\) 或 \(AB\) 的方案数减去结尾为 \(BA\) 或 \(BAB\) 的方案数，就得到了只经过 \(A\) 或 \(AB\) 的方案数！

同理，再关于 \(l_1\) 对称，得到后缀为 \(ABA\) 或 \(ABAB\) 的方案数，再关于 \(l_2\) 对称，得到后缀为 \(BABA\) 或 \(BABAB\) 的方案数，相减，得到只经过 \(ABA\) 或 \(ABAB\) 的方案数，以此类推，直到当前点不在第一象限即可。

那么我们就解决了 \(A\)，\(AB\)，\(ABA\)，\(ABAB\)，\(ABABA\)，\(ABABAB\) 等为后缀的方案数，此时还剩下 \(B\)，\(BA\)，\(BAB\)，\(BABA\)，\(BABAB\)，\(BABABA\) 等为后缀的方案数，而这些和前面几乎一模一样，只需要先关于 \(l_2\) 对称即可。

于是我们就解决了这类问题。

例题

Luogu P3266 [JLOI2015] 骗我呢

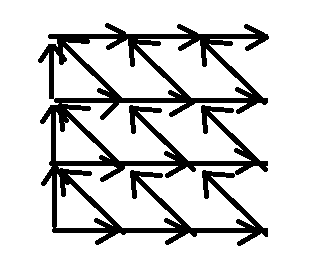
这道题的 dp 部分比较简单，观察到每行 \(m\) 个数且值域为 \(0 \sim m\)，有 \(m + 1\) 个数，所以定义 \(dp_{i,j}\) 表示当前选到第 \(i\) 行，这行不选 \(j\) 的方案数，转移非常简单，直接写了： \(dp_{i,j}=\sum_{k=0}^{j+1​}dp_{i−1,k}\)，而且我们发现右边的东西就等于 \(dp_{i−1,j+1}+dp_{i,j−1}\)，可以看作走路径（如图）：

我们把这张图斜着的边拉直（黑色部分），最左边的一列路径改成折线（红色部分），得到：

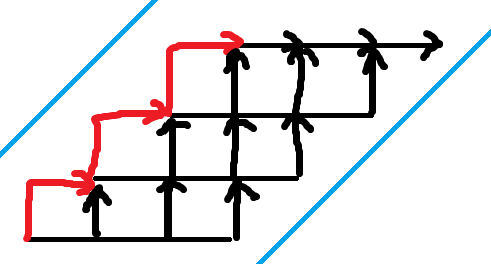
我们发现两条蓝线正好是 \(l_1,l_2\)，题目转化成从 \((0,0)\) 到 \((n + m + 1,m)\)（不理解终点为什么在这的可以可以手搓一下），不碰到 \(l_1,l_2\) 的方案数，用上文方法即可。

Code

#include <bits/stdc++.h>
using namespace std;

#define int long long
constexpr int maxn = 3000010, modd = 1000000007;

int n, m, fac[maxn], invfac[maxn], ans;

int ksm(int a, int b) { // 快速幂
	int ress = 1;
	while (b) {
		if (b & 1) ress = ress * a % modd;
		a = a * a % modd;
		b >>= 1;
	}
	return ress;
}

void init() { // 阶乘初始化，用来加速组合数
	fac[0] = invfac[0] = 1;
	for (int i = 1; i < maxn; i++) {
		fac[i] = fac[i - 1] * i % modd;
		invfac[i] = ksm(fac[i], modd - 2);
	}
	return ;
}

int C(int a, int b) { // 组合数
	return fac[a] * invfac[b] % modd * invfac[a - b] % modd;
}

void mirrorL1(int &x, int &y) { // 关于 l1 对称
	int t = x;
	x = y - 1;
	y = t + 1;
	return ;
}
void mirrorL2(int &x, int &y) { // 关于 l2 对称
	int t = x;
	x = y + m + 2;
	y = t - m - 2;
	return ;
}

void solveA(int nowx, int nowy) { // A, AB, ABA, ABAB 情况的计数
	int flag = 0;
	mirrorL1(nowx, nowy);
	while (nowx >= 0 && nowy >= 0) {
		if (!flag) ans = (ans - C(nowx + nowy, min(nowx, nowy))) % modd;
		else ans = (ans + C(nowx + nowy, min(nowx, nowy))) % modd;
		flag ^= 1;
		if (flag) {
			mirrorL2(nowx, nowy);
		} else {
			mirrorL1(nowx, nowy);
		}
	}
	return ;
}
void solveB(int nowx, int nowy) { // B, BA, BAB, BABA 情况的计数
	int flag = 1;
	mirrorL2(nowx, nowy);
	while (nowx >= 0 && nowy >= 0) {
		if (flag) ans = (ans - C(nowx + nowy, min(nowx, nowy))) % modd;
		else ans = (ans + C(nowx + nowy, min(nowx, nowy))) % modd;
		flag ^= 1;
		if (flag) {
			mirrorL2(nowx, nowy);
		} else {
			mirrorL1(nowx, nowy);
		}
	}
	return ;
}

signed main() {
	ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	
	cin >> n >> m;
	
	init();
	ans = C(n + n + m + 1, n) % modd; // 总方案
	solveA(n + m + 1, n);
	solveB(n + m + 1, n);
	
	cout << (ans % modd + modd) % modd << '\n';
	
	return 0;
}