P3644 [APIO2015] 巴邻旁之桥
困难
思路
看到数据范围有 \(k = 1\) 和 \(k = 2\) 所以先考虑较简单的 \(k = 1\)。
当 \(k = 1\) 时,若起点终点在同侧那么直接加,所以只要考虑起点终点不同侧的情况。由于正着走反着走都一样,所以可以都看作是有 \(A\) 到 \(B\)。如图示一个例子,其中 \(PQ\) 是一条可能的桥。
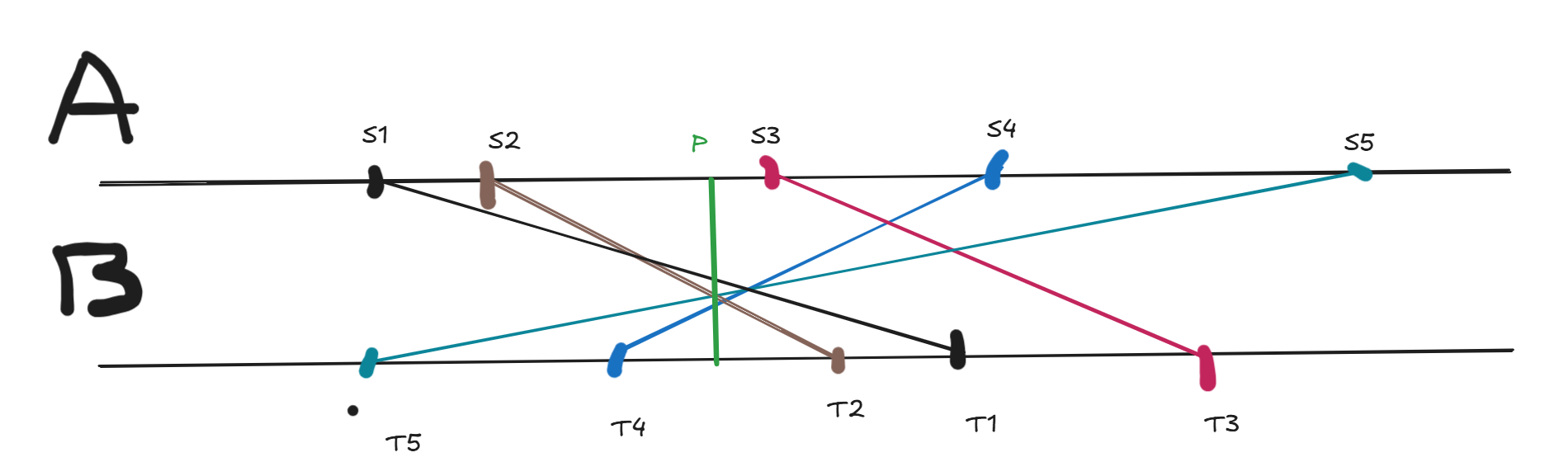
(制作工具 https://excalidraw.com/)
起点终点异则的路一定要经过桥,所以可以将每条路分成三段,\(s \to p\),桥上,¥q \to t$。其中桥长度是 \(1\),\(s \to p\) 长度是 \(abs(s - p)\),\(q \to t\) 长度是 \(abs(t - p)\)。由于我们要确定 \(p\) 使得所有路长度的和最小化,所以我们要使得 \(\sum_i^{m} (\mid s - p \mid + \mid t - p \mid + 1) = cnt + \sum_i^{m} (\mid s_i - p \mid + \mid t_i - p \mid)\) 最小化。我们可以把 \(s, t\) 看作是独立的,问题变成找一个 \(p\) 使得若干个点到 \(p\) 的距离的总和最小,这是一个经典结论,应取中位数,然后算距离和即可。
当 \(k = 2\) 时,如下图。
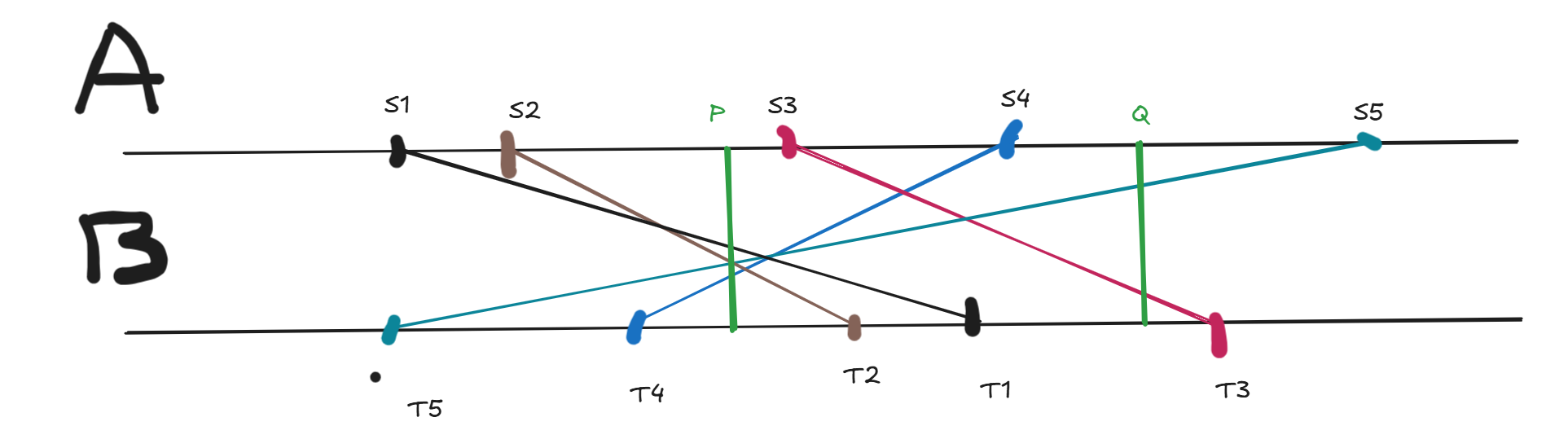
首先,建两条桥一定不劣于建一条桥,所以一定建两条桥。其次,桥的长度一定是 \(1\),且起点终点异侧的路一定要经过桥,所以可以不考虑桥,只考虑点之间的距离,最后加上异侧路的数量,则又如下图。

通过观察,我们可以发现当 \(frac{s + t}{2} < frac{p + q}{2}\) 时将走 \(p\),否则走 \(q\)。对于 \(p\) 和 \(q\) 同时在 \(s\) 和 \(t\) 间的情况,直接根据上述式子钦定是不劣的。我们将路按 \(s + t\) 排序,于是走 \(p\) 的是一个前缀,剩下后缀走 \(q\),我们枚举这个前缀,于是问题转化为两个 \(k = 1\),于是,用平衡树维护每个前缀后缀的中位数即可。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
using ll = long long;
const ll N = 2e6 + 5, INF = 1e18;
struct Node {
ll s, t;
};
struct TreapNode {
int sz, rk, l, r;
ll v, sum;
};
struct Cmp {
bool operator () (const Node &a, const Node &b) const {
return a.s + a.t < b.s + b.t;
}
};
int k, n, tot, rt1, rt2;
ll ans;
ll p[N], q[N];
TreapNode t[N];
vector<Node> a;
vector<ll> b;
void Up(int u) {
t[u].sz = t[t[u].l].sz + t[t[u].r].sz + 1;
t[u].sum = t[t[u].l].sum + t[t[u].r].sum + t[u].v;
return ;
}
void Split(int u, int &a, int &b, int v) {
if (!u) {
a = b = 0;
return ;
}
// Down(u);
if (t[u].v <= v) {
a = u;
Split(t[a].r, t[a].r, b, v);
} else {
b = u;
Split(t[b].l, a, t[b].l, v);
}
Up(u);
return ;
}
void Merge(int &u, int a, int b) {
if (!a || !b) {
u = a + b;
return ;
}
if (t[a].rk < t[b].rk) {
// Down(a);
u = a;
Merge(t[u].r, t[u].r, b);
} else {
// Down(b);
u = b;
Merge(t[u].l, a, t[u].l);
}
Up(u);
return ;
}
void Insert(int &rt, ll v) {
tot++;
t[tot].v = v;
t[tot].sz = 1;
t[tot].sum = v;
t[tot].rk = rand();
int a = 0, b = 0, c = tot;
Split(rt, a, b, v);
Merge(a, a, c);
Merge(rt, a, b);
return ;
}
ll Num(int u, int x) {
while (t[t[u].l].sz + 1 != x) {
if (t[t[u].l].sz + 1 < x) {
x -= t[t[u].l].sz + 1;
u = t[u].r;
} else {
u = t[u].l;
}
}
return t[u].v;
}
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
srand(time(0));
cin >> k >> n;
for (int i = 1, s, t; i <= n; i++) {
char p, q;
cin >> p >> s >> q >> t;
if (p != q) {
a.push_back({min(s, t), max(s, t)});
ans++;
} else {
ans += abs(s - t);
}
}
if (k == 1) {
b.push_back(0);
for (Node x : a) {
b.push_back(x.s);
b.push_back(x.t);
}
sort(b.begin(), b.end());
int cnt = (b.size() - 1) / 2, mid = b[cnt];
for (int i = 1; i < b.size(); i++) {
ans += abs(mid - b[i]);
}
} else {
a.push_back({-1, -1});
sort(a.begin(), a.end(), Cmp());
// cout << "---------------\n";
for (int i = 1; i < a.size(); i++) {
// cout << a[i].s << ' ' << a[i].t << '\n';
Insert(rt1, a[i].s), Insert(rt1, a[i].t);
ll mid = Num(rt1, i);
int x = 0, y = 0;
Split(rt1, x, y, mid);
p[i] = t[x].sz * mid - t[x].sum + t[y].sum - t[y].sz * mid;
// cout << t[x].sz << ' ' << t[x].sum << ' ' << t[y].sz << ' ' << t[y].sum << '\n';
Merge(rt1, x, y);
// cout << t[rt1].sz << ' ' << t[rt1].sum << ' ' << mid << '\n';
}
// cout << "---------------\n";
for (int i = a.size() - 1; i >= 1; i--) {
// cout << a[i].s << ' ' << a[i].t << '\n';
Insert(rt2, a[i].s), Insert(rt2, a[i].t);
ll mid = Num(rt2, a.size() - 1 - i + 1);
int x = 0, y = 0;
Split(rt2, x, y, mid);
q[i] = t[x].sz * mid - t[x].sum + t[y].sum - t[y].sz * mid;
Merge(rt2, x, y);
// cout << t[rt2].sz << ' ' << t[rt2].sum << ' ' << mid << '\n';
}
// cout << "---------------\n";
ll mn = INF;
for (int i = 0; i < a.size(); i++) {
// cout << p[i] << ' ' << q[i] << '\n';
mn = min(mn, p[i] + q[i + 1]);
}
ans += mn;
}
cout << ans;
return 0;
}
/*
思路
- 画图
- 推性质
- 手摸样例
- 换个角度
检查
- long long
- 多测要清空 Clear
- ios
- 各变量和下标
- 数据范围
- 上下界
- freopen
*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号