通过前序遍历（后序遍历）和中序遍历画出唯一的一棵二叉树

这里举一个例子：

一棵二叉树的中序遍历序列为：DGBAECHF，后序遍历序列为：GDBEHFCA，则前序遍历的序列是什么？

这一类题目主要以选择填空为主，有时候会作为解答题让我们画出二叉树。当然做这一类题目也有技巧，故介绍如下几种技巧。

1.三种遍历

中序遍历先访问左子树，再访问根节点，最后访问右子树。

前序遍历先访问根节点，再访问左子树，最后访问右子树。

后序遍历先访问左子树，再访问右子树，最后访问根节点。

2.判断根节点

如果要画出唯一一棵树，那么必须要前序遍历（后序遍历）和中序遍历，

前序遍历的第一个字母即为整棵树的根节点，后序遍历的最后一个字母即为整棵树的根节点。

然后再根据根节点在中序遍历中的位置，判断左子树和右子树。

2.选择题解题方法（特殊情况）

如果例题有了以下几个选项：A.ABDGCEFH   B.BACDFGHE   C.FCEAHBGD   D.GFEDCBA

显然D选项是闹着玩的不正确的，根据上面的方法，发现这一题的根节点为A，即左子树的元素有{BDG}，右子树的元素有{CEFH}。

 

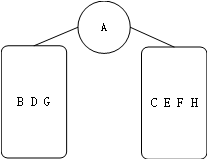
 很显然，根节点是A，那么前序遍历的第一个字母一定是A，答案即为A，当然这一种送分题也是比较少见。

一般来说，两个子树的元素有一边的数量比较少，在3-4个字母之间，应该从少的下手。

3.正常解题方法

刚刚我们已经分出了左右子树的元素，接下来我们从少的一边（左子树）下手。

对于左子树来讲，中序遍历为：DGB，后序遍历为：GDB。

那么这三个元素可以放置的位置如下：

 

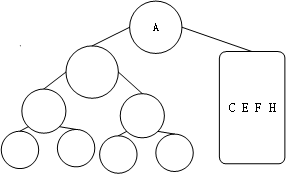
 接下来，我们需要思维转变，我们创建有这三个元素组成的一颗新的树。

根据上面的方法，我们可以知道这一颗树的根节点为B，左子树的元素有{AB}，右子树的元素有{}，即为空集。

接下来再重复上面的方法，把D理解为新的子树的根节点，那么左子树的元素为{}，即为空集，右子树的元素为{G}。

根据上面的结论画出图像：

 

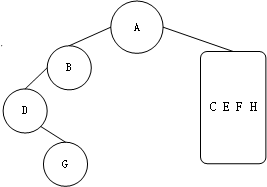
 右侧同理，画出图像：

 

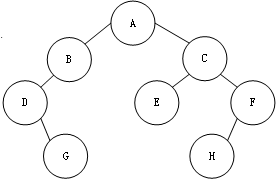
 故前序遍历为：ABDGCEFH。

最后放上雪之下