郑州地铁路线规划系统1.1 --计应193吕志江
一计划、
目标要实现郑州地铁路线规划。输入出发点和终点。要能够自动规划出最短的路线。
二开发、
1.需求分析
作为一名大学生。我想要在周末乘地铁去郑州其他地方游玩。我需要知道如何规划最短路线。
这里需要实现几个功能:
- 将郑州地铁路线录入
- 能够接受用户输入的出发点和终点
- 要能够自动生成最短路线
2生成设计文档
3.设计复审
4.代码规范
按照开发工具(eclipse)对JAVA的规范要求处理
5.具体设计
上一次的开发实现了MVP。那么这次的开发要对MVP进行拓展,先将郑州地铁路线转换成代码,再将其与MVP进行对接、拓展。
在开发过程中发现,MVP的逆向查找功能会报错,不能正常运行。所以着手对输出最短路线算法进行优化。原算法需要建立二维数组,纵向截取,整理答案。现算法思想为:只看最后一次的上级节点,然后对其进行分析,在最终一次的上级节点数组中,给定终点,通过查表就可以知道,终点的上一级节点是哪个节点,然后再找到终点的上一级节点的上一级节点。从而找到完整的路径。在保存过程中发现,如果简单地以数组保存的话,一是不知道数组长度该设为多少,二是保存的路线是由终点往上倒着找的。所以保存的是反过来的路径。基于此,想到使用双向链表,网上查资料时发现使用双向链表的话,也许会更加复杂。于是转而使用了JAVA中的List对象。该对象很好的解决了数组长度的问题。并且其中的add方法也能够以栈的形式保存元素,也解决了路线是反着保存的问题。现在路线仍然是反着保存,但其有栈的特性,读取时可以先入后出。完美的解决了路线存储的问题。
那么这样一来,前期所做的二维数组存储路线、纵向截取这一算法就可以被替换掉了。其中的二维数组可以改为一维数组。效率也得到了提高。
下一步就可以改变图,将郑州地铁数据进行录入。
首先将原来的char类型全部改为String类型。使其功能性更强。
将郑州地铁数据进行录入。郑州地铁站点很多。如果手动录入则工作量非常大,猜想能否进行自动录入。自动生成对应的图。
以一号线为例。通过观察发现,邻接矩阵的第一行的值,只有第二个值为1,最后一行的值,只有倒数第二个值为1。其他的行,值为1的点与行数的关系为n-1与n+1的值为1(n为行数)。其他的值都为N。那么由此构建模型,代码实现,即可以只写一个关于线路
的字符串数组,就可以得到一个关于此数组的邻接矩阵。(这里通过传入行号与字符串书组的长度,在for循环内循环调用这个函数。就可以初始化生成一个关于某一条路线的邻接矩阵)
public static int [] fuzhi(int n,int jiedianshu){
final int N = 65535 ;
int [] z = new int [jiedianshu];
Arrays.fill(z , N);
if(n == 0 || n == jiedianshu-1) {
if(n==0) {
//Arrays.fill(z , 1 , 2 , 1);
z[1]=1;
}else {
//Arrays.fill(z, jiedianshu-2, jiedianshu-1, 1);
z[jiedianshu-2]=1;
}
}else {
z[n-1] = 1;
z[n+1] = 1;
}
return z;
}
那么有了一条线的临界矩阵。接下来要考虑的是如何将多条线路合并成为一个邻接矩阵。这个问题。经过思考。将各个临界矩阵按下图的方式合并即可。再将换乘点对应改写即可。
|
一号线的邻接矩阵 |
|
|
|
|
二号线的邻接矩阵 |
|
|
|
|
三号线的邻接矩阵 |
主要的思考方向就在于换乘点能否通过代码实现?暂时得出的结论是不能,只能通过手动调整,修改数据。在此基础上得出了上述拼接矩阵的想法。
代码实现也很简单。
实现后对程序进行调试,却屡屡出错:
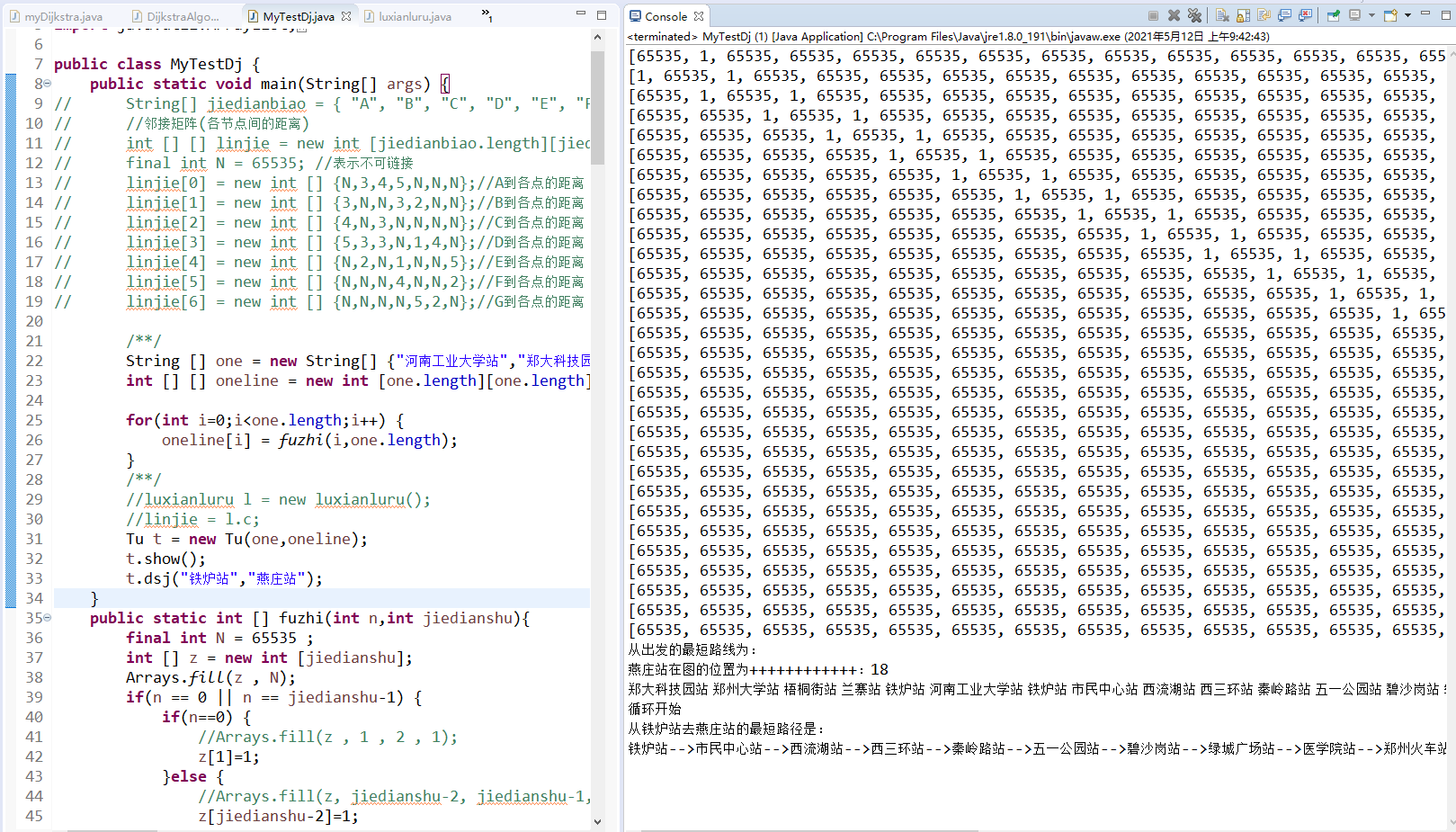
图示为一号线通车。
加入二号线后:

这三个紫荆山,是人民路站,东大街站和燕庄站的前驱节点。而当查找最短路径时却变成了紫荆山站的前驱节点。
为什么从二号线开始跨到一号线就出错?一号线跨二号线不报错的呀
二号线单线不出错。但是二号线单线跨紫荆山站就出错。
将一二号线合并后的数组中。紫荆山站出现了两次。这是导致错误的原因。这两个站点在图中本就是一个站点。不应该画成两个站点。画成两个站点后,在字符串数组中查找指定字符串的下标的方法就出错了。因为有两个同名的字符串。在查找时不能正常执行。
这样修改的话。将合并后的数组删除掉后面的紫荆山站。这样对应生成的邻接矩阵也应该修改。生成的紫荆山站的入度和出度都为2,现在应该改成4,加入黄河路站和东大街站。
这样,一二号线就通车了。
完成以上步骤,一二号线就通车了。不难总结出实现地铁通车的办法:建立地铁字符串数组,将两条线合并字符串数组,去掉重复的字符串。在生成邻接矩阵后修改换乘点的入度和出度。好像有些麻烦。如果要把这些交给程序去完成。那就需要将以上步骤合并。在去掉重复的字符串的同时,得到重复字符串的下标,这样就知道邻接矩阵该修改的地方在哪里了。所以需要合并字符串数组的函数返回一个下标。这样以来,这个函数不仅需要返回一个合并好的字符串,还需要返回一个下标。这样考虑把下标和字符串定义为一个对象。再想想,后期这个函数需要做的是将一二号线合并,合并后的线暂称为allline,然后再将allline和三号线合并,这个时候就产生了问题,allline和三号线一定只有一个换乘点吗?返回值一定只有一个下标吗?
如何实现多线路逐步叠加,最终形成完整图?叠加后各换乘点的度如何自动改变?如何将B矩阵,去掉与A矩阵相同的节点,以便于AB矩阵合并,合并后的矩阵就是完美矩阵。也即将AB矩阵相同的节点只保留一个。
这些问题通过一系列方法进行实现了。将两个矩阵合并,并且过程中要将重复的点去除,字符串数组也要将重复的点去除。邻接矩阵要去掉重复的点,这里去除重复的点不关注去除哪一个点,而只关注去除几个。然后根据长度自动生成新的邻接矩阵进行合并。合并之后要修改重复点的度。这里经过测试得出了一个方法:
public static void xiugaidu(int [] [] line,int a, int b) {
System.out.println("这里对度进行修改:此时修改的节点为:"+ b);
line[a][b]=1;
line[b][a]=1;
line[a][b-1]=1;
line[b-1][a]=1;
System.out.println("------------------这里是修改度后的邻接矩阵--------------");
for(int [] link : line) {
System.out.println(Arrays.toString(link));
}
}
只需要传入需要修改的邻接矩阵,和两个下标即可。这两个下标代表的就是重复点的下标。关于这个下标的获取,要从合并矩阵时获取到。在合并矩阵的时候查找到重复点的下标,并保存起来,这里有可能不止一个重复的点,所以使用List集合进行保存。
6.具体编码
最终形成的代码如下:
package text;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Iterator;
import java.util.List;
public class MyTestDj {
public static void main(String[] args) {
/**/
String [] one = new String[] {"河南工业大学站","郑大科技园站","郑州大学站","梧桐街站","兰寨站","铁炉站","市民中心站","西流湖站","西三环站","秦岭路站","五一公园站","碧沙岗站","绿城广场站","医学院站","郑州火车站","二七广场站","人民路站","紫荆山站","燕庄站","民航路站","会展中心站","黄河南路站","农业南路站","东风南路站","郑州东站","博学路站","市体育中心站","龙子湖站","文苑北路站","河南大学新区站"};
//String [] onefour = new String[] {"铁炉站","市委党校","奥体中心"};
String [] two = new String[] {"贾河","惠济区政府","毛庄","黄河迎宾馆","金洼","金达路","刘庄","柳林","沙门","北三环","东风路","关虎屯","黄河路","紫荆山站","东大街","陇海东路","二里岗","南五里堡","花寨","南三环","站马屯","南四环"};
//String [] cj = new String[] {"南四环","十八里河","沙窝李","双湖大道","小乔","华南城西","华南城","华南城东","孟庄","港区北","康平湖","兰河公园","恩平湖","综合保税区","新郑机场"};
// String [] one = new String[] {"郑州火车站","二七广场站","人民路站","紫荆山站","燕庄站"};
// String [] two = new String[] {"关虎屯","黄河路","紫荆山站","东大街","陇海东路"};
// String [] allline = new String [] {"郑州火车站","二七广场站","人民路站","紫荆山站","燕庄站","关虎屯","黄河路","东大街","陇海东路"};
int [] [] oneline = new int [one.length][one.length];
int [] [] twoline = new int [two.length][two.length];//定义二号线的邻接矩阵
//int [] [] onefourline = new int [onefour.length][onefour.length];//定义十四号线的邻接矩阵
for(int i=0;i<one.length;i++) {
oneline[i] = fuzhi(i,one.length);
}
//为二号线的临界矩阵赋值
for(int i=0;i<two.length;i++) {
twoline[i] = fuzhi(i,two.length);
}
// for(int i =0;i<onefour.length;i++) {
// onefourline[i] = fuzhi(i,onefour.length);
// }
/*int [] [] c = hebing(oneline,twoline);//组合一号线,二号线的邻接矩阵
System.out.println("c.length:="+c.length);
//下面四行是对于紫荆山站的入度出度修改
c[17][43]=1;
c[43][17]=1;
c[17][42]=1;
c[42][17]=1;*/
//xiugaidu(c,before,after);
String [] all = shengchengshuzu(one,two);//生成合并后的新数组
int [] [] allline=shengchengjuzhen(one,two,oneline,twoline);//生成一二号线的合并邻接矩阵
//这里加入十四号线
//all = shengchengshuzu(all,two);
//System.out.println("onefourline.length=" + onefourline.length);
//allline = shengchengjuzhen(all,two,allline,twoline);
System.out.println("---------------------------------------------");
// System.out.println("allline[][]的参数长度为:"+allline[0].length);
// System.out.println("c[][]的参数长度为:"+c[0].length);
//hebing(one,two);
Tu t = new Tu(all,allline);
t.show();
t.dsj("河南工业大学站", "毛庄");
}
public static int [] fuzhi(int n,int jiedianshu){
final int N = 65535 ;
int [] z = new int [jiedianshu];
Arrays.fill(z , N);
if(n == 0 || n == jiedianshu-1) {
if(n==0) {
//Arrays.fill(z , 1 , 2 , 1);
z[1]=1;
}else {
//Arrays.fill(z, jiedianshu-2, jiedianshu-1, 1);
z[jiedianshu-2]=1;
}
}else {
z[n-1] = 1;
z[n+1] = 1;
}
return z;
}
public static int [][] hebing(int [][] a ,int [][] b) {
int clin=a.length + b.length;
System.out.println("合并后的矩阵的长度应该是是"+ a.length + "+" + b.length + " = "+clin);
final int N = 65535 ;
int[][] c = new int[clin][clin];
//初始化所有值为N
for(int [] s :c) {
Arrays.fill(s, N);
}
//第一个二维数组一个值一个值的输入。第二个二维数组一个值一个值的输入
for(int i=0;i<a.length;i++) {
for(int j=0;j<a.length;j++) {
c[i][j] = a[i][j];
}
}
for(int q=0;q<b.length;q++) {
for(int j=0;j<b.length;j++) {
c[a.length+q][a.length+j] = b[q][j];
//System.out.print(b[q][j]+" +");
}
// System.out.println();
// System.out.println("修改的是"+(a.length+q)+":"+(a.length+q)+"位置的值"+c[a.length+q][a.length]);
// System.out.println("这是第"+q+"次运行");
}
System.out.println("实际合并后的长度是"+c.length);
return c;
}
//合并两个字符串数组,返回一个字符串数组
public static jieguodian hebing(String[] a, String[] b) {
System.out.println("合并方法调用了***************************");
System.out.println("传入的第一个数组的最后一个值为:"+a[a.length-1]);
jieguodian j = new jieguodian();
List<String> lineList= new ArrayList<String>();
int len = a.length + b.length;// 这个链表最多有这么多的元素
//这个算法稍复杂,将两个数组合并,并且去掉重复元素。难点在第二个数组录入时发现重复元素怎么办。 关在在于两个指针指向要发生变化,于是做差。改变成差值的变化。
for (int i = 0; i < len;i++) {
if (i < a.length) {// 当i仍在a的范围内就赋值给h
lineList.add(a[i]);
} else {
//System.out.println("此时集合中的最后一个值为:"+lineList.get(lineList.size()-1));
if (!Arrays.asList(a).contains(b[i - a.length])) {// 如果a数组中不包含b[i-a.length]元素
lineList.add(b[i - a.length]) ;
} else {
System.out.println("发现重复元素:"+b[i - a.length]);
//System.out.println(new Tu().chazhao(b[i - a.length],a));
j.setBefore(new Tu().chazhao(b[i - a.length],a));
j.setAfter(i);
//System.out.println("before=" + new Tu().chazhao(b[i - a.length],a));
//System.out.println("after="+i);
//System.out.println("下一个元素为:"+b[i+1 - a.length]);
//System.out.println("下下一个元素为:"+b[i+2 - a.length]);
}
}
}
String[] h = lineList.toArray(new String[lineList.size()]); //将链表转换为字符串数组
j.setArr(h);
System.out.print("这里是合并字符串数组的结果:结果为:");
for(int i = 0 ;i<j.getArr().length;i++) {
System.out.print(i+ j.getArr()[i] + ", ");
}
return j;
}
public static void xiugaidu(int [] [] line,int a, int b) {
System.out.println("这里对度进行修改:此时修改的节点为:"+ b);
line[a][b]=1;
line[b][a]=1;
line[a][b-1]=1;
line[b-1][a]=1;
System.out.println("------------------这里是修改度后的邻接矩阵--------------");
for(int [] link : line) {
System.out.println(Arrays.toString(link));
}
}
public static int [] [] shengchengjuzhen(String [] a,String [] b,int [][]c,int [][]d){
jieguodian j = new jieguodian();
j = hebing(a , b);
int clin=a.length + b.length - j.getAfter().size();
System.out.println();
System.out.println("clin = " + (a.length) + " + " + (b.length) + " - " + j.getAfter().size() + " = " + clin);
final int N = 65535 ;
int[][] f = new int[clin][clin];
//初始化所有值为N
for(int [] s :f) {
Arrays.fill(s, N);
}
//第一个二维数组一个值一个值的输入。第二个二维数组一个值一个值的输入
for(int i=0;i<c.length;i++) {
for(int y=0;y<c.length;y++) {
f[i][y] = c[i][y];
}
}
// System.out.println();
// System.out.println("++++++++++++++++++++++++修改前的d+++++++++++++++");
// System.out.println("此时的长度为:"+d.length);
// for(int [] link : d) {
// System.out.println(Arrays.toString(link));
// }
// System.out.println((j.getBefore().get(0)));
//去掉D矩阵中重复的值:
d = shanchushuzu(j.getAfter().get(0),d);
// System.out.println();
// System.out.println("++++++++++++++++++++++++修改后的d+++++++++++++++");
// System.out.println("此时的长度为:"+d.length);
// for(int [] link : d) {
// System.out.println(Arrays.toString(link));
// }
for(int q=0;q<d.length;q++) {
for(int z=0;z<d.length;z++) {
f[c.length+q][c.length+z] = d[q][z];//这里不确定是不是+1
//System.out.print(b[q][j]+" +");
}
}
System.out.println();
System.out.println("++++++++++++++++++++++++for循环后的f+++++++++++++++");
System.out.println("此时的长度为:"+f.length);
for(int [] link : f) {
System.out.println(Arrays.toString(link));
}
System.out.println("finally合并后的矩阵的长度是:"+f.length);
//更改度
for(int i = 0;i<j.getBefore().size();i++) {
System.out.println("本次是第" + i + "次修改度");
System.out.println("修改的度为:" + "(" + j.getBefore().get(i)+ ","+j.getAfter().get(i) + ")");
//System.out.println("代表的节点为:" + f[j.getBefore().get(i)][j.getAfter().get(i)]);
xiugaidu(f,j.getBefore().get(i),j.getAfter().get(i));
}
return f;
}
public static int [] [] shanchushuzu(int x, int[][]y){
System.out.println("y[0].length - 1="+ (y[0].length - 1));
System.out.println("有点奇怪");
int[][] z = new int[y[0].length - 1][y[0].length - 1];
System.out.println("z.length="+z.length);
for(int [] s :z) {
Arrays.fill(s, 65535);
}
for(int i =0;i<z.length;i++) {
z[i] = fuzhi(i,z.length);
}
return z;
}
public static String [] shengchengshuzu(String []a, String[]b) {
jieguodian j = new jieguodian();
j = hebing(a , b);
int o = 0;
System.out.println("这里是方法内部:");
System.out.println("j的生成的数组是:");
for(String i : j.getArr()) {
System.out.println(o+i);
o++;
}
return j.getArr();
}
}
class Tu {
private String [] jiedianbiao;//定义节点表
private int [][] linjie;//定义邻接矩阵
private int [] fangwen;//定义访问与否
private int [] juli;//定义距离
private int [] shangji;//定义上级节点
private String [] luxian;//定义路线
//定义构造器
public Tu() {};
public Tu(String[] jiedianbiao,int [][] linjie) {
this.jiedianbiao = jiedianbiao;
this.linjie = linjie;
luxian= new String[jiedianbiao.length];
}
//查看邻接图
public void show() {
for(int [] link : linjie) {
System.out.println(Arrays.toString(link));
}
}
//实现迪杰斯特拉算法
public void dsj(String start, String end){
int s = chazhao(start,jiedianbiao);
first(s,chazhao(end,jiedianbiao));
update(s);
for(int j = 1; j <jiedianbiao.length; j++) {
s = updateFangwen();// 选择并返回新的访问顶点
update(s); // 更新index顶点到周围顶点的距离和前驱顶点
}
zuiduanluxian(start, jiedianbiao, end);
}
//输出最短路径
public void zuiduanluxian(String start, String[] tu, String end) {
String[] op = tu;
int index1 = chazhao(end, tu);
System.out.println("从出发的最短路线为:");
System.out.println(end + "在图的位置为++++++++++++:" + index1);
int k = 0;
int y = 0;
//luxian[17]="黄河路";
for(String i : luxian) {
System.out.print(k++ + i + " ");
}
System.out.println();
System.out.println("节点表");
for(String i : jiedianbiao) {
System.out.print(y++ + i + " ");
}
System.out.println();
//这里作更改,将原本纵向截路线图改为截最后一组路线图,整个输出最短路径的算法被更改。下面被注释的是原来的代码
/*for (int i = 0; i < tu.length - 1; i++) {
//System.out.println(i + "==>" + luxian[i][index1]);
op[i] = luxian[i][index1];
}
List<Character> list = new ArrayList<>();
for (int h = 0; h < op.length - 1; h++) {
if (!list.contains(op[h])) {
list.add(op[h]);
}
}
System.out.println("从" + start + "去" + end + "的最短路径是:");
System.out.print(start + "-->");
for (char i : list) {
if (i == start || i == end) {}
else {
System.out.print(i + "-->");
}
}
System.out.print(end);*/
op = luxian;
List<String> xxxx=new ArrayList<>();
//经过分析想使用双向链表,先做小测试,随后再重构
String mid = end;
System.out.println("循环开始:mid=="+ mid);
System.out.println("测试搜索方法");
System.out.println("紫荆山站 + " + sousuo(op,"紫荆山站"));
for(int i = 0;i<=100;i++) {
if(start==sousuo(op,mid)) {
break;
}else {
mid=sousuo(op,mid);
xxxx.add(0, mid);//每次都将新得的值赋给0位置
}
}
System.out.println("xxxx的长度为:"+xxxx.size());
System.out.println("从" + start + "去" + end + "的最短路径是:");
System.out.print(start + "-->");
for(String i: xxxx) {
System.out.print(i + "-->");
}
System.out.print(end);
}
//初始化节点数组
public void first(int index, int end) {
//定义初始长度
this.fangwen = new int[jiedianbiao.length];
this.juli = new int[jiedianbiao.length];
this.shangji = new int[jiedianbiao.length];
//赋初始值
Arrays.fill(juli, 65535);
//更改起点的属性
fangwen[index] = 1;
juli[index] = 0;
}
//更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
public void update(int index) {
int len = 0;
//根据遍历我们的邻接矩阵的 linjie[index]行
for(int j = 0; j < linjie[index].length; j++) {
// len 含义是 : 出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
len = juli[index] + linjie[index][j];
// 如果j顶点没有被访问过,并且 len 小于出发顶点到j顶点的距离,就需要更新
if(!in(j) && len < juli[j]) {
//System.out.println("jishu=="+jishu);
//System.out.println("luxian[jishu].length==" + luxian[jishu].length);
luxian = updateShangji(j, index); //更新j顶点的前驱为index顶点
updateDis(j, len); //更新出发顶点到j顶点的距离
}
}
}
/**
* 功能: 更新jiedian这个顶点的前驱顶设置点为index顶点
* @param jiedian
* @param index
*/
public String[] updateShangji(int jiedian,int index) {
shangji[jiedian] = index;
//定义记录每一次的前置节点
String [] hangluxian = new String[jiedianbiao.length];
for(int i = 0;i<shangji.length;i++) {
hangluxian[i] = jiedianbiao[shangji[i]];
}
return hangluxian;
}
//判断是否访问过该节点
public boolean in(int index) {
return fangwen[index] == 1;
}
/**
* 继续选择并返回新的访问顶点, 比如这里的G 完后,就是 A点作为新的访问顶点(注意不是出发顶点)
* @return
*/
public int updateFangwen() {
int min = 65535, index = 0;
for(int i = 0; i < fangwen.length; i++) {
if(fangwen[i] == 0 && juli[i] < min ) {
min = juli[i];
index = i;
}
}
//更新 index 顶点被访问过
fangwen[index] = 1;
return index;
}
/**
* 功能: 更新出发顶点到index顶点的距离
* @param index
* @param len
*/
public void updateDis(int index, int len) {
juli[index] = len;
}
//用来将字符串转化成数组下标
public int chazhao(String a,String[] arr) {
int x = -1;
for(int i=0;i<arr.length;i++) {
if(a==arr[i]) {
x=i;
break;
}
}
return x;
}
//该方法用来处理最后的上级节点图。调用一次,就能知道@mubiao的上级节点是谁。通过反复调用此方法,便可以查出明确的路径来。
public String sousuo(String [] tu , String mubiao) {
String x = " ";
//System.out.println(tu);
System.out.println("传入的目标为"+mubiao);
int u = chazhao(mubiao,jiedianbiao);
System.out.println("u的值为:"+u);
if(u != -1) {
x = tu[u];
}
return x;
}
}
package text;
import java.util.ArrayList;
import java.util.List;
public class jieguodian {
private List<Integer> before;
private List<Integer> after;
private String [] arr;
jieguodian(){
List<Integer> bef = new ArrayList<Integer>();
List<Integer> aft = new ArrayList<Integer>();
this.after=aft;
this.before=bef;
}
public List<Integer> getBefore() {
return before;
}
public void setBefore(int before) {
this.before.add(before);
}
public List<Integer> getAfter() {
return after;
}
public void setAfter(int after) {
this.after.add(after);
}
public String[] getArr() {
return arr;
}
public void setArr(String[] arr) {
this.arr = arr;
}
}
截至发布博客前,此版本目前能实现一二号线的互通。在此基础上计划完善合并字符串和合并邻接矩阵的方法。使其能够拓展到自动将十四号线,三号线、城郊线录入链接。但在后续的调试中出现了异常。开发遇到了瓶颈。
总结:
此项目非常具有挑战性。以我个人的知识储备来说还有些困难。主要是算法思路上的困难。不太容易想得到解决办法。 最核心的迪杰斯特拉算法是新学的。然后在那个基础上不断拓展更新。原计划这个项目要更新到除五号线外所有线全部录入通车。因为五号线涉及到一个拆环的问题。打算留在下一个版本再进行突破。但目前的开发出现了问题。这个项目开发了半个多月左右。一半时间实现了从MVP到一二号线通车。另一半时间花到了如何将其他路线链接进来。每天的工作就是:改昨天出现的BUG,然后再写一个BUG明天改。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号