数据结构——查找
| 这个作业属于哪个班级 | C语言--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 骆锟宏 |
0.PTA得分截图
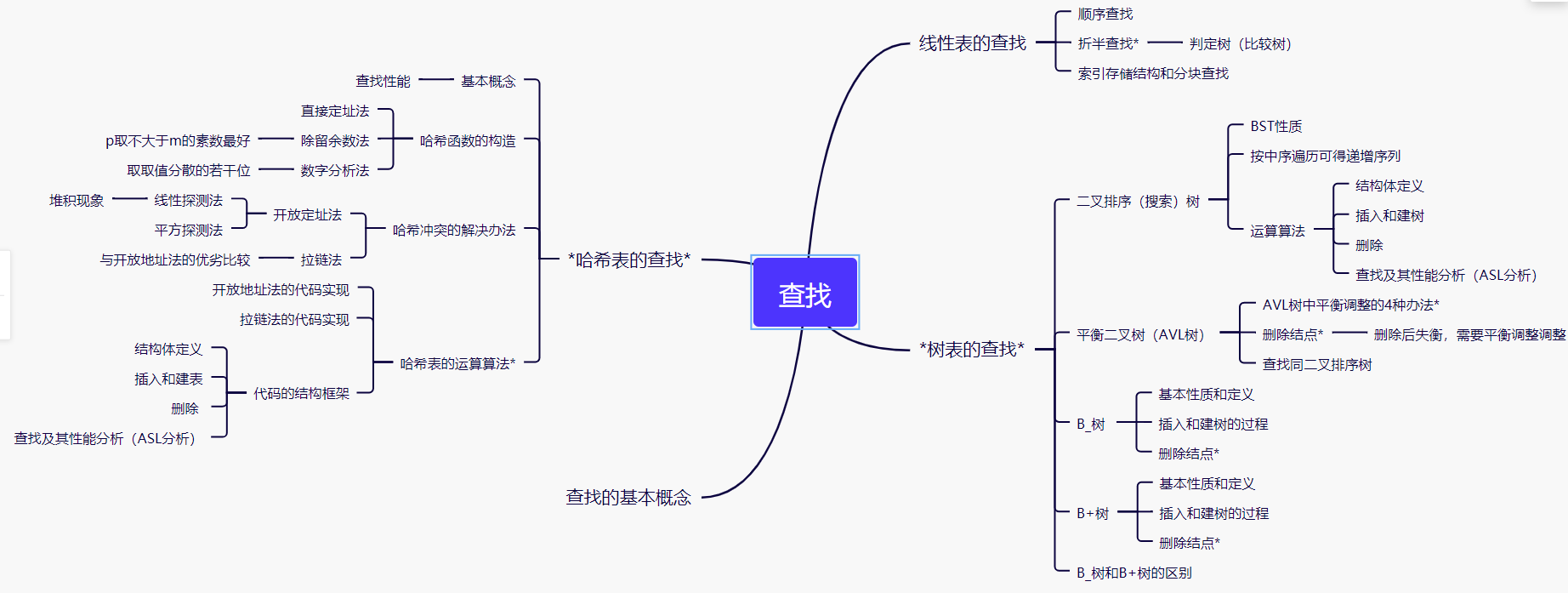
查找的整体的思维导图如下:
1.本周学习总结(0-5分)
1.1 查找的性能指标
- ASL成功:指的就是假设对所有可能的查找成功的情况的概率是相同的情况下,找到指定数据所需要进行比较的次数的和的平均值。
- ASL不成功:指的就是假设对所有可能的查找不成功的情况的概率是相同的情况下,判断找不到指定数据为止,所需要进行比较的次数的和的平均值。
- 比较次数:就是一轮查找中,待查找对象和其他已经存在的值进行比较的次数。(比较指出现了比较表达式)
- 移动次数:指的是元素从一个位置移动到另一个位置所需要与其他元素交换位置的次数,每次与一个元素交换一次位置,成为移动一次。
- 时间复杂度:指的是,执行查找算法所需要执行的核心语句的次数和问题规模之间的函数关系的最大数量级,用O来表示这种当问题规模n趋近于无穷的时候的渐进关系。直观的理解就是用来衡量算法的运行效率的一个量。
1.2 静态查找
- 顺序查找
- 成功ASL:顺序查找查找成功的次数为(n+1)/2
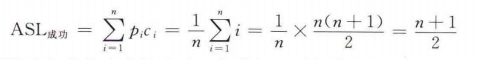
- 不成功ASL:由于顺序查找每次查找不成功都需要遍历整个线性表,所以不成功的ASL为表长n。
- 成功ASL:顺序查找查找成功的次数为(n+1)/2
- 二分查找
二分查找的关键在于构造出比较(判定)树。
以教材上的例题为例:
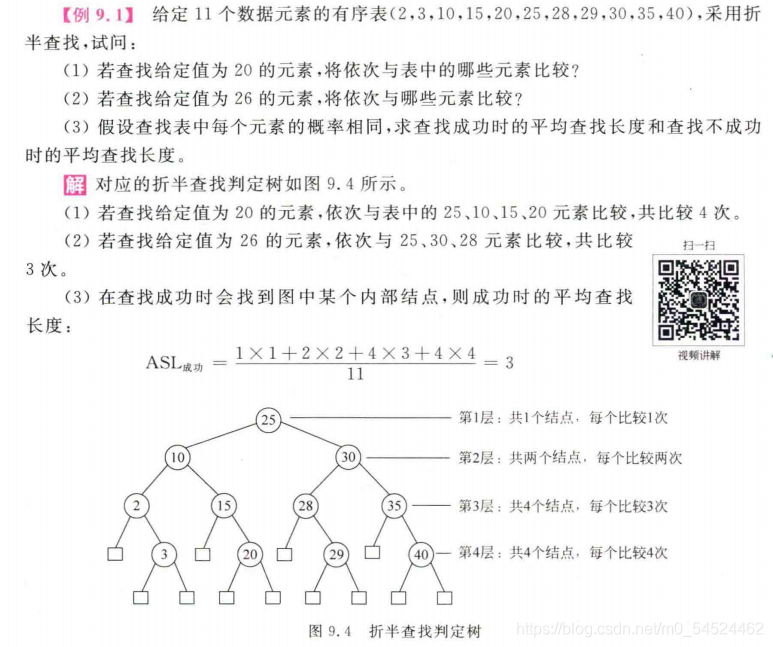

- 可以知道,如果按递归的代码来看的话,比较树的层数对应的是递归的深度,而结点的关键字的值,刚好是每个序列的中间下标所对应的元素。(mid = (left+right)/2)
- 查找成功的ASL的分子是这个序列所含有的元素的个数,分母是查找到对应的元素所需要进行的比较的次数的累加。
- 查找不成功的ASL的分母是构建出来的比较树中,补足的外部结点的个数(也即是空结点的个数),而分子则是查找到NULL结点所需要比较的次数的累加,特别地,空结点并没有进行比较,这个地方的比较次数是不进行计算的。
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
- 结合一组数据介绍构建过程
- 二叉搜索树的ASL成功和不成功的计算方法。
以课堂派的这道题为例:

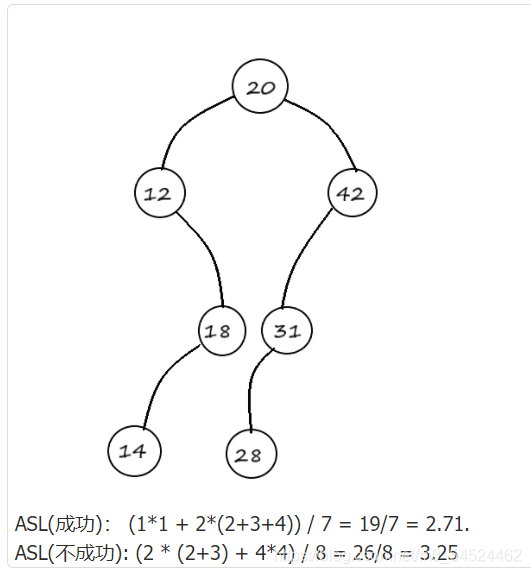
构建:以序列的第一个给出的元素作为根节点,然后依次扫描剩下的元素,比根节点大的放入右子树
比根节点小的放入左子树,一层一层递归下去,直到完全构建完成为止。
ASL的计算方法:和折半查找的比较树的判定方法一致,这里不再赘述。 - 如何在二叉搜索树做插入、删除。
-
插入的做法:
- 与当前节点不断比较;
- 如果比当前结点的值小,就往当前结点的左子树寻找插入的位置;
- 如果比当前结点的值大,就往当前结点的右子树寻找插入的位置;
- 只到找到空结点的时候,新建一个结点,借助递归返回上级的结点,融入整颗树中。
以下是补充书本的详细的解释:

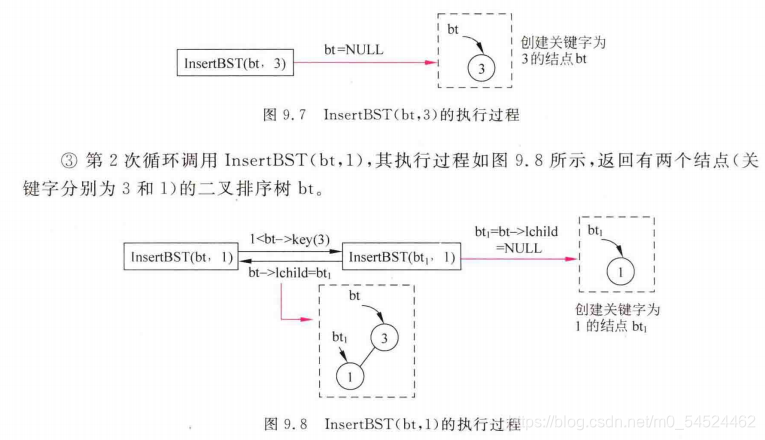
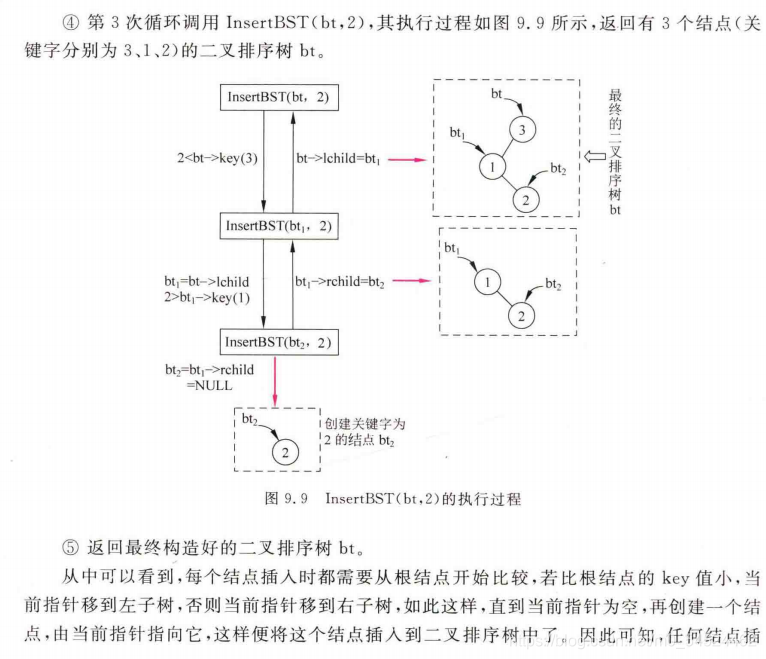

-
删除的做法:
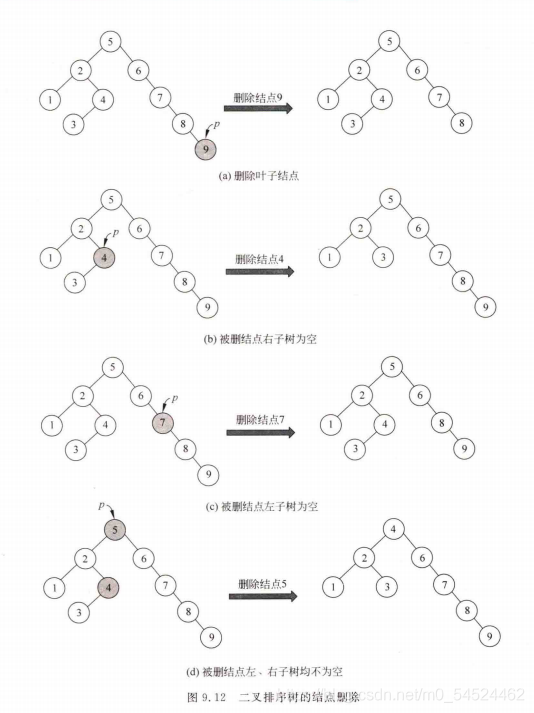
-
叶子结点直接删除;
-
被删结点左子树为空,右子树不为空,那就直接把右子树接上来;
-
被删结点右子树为空,左子树不为空,那就直接把左子树接上来;
-
被删结点左右子树都不为空去左子树找最左的结点,或者去右子树找最右的结点来充当新的结点。
1.3.2 如何构建二叉搜索树(代码)
- 如何构建、插入、删除及代码。
- 插入的代码:
BinTree Insert(BinTree BST, ElementType X)
{
//当发现当前结点是空结点时,便是插入的时刻了
if (BST == NULL)
{
BST = (BinTree)malloc(sizeof(BinTree));
BST->Data = X;
BST->Left = BST->Right = NULL;
return BST;
}
else if (BST->Data == X)
{
return BST;
}
else if(BST->Data > X)
{
//别忘了插入后的结点该返回给谁
BST->Left = Insert(BST->Left, X);
}
else//BST->Data < X
{
BST->Right = Insert(BST->Right, X);
}
//最后建完树应该把建完的整棵树返回回去。
return BST;
}
- 构建就是在插入的基础上,将整个表的所有数据,通过增加一个循环来多次调用插入而已。
- 删除的代码:
1. 递归的出口是访问到空结点,因为采用递归来进行删除的话,本质上也是先进行查找,然后找到了再删除,找不到就没办法删除,这算递归的出口。
2. 然后就是查找的情况的分类,主要分为三类,当X的值比当前结点的值更大的时候,就往右子树查找,反之往左子树查找,最后剩下的就是找到了的情况。
3. 找到的情况还得根据结点所带有的孩子的情况来进行讨论,没有孩子的话直接删,有一个孩子的话,就直接让它的孩子接替它的位置,然后删除它本身。两个孩子都有的话,可以去找左子树中最大的结点或者右子树中最小的结点来代替当前的结点,并删除最值结点。
BinTree Delete(BinTree BST, ElementType X)
{
if (BST == NULL)//树空没得删 / 找不到的递归出口
{
printf("Not Found\n");
return BST;
}
if (X < BST->Data)//递归查找左子树
{
BST->Left = Delete(BST->Left, X);
}
else if (X > BST->Data)//递归查找右子树
{
BST->Right = Delete(BST->Right, X);
}
else//找到了
{
/*
BinTree Keep;
//左右子树都为空的叶子结点的情况,处理方法同任一子树为空的情况。
if (BST->Left == NULL)//左子树为空
{
Keep = BST;
BST = BST->Right;
free(Keep);
}
else if (BST->Right == NULL)//右子树为空
{
Keep = BST;
BST = BST->Left;
free(Keep);
}
else//当前要删的结点左右子树都存在。
{
BinTree LeftMax;
LeftMax = FindMax(BST->Left);//查找左子树最右的结点。
BST->Data = LeftMax->Data;
//下面这一句代码很有水平。
BST->Left = Delete(BST->Left, LeftMax->Data);
//找的是左子树的最大结点,那删的也得是左子树上的那个最大结点,
//删完之后的那棵左子树还得返回回来到它在我当下根结点所在的左子树的位置上。
}
*/
//中间这部分代码还可以优化,如下:
BinTree Keep;
if (BST->Left != NULL && BST->Right != NULL)//当前要删的结点左右子树都存在。
{
BinTree LeftMax;
LeftMax = FindMax(BST->Left);//查找左子树最右的结点。
BST->Data = LeftMax->Data;//替代关键字
BST->Left = Delete(BST->Left, LeftMax->Data);//在左子树上删除最大结点。
}
else
{
Keep = BST;
if (BST->Left == NULL)//左子树为空
{
BST = BST->Right;
}
else if (BST->Right == NULL)//右子树为空
{
BST = BST->Left;
}
free(Keep);
}
}
return BST;
}
- 分析代码的时间复杂度
- 由于采用递归方法来写删除操作的本质还是查找,查找得到就删除,找不到就退出,针对两个孩子结点都存在的情况,也只不过是对左子树或者右子树进行一个最值的查找而已,所以该代码的时间复杂度同查找的时间复杂度,为O(logn).
- 这里没有进行定量分析,待拓展和补充。
- 为什么要用递归实现插入、删除?递归优势体现在代码哪里?
- 代码量减少了很多,减少了线性讨论的时候需要的许多关于不同状态时,变量的定义。
- 尤其是在删除的操作上,递归可以将修改后的子树的值,通过返回值返回到母树上对应位置的地方,解决了链表结构不方便查找亲代的问题。
1.4 AVL树
- 从二插搜索树到AVL树:
- 在构造二叉搜索树的时候,我们发现,二叉树搜索树的构造过程严重依赖于起始序列的排序特性,也就是说,如果起始的数据直接是有序的话,那构造出来的二叉搜索树,树的高度就会非常地高,这显然不是我们想要的结果,于是AVL树就出现了,通过调整到平衡的过程,可以让二叉搜索树达到接近完全二叉树的程度,而这就是平衡二叉树的由来,其中最常见的是AVL树。他的特点是左右子树的高度差不超过1。
- 结合一组数组,介绍AVL树的4种调整做法。

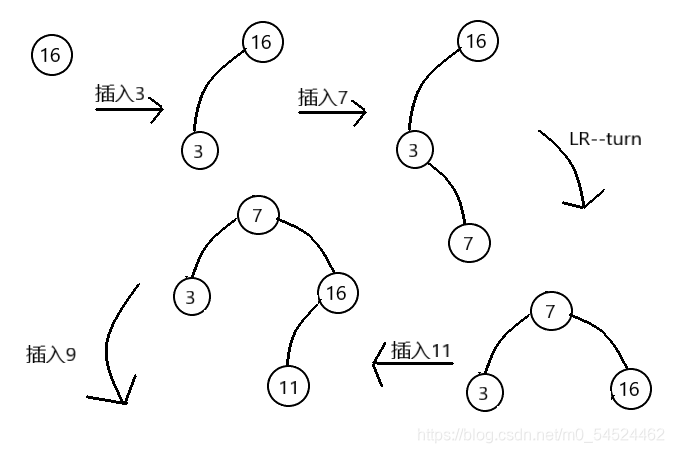
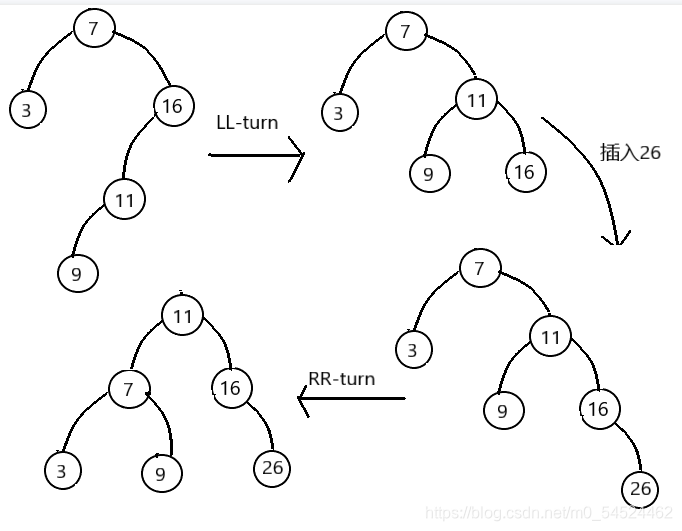
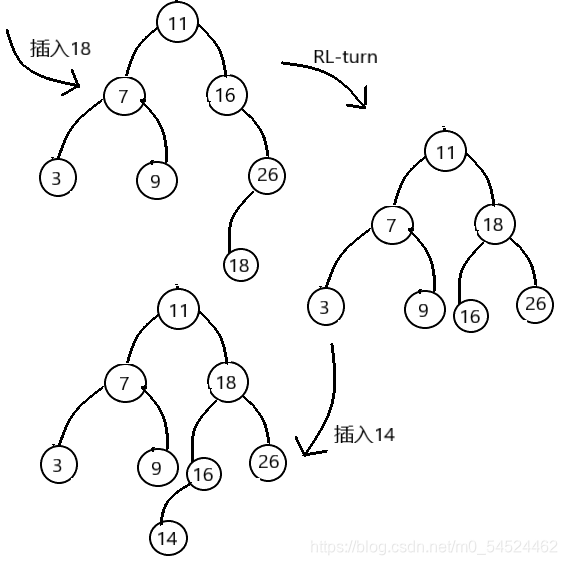
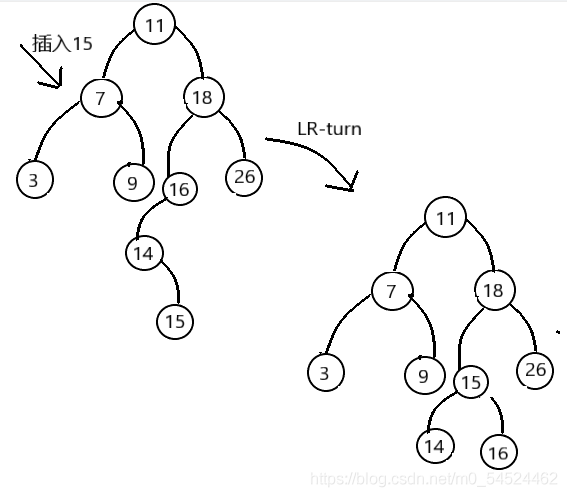
- 从例子我们可以了解到4种调整的特点:
- 对于LL型(RR型)的调整,我们是提拉最近的那个失衡结点的左(右)孩子,使其作为新的根节点,代替原来的失衡的结点的位置,如果这个被提拉的结点也有孩子的话,那它会顺着提拉的轨迹,成为与其碰撞的那个结点的孩子。
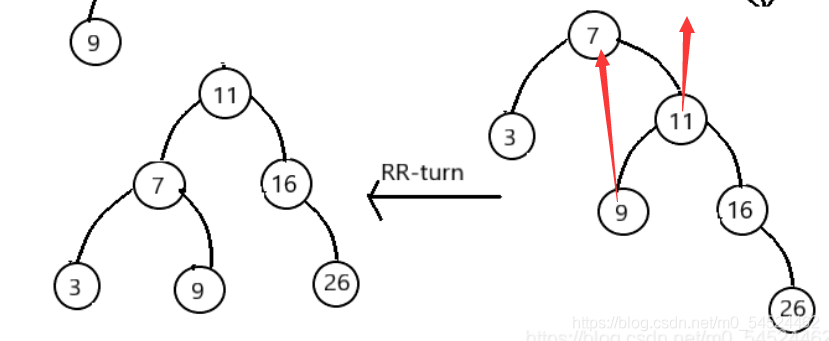
- 而对于RL(LR)型调整的话,我们是提拉最近的那个失衡结点的孙子,使其作为新的根节点,代替原来的失衡的结点的位置,然后切开了父亲和祖父间连接的那条联系,父亲自然落到下层成为孩子,祖父落到另一边成为另一个孩子。
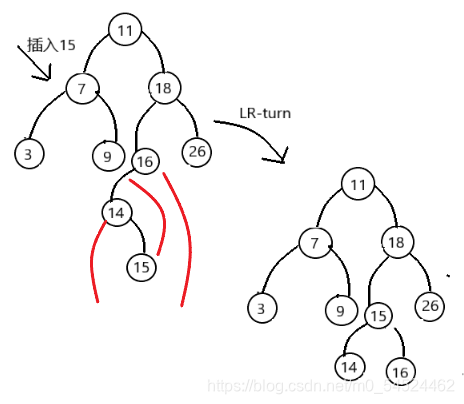
检验自己构造的树是否正确的一个利器是,利用二叉搜索树的一个特性,那就是中序遍历序列是一个递增的有序的序列。(左子树小,右子树大)
- 对于LL型(RR型)的调整,我们是提拉最近的那个失衡结点的左(右)孩子,使其作为新的根节点,代替原来的失衡的结点的位置,如果这个被提拉的结点也有孩子的话,那它会顺着提拉的轨迹,成为与其碰撞的那个结点的孩子。
- AVL树的高度和树的总节点数n的关系。
- 当高度大于1的时候,AVL树的高度和总结点数n的关系类似于菲波那契数列的关系。
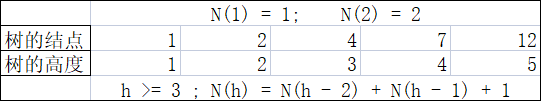
- 当高度大于1的时候,AVL树的高度和总结点数n的关系类似于菲波那契数列的关系。
- 介绍基于AVL树结构实现的STL容器map的特点、用法。
- 当下有用到的map容器的主要是两个主要的要点
- 第一,map容器可以用数组的方式来插入数据,而且它的地址可以是字符串!
- 第二,map容器可以调用count方法来查找是否存在某一个键值。
- 当下有用到的map容器的主要是两个主要的要点
更深入的map容器的学习,可以考虑研究一下这篇博客:
详细的map讲解
感谢作者codertcm
1.5 B-树和B+树
-
B-树和AVL树区别,其要解决什么问题?
- AVL树和二叉搜索树,都是用作内查找的数据结构,适用于数据量比较小的情况,即放在内存中的数据,而外存也需要数据存储结构,于是就有了B-树。B-树更倾向于是一种索引结构。
-
B-树定义。结合数据介绍B-树的插入、删除的操作,尤其是节点的合并、分裂的情况。
- B树的一些特性:
- 树中每个结点最多有m个子树(相对应的也就最多只能有m-1个关键字)
- 如果根结点不是叶子结点,则根节点最少有两棵子树。
- 对于所有的分支结点,最少要有【m/2】(取大于m/2的最小整数)。
- 所有的外部节点都在同一层上,且不带信息。
- 只支持随机查找。
- 在删除操作中,B-树可能合并,并让树的高度减少一层;在插入操作中,B-树可能分裂,并让树的高度增加一层。
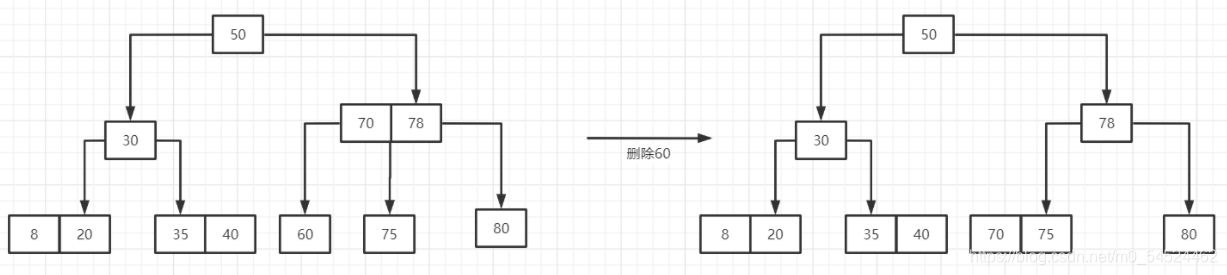
还是以PTA的题目为例:
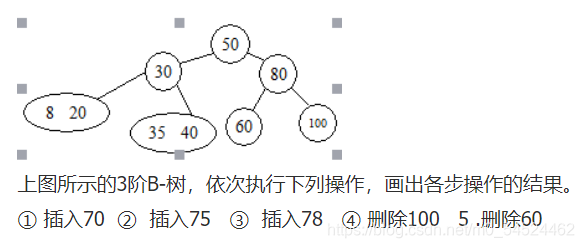
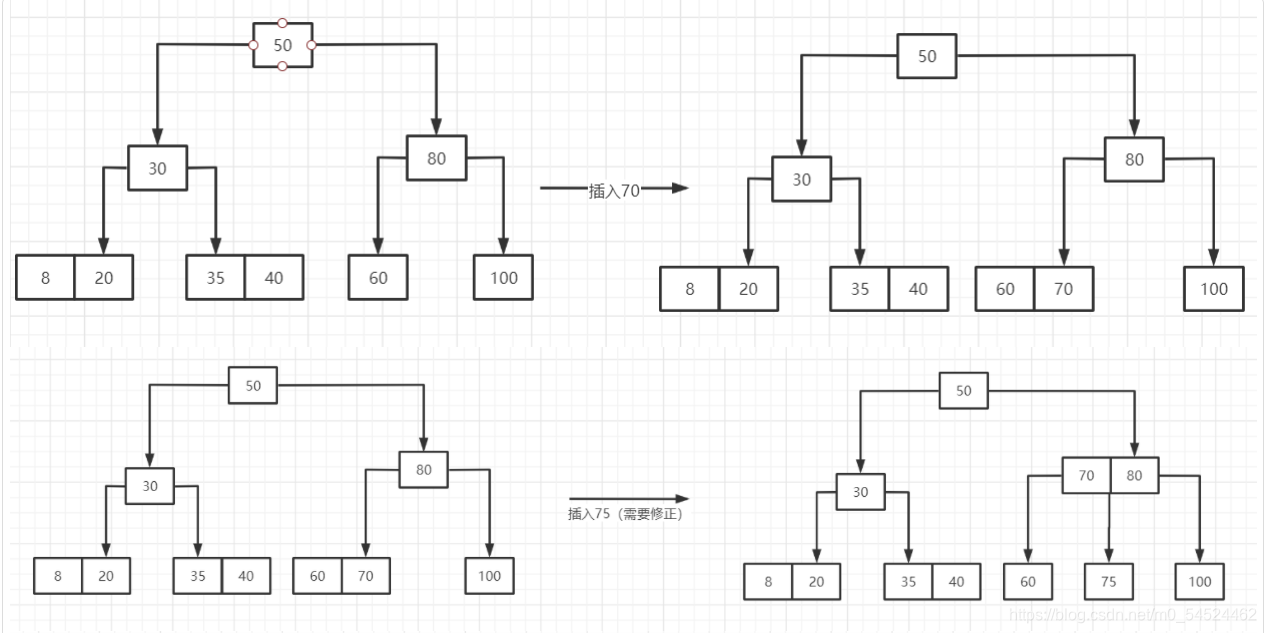
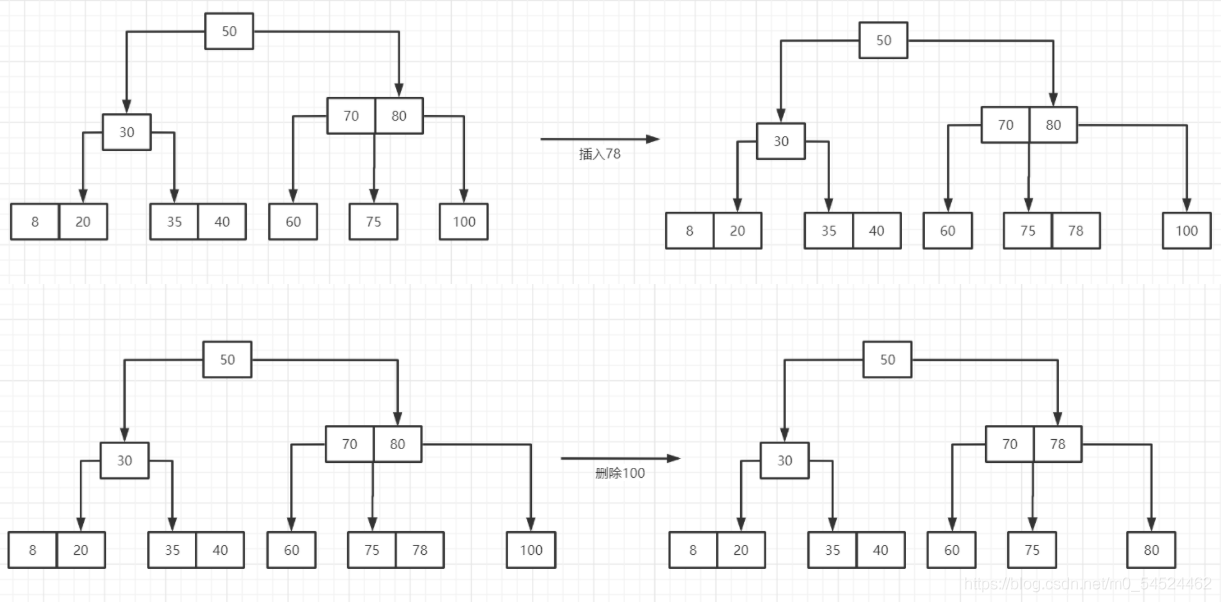
- 在插入的过程中,当插入使得结点包含的关键字的个数比它可以接纳的数量更多的时候,就会从中间取一个关键字,提拉到父亲结点上去,而原来的结点的关键字序列从中间一分为二作为被提拉的结点的子树。
- 在删除的过程中,如果删除的是两边的值,删完后两边的子树空了,这时候就要从父亲结点借,而父亲结点也要从另一边的子树借结点,直到使父亲节点和它的孩子结点的子树数和关键字数是符合规则的情况,而如果当子树的结点也不够借的时候,那父亲结点的关键字就会下沉于子树的关键字合并。
- 总结着来说,无论是插入还是删除, 他们最直接的影响都是影响某一个树结点的关键字的数目,而当关键字的数目增加到超过最大容量,或者减小到低于最小要求量,这种情况下,就会催生在子树层面的变化,从而再次让关键字的个数合理,变化的目的都是维持B-树保持原有的性质不受改变。
- B+树定义,其要解决问题
- B+树的性质:
- 每个分支结点最多有m棵子树。
- 根结点或者没有子树,或者最少有两棵子树。
- 除了根节点之外,其他分支结点最少有【m/2】(取大于m/2的最小整数)。
- 有n棵子树的结点有n个关键字
- 所有的叶子结点包含所有的关键字以及指向相应记录的指针,而且叶子结点按关键字大小顺序链接。
- 所有的分支结点仅包含它的各个子结点的最大值和指向它的子结点的指针。
- B+树支持顺序查找和随机查找。
- B+树用来解决文件的索引组织问题。另外B+树的插入、删除和查找在逻辑上和B-树类似。
- B+树的性质:
1.6 散列查找。
-
哈希表的设计
- 哈希表的结构体定义:
typedef int KeyType; //关键字类型 typedef char * InfoType; //其他数据类型 typedef struct node { KeyType key; //关键字域 InfoType data; //其他数据域 int count; //探查次数域 } HashTable[MaxSize]; //哈希表类型特点:1.存在关键字域,2.存在探查次数,3.需要预先确定哈希表的长度。- 哈希表的插入函数:
void InsertHT(HashTable ha, int& n,int m, KeyType k, int p) //哈希表插入数据,n表示哈希表数据个数,k为插入关键字,p为除数,m为哈希表长度 { int count; int adress; //求关键字对应的哈希地址; adress = k % p; //若对应位置已经被删除或者为空则直接插入即可 if (ha[adress].key == NULLKEY || ha[adress].key == DELKEY) { ha[adress].key = k; ha[adress].count = 1; } else //否则应查找直到找到可以插入的位置为止; { count = 1; //线性探测 do { adress = (adress + 1) % m; count++;//每探测一次的话,探测次数要增加; } while (ha[adress].key != NULLKEY && ha[adress].key != DELKEY); ha[adress].key = k; ha[adress].count = count; } //别忘了,新插入一个的话,列表的总数要加1 n++; }特点:1.先算哈希地址,这里采用除留余数法; 2.对于空结点或者被删结点可以直接插入; 3.遇到哈希冲突则使用线性探测法,并累计探测次数; 4.插入完后,对于表示哈希表长度的变量要加一- 哈希表的创建函数:
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p) //创建哈希表,x为输入数组,n输入数据个数,m为哈希表长度,这里假设m=p { int i; //初始化哈希表,赋空值 for (i = 0; i < m; i++) { ha[i].key = NULLKEY; ha[i].count = 0; } //初始化哈希表元素个数,得在插入建表之前。 int keepNum = n;//后面插入哈希表的时候要用到,所以要保存下来。 n = 0; //采用插入的方法一个一个把数据插入到哈希表中 for (i = 0; i < keepNum; i++) { InsertHT(ha, n, x[i], p); } }特点:1.需要初始化键值为NULLKEY和探测次数为0;2.建表前应归零表长;3.插入N个数据调用N次插入函数来建表。- 哈希表的查找
int SearchHT(HashTable ha, int p, KeyType k) //在哈希表中查找关键字k,找不到返回-1,找到返回查找地址。 { int count = 0; int m = p;//m为哈希表的长度 int adress = k % p; //查找的过程 while (ha[adress].key != NULLKEY && ha[adress].key != k && count <= m) { count++; adress = (adress + 1) % m; } if (ha[adress].key == k) { //找到了; return adress; } else { uns_count = count + 1;//这里要加1是因为最后查找不成功的那一次也要加上去! return -1; } }特点:1.当查找次数不超过表长,查找到的数据不为空,键值不等时,继续往下找;2.找到NULLKEY跳出。 -
结合数据介绍哈希表的构造及ASL成功、不成功的计算
以课堂派测试题目为例:

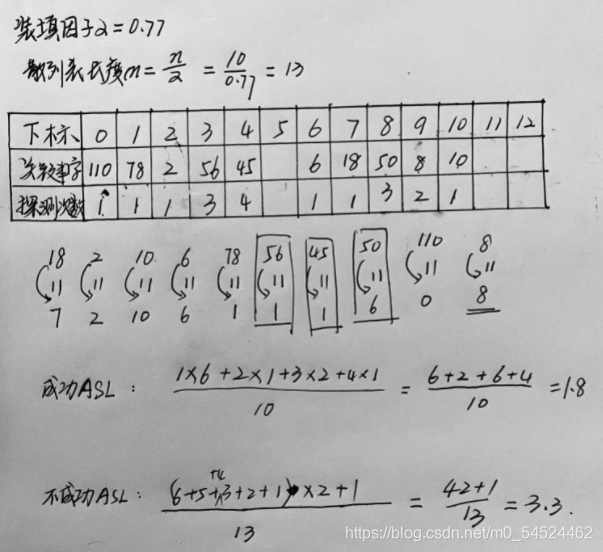
-
成功的ASL的分子来源于每个不同的数据的探测次数的累加,在代码上体现为count值的累加。分母来自于哈希表内载入的数据的个数。
-
不成功的ASL的分母来自于除留余数法当中p值的确定,而分子来源于,每一个可能的地址值探索到确认为查找不成功时的查找次数,要注意的是,对哈希表而言,查找不成功,这次也算有在查找的行列中,所以查找次数也要增加上去。
-
结合数据介绍哈希链的构造及ASL成功、不成功的计算
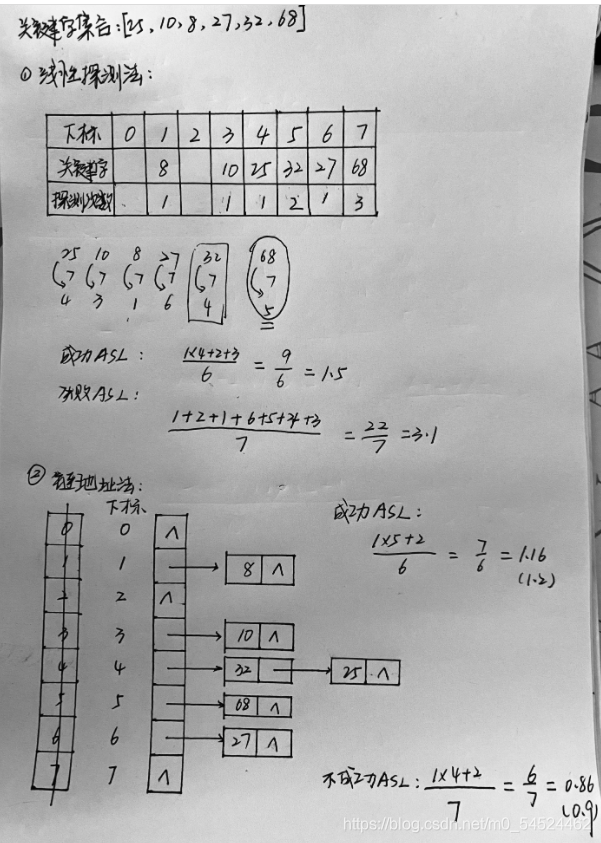
以课堂派测试题目为例:

-
首指针的地址是连续的,所以要相互连接起来。
-
每个结点结构体有两个区域,一个是指针域,一个是数字域这一点也要明确出来。
-
首指针的左侧要标清楚对应的地址的下标,且下标从0开始。
-
对于成功的ASL,分母依旧来自于存在的结点的个数,分子取决于,探测到对饮的数据的次数。
-
对于不成功的ASL,分母是除留余数法中p的值,分子取决于探测到空结点前,和存在的结点的比较的次数,且和空结点的比较,并不计入比较的次数当中。
2.PTA题目介绍(0--5分)
7-1 是否完全二叉搜索树
7-5(哈希链) 航空公司VIP客户查询
2.1 是否完全二叉搜索树(2分)
2.1.1 伪代码(贴代码,本题0分)
建二叉树
while(numb--)//numb为插入数据的个数
{
cin >> key;
调用Insert函数
}
Insert 函数
{
树空,T->data = key
树不空,
T->data > key ,递归插入左子树
T->data < key ,递归插入右子树
}
层次遍历
队列1,存key值。
队列2,存树结点。
按树的层次遍历来。
不同的是,
1. 子树无论空不空都入队。
2. 当结点为空结点时,入队的key值为#
当有#值入队时,标记get_block(遍历到了空结点)为真,如果后续再次出现数字,
则标记isCBBT(CBBT为完全平衡二叉树)为false。
3.输出队列1为层次遍历序列,其中#不输出。
4.依照isCBBT来判断是否为完全二叉树。
2.1.2 提交列表

本题的完成是在刚开始课程的时候,有一堂上机课,课上老师讲完具体的思路之后做的,当时一次性过了,背后是多次调试的结果。而出于各种原因,写博客时的时间离写这道题目的时间已经相距很远了,所以具体的内容其实已经记得不太清楚了。所以这里不作具体的阐述,把更多的内容放在第三部分去仔细分析。
2.1.3 本题知识点
- 二叉搜索树的递归建树
- 树的层次遍历的复习
- 完全二叉搜索树的层次遍历的序列,会保证当出现了第一个空结点之后,往后的结点,一定都是空结点,而不会再是非空结点。
- 本题最大的不同点在于,对于层次遍历中所遇到的空结点,此处采用的办法不再是忽略,而是也将其纳入树结点队列当中,并且定义它的key值为 '#',这样方便其在判定的时候可以方便使用性质来解决问题。
2.2 航空公司VIP客户查询(2分)
2.2.1 伪代码
建哈希表———>>纳入题目数据
初始化哈希链每个表头的next指针为NULL
for(执行N次)
{
输入id 和 mileage(里程数)
对里程数进行最小量修正
调用insert函数来建表
}
insert函数
{
计算哈希地址
查找是否已存在用户
if(exist)
{
里程直接累加
}
else
{
建立新结点
头插法,插入对应哈希链中
}
哈希函数的构造:
将身份证字符串转成具体数字,x当作10来处理
用除留余数法,p取100000 + 7(质数/奇数)
2.2.2 提交列表
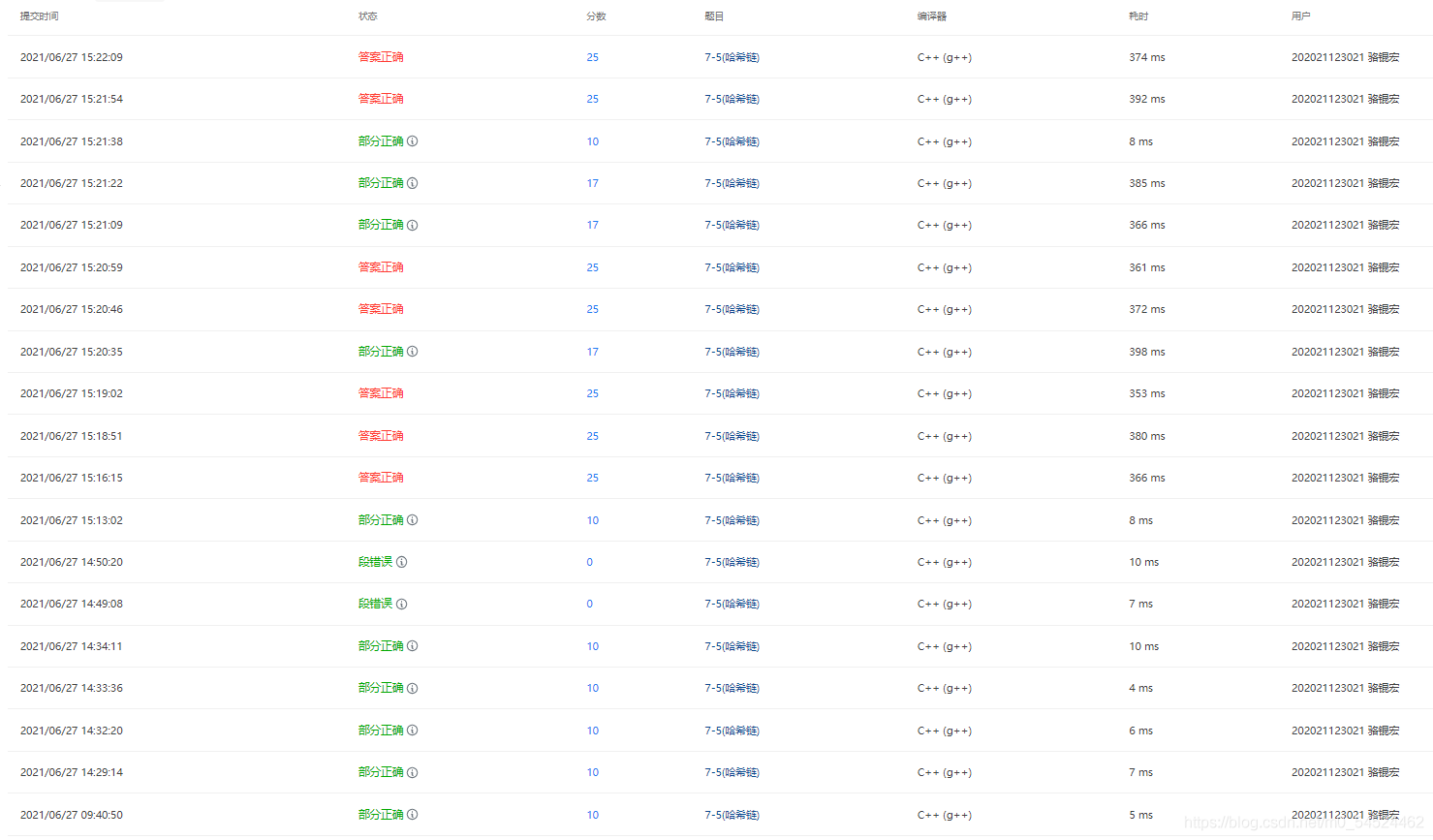
- 第一个时期:
- 用map容器来写这道题,结果被时间的测试点狠狠卡死在沙滩上,无奈绝望之际只好改过自新,老老实实用哈希链来写。map容器来构造的话其实是非常方便的,身份证可以用string来存,然后里程数用int来存,理清思路之后,用好map容器的 1.数组形式的插入法,2.count方法的查找法。那基本上这题的功能就可以实现了,但是问题是,时间开销不能满足该题的要求,会被狠狠卡死。
具体代码如下:
#include<iostream>
#include<string>
#include<map>
using namespace std;
map<string, int> VIPInfo;
int main()
{
int N;
int lowest_K;//最低的里程数
int i;
int M;
cin >> N >> lowest_K;
//收入数据
for (i = 0; i < N; i++)
{
string id;
int mileage;//里程数
cin >> id >> mileage;
//低于最低里程数的修正
if (mileage < lowest_K)
{
mileage = lowest_K;
}
if (VIPInfo[id] > 0)
{
VIPInfo[id] = VIPInfo[id] + mileage;
}
else//注意到没有被初始化的地址的值都是负值,所以可用0来判断行程累加的情况
{
VIPInfo[id] = mileage;
}
}
cin >> M;
//查找数据
for (i = 0; i < M; i++)
{
string search_id;
cin >> search_id;
if (VIPInfo.count(search_id))
{
cout << VIPInfo[search_id] << endl;
}
else
{
cout << "No Info" << endl;
}
}
return 0;
}
- 第二个时期:
2.2.3 本题知识点
- 第一次实验采用map容器再一次复习了map容器的插入方法,复习了map容器的count函数。
- 学会了hash链的结构体定义,插入数据,创建哈希表,查找数据的方法。
- 在调试的过程中,发现了对于身份证问题,如果要取所有的身份证号的数字来操作的话,需要的数据结构应该是使用long long才能够完全存储,如果使用int的话,会因为数据溢出而跳转到负值重新开始累加。(这个结论来自造cout输出和使用system("pause")函数来检验得到,本质上也复习了debug中常见的调试方法 )
- 哈希函数构造好了,对这题来说,依然不能解决最后的问题,还有一个很重要的知识点就是要控制好装填因子的问题。 哈希表开出来的长度必须要比可能的文件数1e5更大,这样子的话,算法执行的时间才能降下来。装填因子在0.6~0.9为最佳,但是有一个问题是,当你的哈希表的长度越大时,你初始化的时候,所需要的时间开销也会变得很大,这也是本题当中一个很致命的问题!
- 有多次修改哈希链的长度重复提交得到得一个惊人得结论就是,当哈希长度更大一些大到一定程度的时候,时间上的开销反而更小。
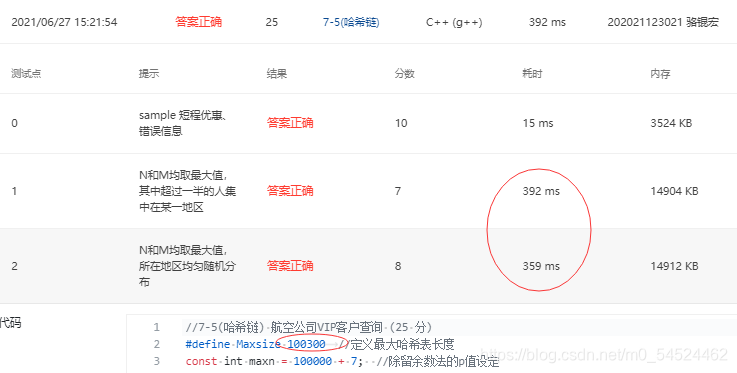
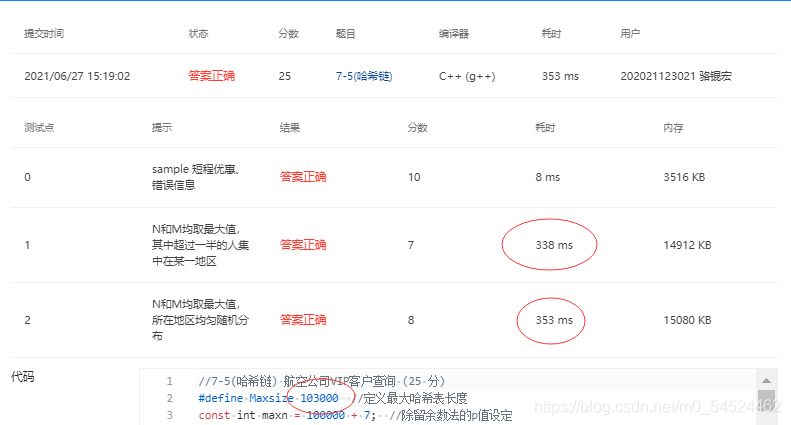
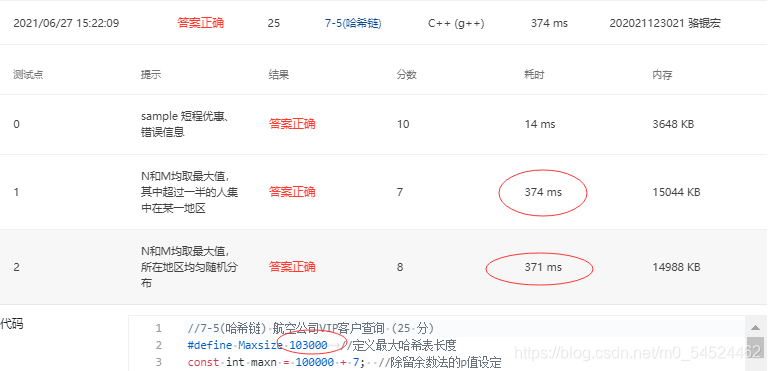
不过不排除存在测试数据的偶然性,只是看到这个现象,于是记录下来。
- 复习了字符数字转换为具体数字的操作 。
- 感悟:老实地说,关于哈希链的问题,这道题中可以讨论的内容还有很多,其中一个点就是我的哈希函数要如何去设置,会更好的地提高我算法的效率,这是是一个很需要时间去尝试的一个点,但是写这篇博客的时候。确确实实没有很多的时间了,所以这里只能大概留个具体的尾声等后期修改这篇博客的时候再来更新了。
2.3 基于词频的文件相似度(1分)
- 本题由于对倒排索引表的内容带有一定的疑惑和不彻底性,综合考虑到各项因素的前提下,决定参考网上的代码,并将该模块作为代码阅读题。暂时先保存对网上代码的思路上的思考,以及将补充网上的代码中需要学习的知识点的插叙。
2.3.1 伪代码
1.数据结构的选择。
* 用map<string,bool>的数组来存放文件,每一个数据代表一个文件,每个文件内可以存多个词组,
string用来存单词,bool用来标记存在一个单词,方便后续单词数量的统计。
* same[101][101] 二维数组是相似矩阵,两个下标是所对应的文件的编号,
存的值是两个文件共有的单词数量。
* num[101]用来存放对应下标的文件所含有的词组的个数。
2.数据的输入:
1.使用 cin.get()一个一个读取字符,直到遇到终止的字符'#'。
2.使用 toupper()函数将读入的小写字母转化为大写字母。
3.将输入的连续字母存入s_word数组(要求不超过10个)
4.中途遇到非字母字符或者超过10个的时候,都直接封尾,并存入map,
初始化s_word的下标继续读取数据。
3.数据的处理:
1.使用了C++中的迭代器,迭代统计每个map文件中的单词数量,并将每两个文件进行
一一的元素对比,如果数据相同的话,就在相似矩阵的对应位置的值加1.
2.对角线的元素本质上等于对应文件的单词数,可以对map求size()得到。
4.根据相似矩阵和长度表来计算相识度并输出。
用fixed函数和setprecision(1)来控制计算出来的数值的小数位数,并转化成文本形式。
2.3.2 具体代码分析
#include<iostream>
#include <map>
#include <iomanip>
#include <string>
#include <cstring>
using namespace std;
map<string, bool>m[101];//如果第i个文件存在单词word,则m[i][word] = true; bool 类型方便用来统计文件中究竟有多少个单词。
int same[101][101] = { 0 };//两两文件之间的相似矩阵;
int num[101] = { 0 };//用来存放对应文件编号所带有的文件个数;
int main()
{
//这一部分代码的功能是根据输入的文件及其信息,将单词数据进行格式处理。
int N;
cin >> N;
for (int i = 1; i <= N; i++)
{
char ch;
int cnt = 0;
char t_word[11];
while ((ch = toupper(cin.get())) != '#')//统一转换为大写字母
//cin.get()是获取一个字符的函数,类似于getchar()
//toupper()是将输入的小写字母转化为大写字母的函数
{
if (ch >= 'A' && ch <= 'Z')
{
if (cnt < 10) t_word[cnt++] = ch;/*如果cnt>=10,则cnt不会增加,停留在第10个字母后边,
直至遇到第一个非字母时将t_word[cnt]置为'\0'*/
}
else
{
t_word[cnt] = '\0';
if (cnt >= 3)
{
m[i][t_word] = true;
}
cnt = 0;
}
}
//统计每个文件所带有的单词个数存放在num表;
//计算两两文件之间对应的相似矩阵存放在same[][]中, same[i][j]表示 第i个文件和第j个文件所含有的相同的单词的个数。
map<string, bool>::iterator it;
//该语句定义了一个名为 it 的变量,变量的类型为 map<string,bool>
//iterator是C++中的迭代器,用于遍历容器中的每一个元素,因为对于容器我们不知道它的具体长度的话,
//就无法定量遍历,用迭代器的话,就能够很好地解决这个问题。
for (it = m[i].begin(); it != m[i].end(); it++)//代表从头到位遍历map,取遍map的每一个元素
{
for (int j = 0; j < i; j++)//判断是否有相同的单词,每有一个sam[i][j]就加一
//利用了矩阵的对称性来处理数据。
{
if (m[j][it->first] == true)
//it->first 指的是map定义中的第一个数据结构,此处指的是string类型。
same[i][j] = same[j][i] += 1;
else
same[i][j] = same[j][i] += 0;
}
}
//对角线的数据就是对应的文件编号的所存的词的个数。
same[i][i] = num[i] = m[i].size();
}
//输出相似度
int M;
cin >> M;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
cout << fixed << setprecision(1) << same[a][b] * 100.0 / (1.0 * (num[a] + num[b] - same[a][b])) << '%' << endl;
}
//fixed的用法:将数字按指定的小数位数进行取整,利用句号和逗号以十进制格式对该数进行格式设置,并以文本形式返回结果。
//setprecision的作用:用来控制显示浮点数值的有效数的数量,这里的1,表示保留1位小数。
return 0;
}
2.3.3 本题知识点
- 对头文件
iomainip的解释:这是c++中用来对所输入的内容进行格式上的处理的一个库,其中带有许多可用的方法。toupper函数可以将小写字母转化成大写字母。
详细可以参考该博客:iomainip
感谢作者
* 而本题中之所以会使用该库的原因在于,题中提到不对文件信息的大小写进行讨论,所以与其等接受具体的数据后再对数据进行各种条件判断的处理,不如直接在输入的时候就对格式进行统一的规划,这样在后续对数据进行比较的时候,会方便很多这也是本题使用该库的库文件的目的。
- 对于头文件
cstring的解释:其实cstring本质上就是C中的string.h只不过是过渡到C++中改了个名字而已。而本题之所以需要使用这个函数的原因在于,本题只讨论前10个字符,且需要对每个字符进行一一比对从而达到检查的目的,所以需要字符数组的很多操作函数的支持。cin.get()相当于getchar()
- 复习了
map容器的操作和使用。 map<string, bool>::iterator it定义了一个名称为it的迭代器,迭代器可以用于对容器内数据的遍历,通过begin()和end()来进行控制。因为对于容器我们不知道它的具体长度的话,就无法定量遍历,用迭代器的话,就能够很好地解决这个问题。fixed的用法:将数字按指定的小数位数进行取整,利用句号和逗号以十进制格式对该数进行格式设置,并以文本形式返回结果。setprecision的作用:用来控制显示浮点数值的有效数的数量,这里的1,表示保留1位小数。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号