2022_BUAA_OO 第一单元总结
2022_BUAA_OO 第一单元总结
OO第一单元的作业主题是表达式化简,主要的学习任务是熟悉Java语言基础操作,掌握面向对象的思想,学会并习惯用类来管理数据,实践分工协作的行为设计理念。以下便是我第一单元的学习心得与实践总结。
Homework1
代码结构分析
第一次作业涉及的表达式结构较为单一,实现的代码结构也相对简单。UML类图如下:
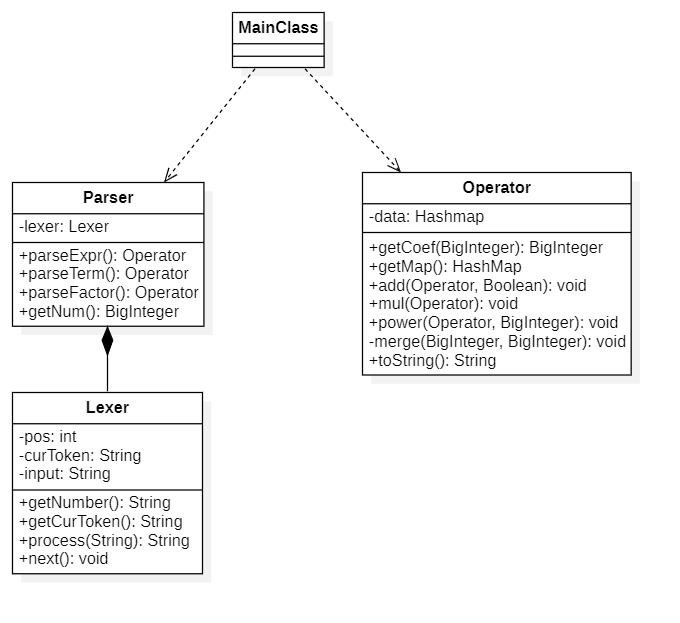
-
架构分析
这次作业中我使用了四个类,分为主函数类、Lexer类、Parser类以及存储单元算子类,主要借鉴了第一次单元训练中给出的递归下降的结构。利用Lexer、Parser类内部方法解析表达式,考虑到化简后表达式的基础项可以表示为
ax^b的形式,而具有相同指数的项之间又可以合并,故基础存储单元是利用指数检索系数的HashMap结构来存储所有基础的表达单元。 -
方法调用
在主类中利用输入的表达式字符串创建Lexer类对象,在Parser类对象中调用lexer方法来实现对表达式中的每个语义块进行提取,再用Parser中的方法递归下降,基础运算方法定义在了算子类中。
-
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getCurToken() | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.next() | 3 | 2 | 2 | 3 |
| Lexer.process(String) | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| Operator.Operator() | 0 | 1 | 1 | 1 |
| Operator.Operator(BigInteger, BigInteger) | 1 | 1 | 2 | 2 |
| Operator.add(Operator, Boolean) | 3 | 1 | 3 | 3 |
| Operator.getCoef(BigInteger) | 0 | 1 | 1 | 1 |
| Operator.getMap() | 0 | 1 | 1 | 1 |
| Operator.merge(BigInteger, BigInteger) | 5 | 1 | 3 | 3 |
| Operator.mul(Operator) | 8 | 1 | 7 | 7 |
| Operator.output(StringBuilder, BigInteger, String) | 4 | 1 | 2 | 4 |
| Operator.power(Operator, BigInteger) | 1 | 1 | 2 | 2 |
| Operator.toString() | 13 | 4 | 5 | 8 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.getNum() | 3 | 1 | 4 | 4 |
| Parser.parseExpr() | 6 | 1 | 5 | 6 |
| Parser.parseFactor() | 8 | 5 | 5 | 5 |
| Parser.parseTerm() | 1 | 1 | 2 | 2 |
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Lexer | 1.6 | 3 | 8 |
| MainClass | 2 | 2 | 2 |
| Operator | 3.6 | 13 | 36 |
| Parser | 3.2 | 5 | 16 |
从代码复杂度分析数据中可以看到,绝大多数方法的圈复杂度以及模块设计复杂度都相对合理,只有Operator类中的toString方法的基本复杂度较高,主要原因是该方法的实现较为随意,缺乏较好的设计,同时追求在该方法内完成表达式的全部化简工作,导致诸多选择结构、循环结构等不完整。整体上来看,各方法的iv(G)都较低,各类的OCavg也处于正常水平,说明整体设计的内聚度还是较高的。
评测方面
由于结构相对简单,本次作业在各次测试中均未出现bug,整个房间也没有出现成功hack的样例,几无收获。。。
Homework2
代码结构分析
本次作业加入了三角函数、求和函数以及自定义函数因子,表达式结构的复杂度骤然上升,我不得已选择了重构。UML类图如下:
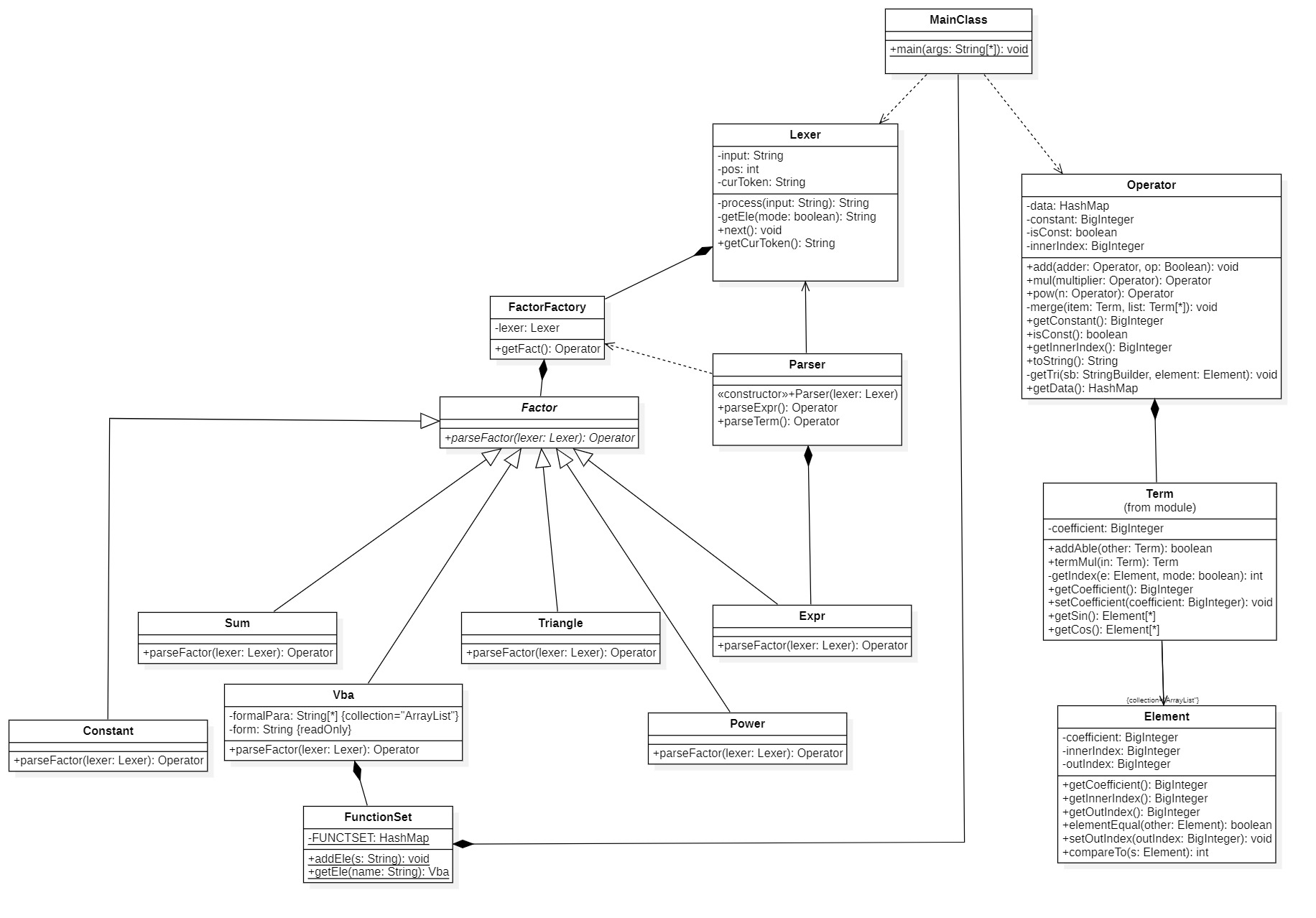
-
架构分析
在本次作业中,我新增抽象的因子类。常数因子、幂函数因子、三角函数因子等都继承于Factor类。
与第一次作业相比,主要区别在解析因子过程以及存储单元设计。
解析因子方面,由于因子的种类较多,所以我借鉴了工厂模式的设计思路,在对递归下降到对因子进行解析时,采用一个FactorFactory类来判别因子种类,继而返回不同因子的解析结果,对于表达式因子复用外层的Parser类中的parseExpr方法来提高代码的内聚度。
存储单元设计方面,本次作业将基本项取为
幂函数(三角函数项+...),底层Element用于存放单个三角函数内部指数(或常数)以及外部指数,Term类存放单个三角函数项的sin集,cos集以及其系数,Operator类则是利用外部指数索引三角表达式,三角表达式是三角项的ArrayList集。对于自定义函数,我定义了一个静态的FunctionSet类用来存放不同自定义函数的相关信息,在自定义函数因子中进行引用解析。
-
表达式解析
我采用的是边解析边下沉的方法。对表达式首先对其规范化(将**替换为^,去除空白字符等)。在parseExpr方法中解析出各个项,在parseFactor方法中,解析出各个因子,并将因子字符串传入FactorFactory中解析出对应的因子类型。
-
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| factor.Constant.parseFactor(Lexer) | 12 | 1 | 8 | 8 |
| factor.Expr.parseFactor(Lexer) | 1 | 2 | 2 | 2 |
| factor.FactorFactory.FactorFactory(Lexer) | 0 | 1 | 1 | 1 |
| factor.FactorFactory.getFact() | 6 | 6 | 6 | 6 |
| factor.Power.parseFactor(Lexer) | 2 | 2 | 2 | 2 |
| factor.Sum.parseFactor(Lexer) | 18 | 2 | 11 | 12 |
| factor.Triangle.parseFactor(Lexer) | 23 | 3 | 7 | 11 |
| factor.Vba.Vba(ArrayList |
0 | 1 | 1 | 1 |
| factor.Vba.parseFactor(Lexer) | 11 | 1 | 8 | 9 |
| module.Element.Element(BigInteger, BigInteger, BigInteger) | 0 | 1 | 1 | 1 |
| module.Element.Element(Element) | 0 | 1 | 1 | 1 |
| module.Element.compareTo(Element) | 4 | 5 | 4 | 5 |
| module.Element.elementEqual(Element) | 1 | 1 | 3 | 3 |
| module.Element.getCoefficient() | 0 | 1 | 1 | 1 |
| module.Element.getInnerIndex() | 0 | 1 | 1 | 1 |
| module.Element.getOutIndex() | 0 | 1 | 1 | 1 |
| module.Element.setOutIndex(BigInteger) | 0 | 1 | 1 | 1 |
| module.FunctionSet.addEle(String) | 3 | 1 | 3 | 3 |
| module.FunctionSet.getEle(String) | 0 | 1 | 1 | 1 |
| module.Operator.Operator() | 0 | 1 | 1 | 1 |
| module.Operator.Operator(BigInteger, ArrayList |
0 | 1 | 1 | 1 |
| module.Operator.Operator(BigInteger, BigInteger) | 2 | 1 | 1 | 2 |
| module.Operator.Operator(BigInteger, BigInteger, BigInteger, boolean, boolean, boolean) | 0 | 1 | 1 | 1 |
| module.Operator.add(Operator, Boolean) | 16 | 1 | 8 | 8 |
| module.Operator.getConstant() | 0 | 1 | 1 | 1 |
| module.Operator.getData() | 0 | 1 | 1 | 1 |
| module.Operator.getInnerIndex() | 0 | 1 | 1 | 1 |
| module.Operator.getTri(StringBuilder, Element) | 6 | 1 | 4 | 4 |
| module.Operator.isConst() | 0 | 1 | 1 | 1 |
| module.Operator.merge(Term, ArrayList |
9 | 4 | 5 | 5 |
| module.Operator.mul(Operator) | 10 | 1 | 5 | 5 |
| module.Operator.pow(Operator) | 1 | 1 | 2 | 2 |
| module.Operator.toString() | 42 | 3 | 12 | 14 |
| module.Term.Term(BigInteger) | 0 | 1 | 1 | 1 |
| module.Term.Term(BigInteger, BigInteger, BigInteger, boolean, boolean, boolean) | 8 | 1 | 3 | 5 |
| module.Term.Term(Term) | 2 | 1 | 3 | 3 |
| module.Term.addAble(Term) | 15 | 7 | 5 | 8 |
| module.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| module.Term.getCos() | 0 | 1 | 1 | 1 |
| module.Term.getIndex(Element, boolean) | 14 | 6 | 8 | 8 |
| module.Term.getSin() | 0 | 1 | 1 | 1 |
| module.Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| module.Term.termMul(Term) | 26 | 1 | 9 | 9 |
| proocess.Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| proocess.Lexer.getCurToken() | 0 | 1 | 1 | 1 |
| proocess.Lexer.getEle(boolean) | 8 | 1 | 6 | 6 |
| proocess.Lexer.next() | 4 | 2 | 3 | 4 |
| proocess.Lexer.process(String) | 0 | 1 | 1 | 1 |
| proocess.Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| proocess.Parser.parseExpr() | 6 | 1 | 5 | 6 |
| proocess.Parser.parseTerm() | 1 | 1 | 2 | 2 |
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| MainClass | 2 | 2 | 2 |
| factor.Constant | 8 | 8 | 8 |
| factor.Expr | 2 | 2 | 2 |
| factor.Factor | n/a | n/a | 0 |
| factor.FactorFactory | 3.5 | 6 | 7 |
| factor.Power | 2 | 2 | 2 |
| factor.Sum | 9 | 9 | 9 |
| factor.Triangle | 11 | 11 | 11 |
| factor.Vba | 4.5 | 8 | 9 |
| module.Element | 1.5 | 5 | 12 |
| module.FunctionSet | 2 | 3 | 4 |
| module.Operator | 3.79 | 16 | 43 |
| module.Term | 3.5 | 9 | 35 |
| proocess.Lexer | 2.2 | 4 | 11 |
| proocess.Parser | 2.33 | 4 | 7 |
从代码复杂度分析数据可以看出,Operator类的toString方法的基本复杂度和模块设计复杂度都严重超标,这是由于基本存储单元模块设计较为复杂,导致输出需要考虑的情况众多,同时反映出我没有使用工程化思想设计该方法,主要是针对测出的bug进行缝缝补补。Term类中的termMul方法的基本复杂度和模块设计复杂度都较高,究其原因是我没有对于sin和cos集提取方法来统一处理。而是利用较多重复代码来处理,同时由于管理sin,cos集的是ArrayList,我需要在该类中对这两类的顺序进行维护。
从类复杂度分析数据可以看出,由于存储单元的变化,基本计算方法的实现过程的判断条件众多,再加上toString的不良设计,导致其总圈复杂度超标。
测评方面
本次强测出现了一个bug,是由于我初定的三角函数内部只能是幂函数或常数类,而为了能够处理常数的常数次幂的形式,我在自定义函数内用实参替换形参时均添加了括号,而这导致了三角函数内部可能出现了表达式因子,无法进行解析。这是出现bug方法的基本情况:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| factor.Triangle.parseFactor(Lexer) | 23 | 3 | 7 | 11 |
可以看出其圈复杂度还是处于正常范围,但其代码行数较长,这也导致我不易发现该bug。
在互测环节,我被测出了一个bug,由于本次作业中我的优化做的相对草率,对于sin()0进行无脑替换,没有考虑指数可能带有前导0。同时我测出了其他同学没有正确处理类似于sin(-1)2的形式,由于优化考虑不到位而输出-sin(1)^2,还有同学没有考虑toString输出为空的情形而出错。
Homework3
代码结构分析
本次作业支持三角函数内部嵌套因子类型,以及自定义函数可以进行嵌套,我选择在第二次作业的基础上进行增量开发。UML类图如下:
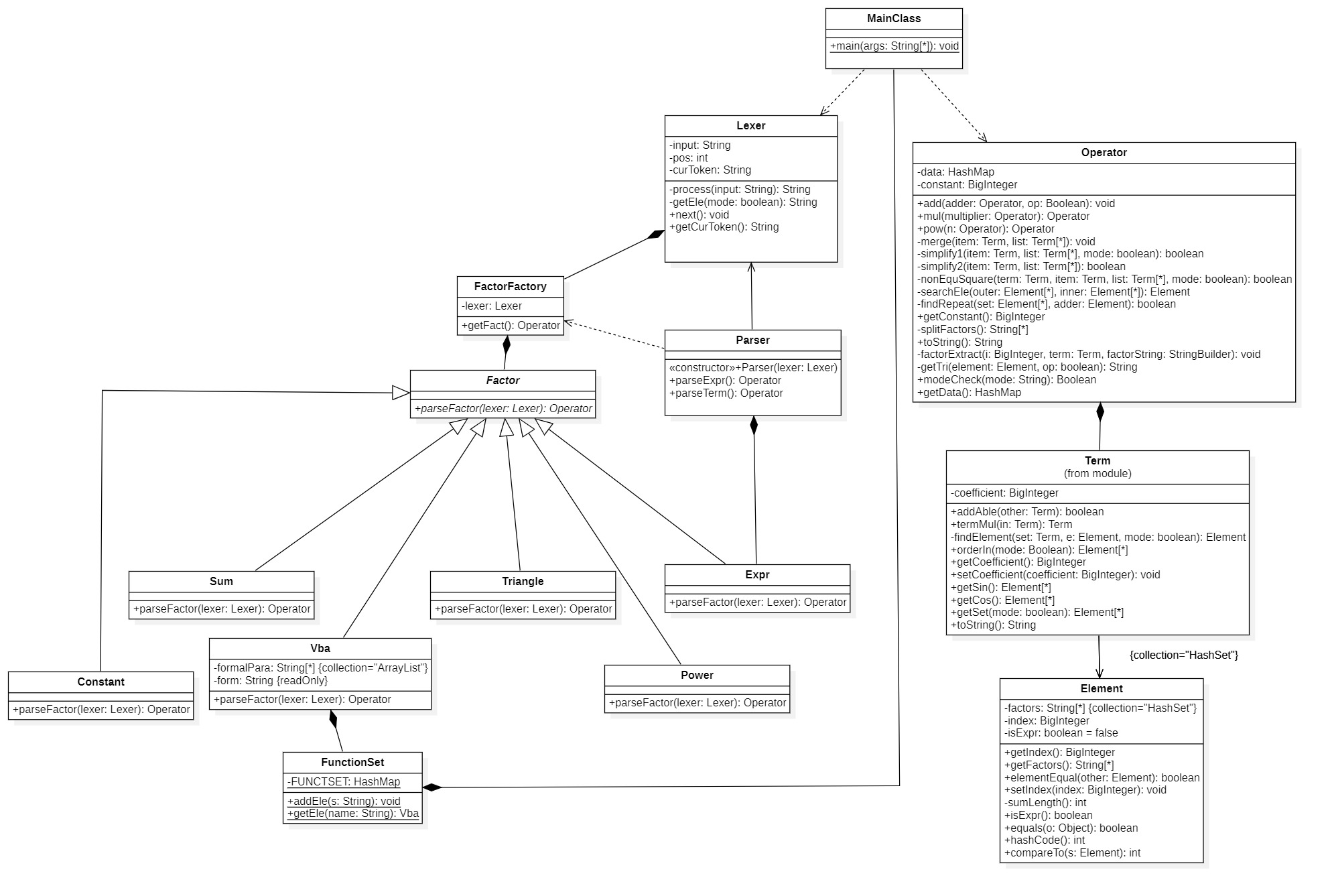
-
架构分析
由于第二次作业我已经对于嵌套的自定义函数进行了考虑,所以不需要修改太多。而为了能够存储嵌套的三角函数类型,基础存储单元的大体结构并没有改变,只是在最底层的Element类内部存放了三角函数内部存放的表达式的全部项,以HashSet
类型进行存储,这样就无需修改上层的计算方式。 而且体验过第二次作业中使用的ArrayList管理的诸多不便,我将其多修改为了HashSet,并且在Element类中对equals和hashcode方法进行了重写,这样大大简化了查找和比较过程,同时为了方便简化,我对于每个Element类中存储的项单元放入List中进行了排序,保证其具有一定的顺序,在进行嵌套时按照顺序连接各项以字符串形式与外层的项共同存储。
-
性能改善
除了基础的0次方、三角函数的简单优化外,我只对
asin^2+bcos^2、a-bsin^2、a-bcos^2等情况进行了优化,我采用的方式是在merge方法内,每有一项要合并入当前的主体表达式,若不能与某一项直接合并,就分别检测其是否满足上述三种形式若满足其中某种形式,与主体表达式的某一项合并后再将该项从主体表达式中取出,再递归调用merge函数以进行彻底的化简,每满足一项就不再进行其他形式的检测。若不满足则直接加入表达式内。这样做的代码量显著减少,同时简化效果较好,但由于没限制递归层数,极易出现TLE类型错误,或许应该增加测定函数执行时间的函数。 -
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| factor.Constant.getNum(Lexer) | 3 | 1 | 4 | 4 |
| factor.Constant.parseFactor(Lexer) | 2 | 1 | 2 | 2 |
| factor.Expr.parseFactor(Lexer) | 1 | 2 | 2 | 2 |
| factor.FactorFactory.FactorFactory(Lexer) | 0 | 1 | 1 | 1 |
| factor.FactorFactory.getFact() | 6 | 6 | 6 | 6 |
| factor.Power.parseFactor(Lexer) | 2 | 2 | 2 | 2 |
| factor.Sum.parseFactor(Lexer) | 18 | 2 | 11 | 12 |
| factor.Triangle.parseFactor(Lexer) | 21 | 3 | 6 | 11 |
| factor.Vba.Vba(ArrayList |
0 | 1 | 1 | 1 |
| factor.Vba.parseFactor(Lexer) | 5 | 1 | 5 | 5 |
| module.Element.Element() | 0 | 1 | 1 | 1 |
| module.Element.Element(BigInteger, HashSet |
0 | 1 | 1 | 1 |
| module.Element.Element(Element) | 0 | 1 | 1 | 1 |
| module.Element.compareTo(Element) | 4 | 5 | 4 | 5 |
| module.Element.elementEqual(Element) | 1 | 1 | 2 | 2 |
| module.Element.equals(Object) | 3 | 3 | 2 | 4 |
| module.Element.getFactors() | 0 | 1 | 1 | 1 |
| module.Element.getIndex() | 0 | 1 | 1 | 1 |
| module.Element.hashCode() | 0 | 1 | 1 | 1 |
| module.Element.isExpr() | 0 | 1 | 1 | 1 |
| module.Element.setIndex(BigInteger) | 0 | 1 | 1 | 1 |
| module.Element.sumLength() | 1 | 1 | 2 | 2 |
| module.FunctionSet.addEle(String) | 3 | 1 | 3 | 3 |
| module.FunctionSet.getEle(String) | 0 | 1 | 1 | 1 |
| module.Operator.Operator() | 0 | 1 | 1 | 1 |
| module.Operator.Operator(BigInteger, BigInteger) | 0 | 1 | 1 | 1 |
| module.Operator.Operator(BigInteger, HashSet |
0 | 1 | 1 | 1 |
| module.Operator.Operator(Operator, BigInteger, boolean, boolean, boolean, boolean) | 0 | 1 | 1 | 1 |
| module.Operator.add(Operator, Boolean) | 16 | 1 | 8 | 8 |
| module.Operator.factorExtract(BigInteger, Term, StringBuilder) | 34 | 1 | 11 | 11 |
| module.Operator.findRepeat(HashSet |
3 | 3 | 3 | 3 |
| module.Operator.getConstant() | 0 | 1 | 1 | 1 |
| module.Operator.getData() | 0 | 1 | 1 | 1 |
| module.Operator.getTri(Element, boolean) | 12 | 3 | 9 | 11 |
| module.Operator.merge(Term, HashSet |
12 | 4 | 6 | 6 |
| module.Operator.modeCheck(String) | 14 | 3 | 8 | 13 |
| module.Operator.mul(Operator) | 10 | 1 | 5 | 5 |
| module.Operator.nonEquSquare(Term, Term, HashSet |
9 | 1 | 11 | 12 |
| module.Operator.pow(Operator) | 1 | 1 | 2 | 2 |
| module.Operator.searchEle(HashSet |
5 | 3 | 2 | 4 |
| module.Operator.simplify1(Term, HashSet |
54 | 5 | 13 | 18 |
| module.Operator.simplify2(Term, HashSet |
35 | 11 | 14 | 17 |
| module.Operator.splitFactors() | 13 | 1 | 6 | 6 |
| module.Operator.toString() | 13 | 6 | 7 | 9 |
| module.Term.Term() | 0 | 1 | 1 | 1 |
| module.Term.Term(BigInteger) | 0 | 1 | 1 | 1 |
| module.Term.Term(BigInteger, HashSet |
8 | 1 | 3 | 5 |
| module.Term.Term(Term) | 2 | 1 | 3 | 3 |
| module.Term.addAble(Term) | 1 | 1 | 1 | 2 |
| module.Term.findElement(Term, Element, boolean) | 12 | 6 | 4 | 6 |
| module.Term.getCoefficient() | 0 | 1 | 1 | 1 |
| module.Term.getCos() | 0 | 1 | 1 | 1 |
| module.Term.getSet(boolean) | 2 | 2 | 1 | 2 |
| module.Term.getSin() | 0 | 1 | 1 | 1 |
| module.Term.orderIn(Boolean) | 2 | 1 | 2 | 2 |
| module.Term.setCoefficient(BigInteger) | 0 | 1 | 1 | 1 |
| module.Term.termMul(Term) | 8 | 1 | 5 | 5 |
| module.Term.toString() | 6 | 1 | 5 | 5 |
| proocess.Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| proocess.Lexer.getCurToken() | 0 | 1 | 1 | 1 |
| proocess.Lexer.getEle(boolean) | 8 | 1 | 6 | 6 |
| proocess.Lexer.next() | 4 | 2 | 3 | 4 |
| proocess.Lexer.process(String) | 0 | 1 | 1 | 1 |
| proocess.Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| proocess.Parser.parseExpr() | 6 | 1 | 5 | 6 |
| proocess.Parser.parseTerm() | 1 | 1 | 2 | 2 |
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| MainClass | 2 | 2 | 2 |
| factor.Constant | 3 | 4 | 6 |
| factor.Expr | 2 | 2 | 2 |
| factor.Factor | n/a | n/a | 0 |
| factor.FactorFactory | 3.5 | 6 | 7 |
| factor.Power | 2 | 2 | 2 |
| factor.Sum | 9 | 9 | 9 |
| factor.Triangle | 10 | 10 | 10 |
| factor.Vba | 3 | 5 | 6 |
| module.Element | 1.58 | 5 | 19 |
| module.FunctionSet | 2 | 3 | 4 |
| module.Operator | 3.65 | 14 | 43 |
| module.Term | 2.5 | 6 | 35 |
| proocess.Lexer | 2.2 | 4 | 11 |
| proocess.Parser | 2.33 | 4 | 7 |
从代码复杂度分析数据可以看出,由于本次对于toString方法内部提取了若干方法,同时进行了分层的封装处理,这个毒瘤终于被拿掉,但是简化相关的方法由于判断条件众多,简化形式众多而表现出较高的圈复杂度和模块设计复杂度、
从类复杂度分析来看,本次作业与上次情况大致相同,各类的内聚度依然较小。
评测方面
强测方面,由于忘记考虑三角函数内部嵌套的sum或自定义函数的解析结果可能是表达式,忘记添加括号,导致输出格式错误。这是出现bug方法的基本情况:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| factor.Triangle.parseFactor(Lexer) | 21 | 3 | 6 | 11 |
其圈复杂度和代码行数与其他方法相比并无异常,这主要是我考虑不周以及测试不到位引起的
互测方面,又由于sum内部循环变量的数据类型使用的是int类,而被房间的同学群起而攻。同时我发现有较多同学没有考虑常数的常数次幂的情况。
发现BUG策略
为实现覆盖性测试,我认为应当对知道数的形式化描述进行细致分析,然后从最底层的因子开始向上分析构建样例,尽量覆盖全部情况,同时注意指导书中给出的一些情况的特殊处理,如sum函数内的求和上限低于下限的情况。再次要在一些边缘数据上下功夫,如测试一些0特殊情况、因子单独出现、考虑选取的数据类型的范围。由于时间问题,我没有尝试构建自动化测试。
心得体会
-
提前做好寒假的Pre真的很重要(仍然记得第一周埋头苦学Java面向对象基础的狼狈样子),不过速成的效率还蛮高的,只不过对于一些语言特性还要做进一步地深入了解。
-
工厂模式具有很强的扩展性,它可以使创建过程对用户透明,在几次作业中对于单个因子的解析提供了很大的便利。
-
代码风格很重要,能够很大程度上提升代码的阅读效率。
-
讨论区真的有不少宝藏,从那里看到了不少神奇的化简方式,也在其引导下查阅资料学习了一些新知(深克隆、序列化、重写hash等等)。
-
要花足够的心思在测试环节,后两次作业出现的bug大多是我在做一些简单的优化是没有考虑周全导致的,优化无罪,不进行全面的测试才是原罪。
-
走一步想两步,要保证自己代码的可扩展性,毕竟重构多不是一件美事。



