算法第四章总结

 

贪心算法，指的是通过每一次得到的局部最优解从而得到全局的最优解。

贪心算法在很多问题下面是有用的，但是在另外一些问题（如：0-1背包问题）下就不能用贪心算法求解。此外，由于贪心算法经常涉及到最值操作，因此最值堆和sort函数【分别需要调用queue和algorithm头文件】就十分有用了。贪心算法题目可以大致分为以下几类。

1.直接贪心

顾明思义，就是直接把局部最优解拼出来，一般需要配合sort函数使用。

7-3 排队接水 (15 分)

有n个人在一个水龙头前排队接水，假如每个人接水的时间为Ti，请编程找出这n个人排队的一种顺序，使得n个人的平均等待时间最小。

输入格式:

共两行，第一行为n(1≤n≤1000)；第二行分别表示第1个人到第n个人每人的接水时间T1，T2，…，Tn，每个数据之间有1个空格。

输出格式:

输出为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。

输入样例:

10
56 12 1 99 1000 234 33 55 99 812

输出样例:

291.90

方法也很简单，直接通过计算得出要平均等待时间少，肯定要接水时间最少的人先接。

#include<iostream>
#include<algorithm>
#include<iomanip>
using namespace std;
int main()
{
     
    double a[1000];
    int i,n;
    cin>>n;
    for(i=0;i<n;i++)
    {
        cin>>a[i];
    }
    sort(a,a+n);
    double sum=0,suml=0;
    for(i=n;i>=0;i--)
    {
        sum+=a[i]*(n-i);
        suml+=a[i];
    }
    double sumall=sum-suml;
    sumall=sumall/n;
    cout<<setiosflags(ios::fixed)<<setprecision(2)<<sumall;
}

2.时间轴贪心

时间轴贪心最经典的问题就是单个会场效率最高问题了。一般题目都会让你定义一个线【或者可以用线表示的东西，如开始结束时间固定的活动】，然后你要做的就是通过一定顺序对这些线排序，最后得出结果。

1.按照结束时间排：单个效率最高，适用于容器（会场）固定的情况【或者能用单个线表示数据结构的题目】

2.按照开始时间排：总体效率最高，适用于容器（会场）无限的情况

【至于怎么排就不多说了吧...】

7-2 选点问题 (15 分)

数轴上有n个闭区间[ai, bi]。取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）。

输入格式:

第一行一个数字n，表示有n个闭区间。 下面n行，每行包含2个数字，表示闭区间[ai, bi]

输出格式:

一个整数，表示至少需要几个点

输入样例:

在这里给出一组输入。例如：

3
1 3
2 4
5 6

输出样例:

在这里给出相应的输出。例如：2

这是一道典型的结束时间排序问题，因为答案的结构其实是能用单线表示的。解决方法也很简单，直接用sum把一个圈子内的单个效率最高解求出，然后求这个解所包含的活动数量即可【因为其他活动已经被包含进去了】

#include<iostream>
#include<algorithm>
using namespace std;
struct huodong
{
    int start;
    int end;
};
bool cmp(huodong a,huodong b)
{
    return a.end < b.end;
}
int main()
{
    huodong a[500];
    int n,i;
    cin>>n;
    for(i=0;i<n;i++)
    {
        cin>>a[i].start;
        cin>>a[i].end;
    }
    sort(a,a+n,cmp);
    int flag=a[0].end;
    int sum=1;
    for(i=1;i<n;i++)
    {
        if(flag<a[i].start)
        {
            sum++;
            flag=a[i].end;
        }
    }
    cout<<sum;
}

7-5 会场安排问题 (15 分)

题目来源：王晓东《算法设计与分析》

假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。设计一个有效的 贪心算法进行安排。（这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个 顶点，不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数，相应于要找的最小 会场数。）

输入格式:

第一行有 1 个正整数k，表示有 k个待安排的活动。 接下来的 k行中，每行有 2个正整数，分别表示 k个待安排的活动开始时间和结束时间。时间 以 0 点开始的分钟计。

输出格式:

输出最少会场数。

输入样例:

5
1 23
12 28
25 35
27 80
36 50 

输出样例:

在这里给出相应的输出。例如：3

本题涉及到多个时间轴的分配，显然根据结论按照单会场结束时间的分法是肯定不行的，事实证明会出现以下情况

 

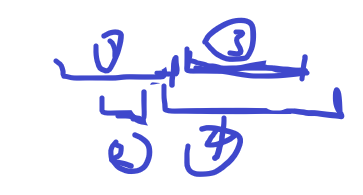
 如果按照结束时间分，需要3个会场，但是显然两个会场就可以搞定这些活动。

实际上按照开始时间分，也兼顾了总体的效率，防止出现按照结束时间分导致的总体效率过低的情况出现。

#include<iostream>
#include<algorithm>
using namespace std;
struct huodong
{
    int start;
    int end;
    bool have;
};
bool cmp(huodong a,huodong b)
{
    return a.start <= b.start;
}
/*bool okornot(huodong a[],int n)
{
    for(int i=0;i<n;i++)
    {
        if(a[i].have==false)
        {
            return false;
        }
    }
    return true;
}*/
int main()
{
    int i,sum=0,n;
    cin>>n;
    huodong a[500];
    for(i=0;i<n;i++)
    {
        cin>>a[i].start;
        cin>>a[i].end;
        a[i].have=false;
    }
    sort(a,a+n,cmp);
    int flag,count=n;
    while(/*!okornot(a,n)*/count>0)
    {
        flag=0;
        for(i=0;i<n;i++)
        {
            if(flag<=a[i].start && !a[i].have)
            {
                count--;
                a[i].have=true;
                flag=a[i].end;
            }
        }
        sum++;
    }
    
    cout<<sum;
    
} 

3.哈夫曼贪心

来源于哈夫曼树的组成【取两个小的，返回一个和】，适用于一些处理类问题【如：N合一，即处理后的材料会成为原材料】

为了方便计算一般都是使用priorty_queue这一数据结构，这个结构的特点是每次输出队列都会把最小的【当然你也可以自己定义比较函数】自动放到队列头

注意：这里判断“编码过程”是否结束的条件为队列长度>1因为每次结束都会把一个元素放入队列内

4-3 最优合并问题 (100 分)

题目来源：王晓东《算法设计与分析》

给定k 个排好序的序列, 用 2 路合并算法将这k 个序列合并成一个序列。 假设所采用的 2 路合并算法合并 2 个长度分别为m和n的序列需要m+n-1 次比较。试设 计一个算法确定合并这个序列的最优合并顺序，使所需的总比较次数最少。 为了进行比较，还需要确定合并这个序列的最差合并顺序，使所需的总比较次数最多。

输入格式:

第一行有 1 个正整数k，表示有 k个待合并序列。 第二行有 k个正整数，表示 k个待合并序列的长度。

输出格式:

输出最多比较次数和最少比较次数。

输入样例:

在这里给出一组输入。例如：

4
5 12 11 2 

输出样例:

在这里给出相应的输出。例如：

78 52

这道题的特点是你只要处理过两个序列后，会出现一个新的待合并序列，因此采用类似哈夫曼算法的贪心策略较为合适。

#include<iostream>
#include<queue>
using namespace std;

struct cmp{
    bool operator()(const int &s1,const int &s2)
    {
        return s1>s2;
    }
}; 

int main()
{
    priority_queue<int,vector<int>,cmp> q;
    priority_queue<int> qworst; 
    int n,a[1000],i,sum=0,sumworst=0;
    cin>>n;
    for(i=0;i<n;i++)
    {
        cin>>a[i];
        q.push(a[i]);
        qworst.push(a[i]);
    }
    while(q.size()>1)
    {
        int a=q.top();
        q.pop();
        int b=q.top();
        q.pop();
        sum=sum+(a+b-1);
        q.push(a+b);
    }
    while(qworst.size()>1)
    {
        int a=qworst.top();
        qworst.pop();
        int b=qworst.top();
        qworst.pop();
        sumworst=sumworst+(a+b-1);
        qworst.push(a+b);
    }
    cout<<sumworst<<" "<<sum;
} 

 

————————————————————————————————————————————————————————————————————————————————————————

4.满足问题，实质是看能不能满足眼前情况，如果不能满足就让它满足

用于一些值较为容易变化的贪心类问题。如，汽车加油【眼前情况：能不能撑到下一个加油站，如果不能就加油】

删除数字【删除这个数字，会不会使这个数字原位数的值变大，不会且有删数机会就删】

迪杰斯特拉也是满足问题的一种【先算离原点最短的】

7-1 汽车加油问题 (15 分)

 

题目来源：王晓东《算法设计与分析》

一辆汽车加满油后可行驶 n公里。旅途中有若干个加油站。设计一个有效算法，指出应 在哪些加油站停靠加油，使沿途加油次数最少。

输入格式:

第一行有 2 个正整数n和 k（k<=1000 )，表示汽车加满油后可行驶n公里，且旅途中有 k个加油站。 第二行有 k+1 个整数，表示第 k 个加油站与第k-1 个加油站之间的距离。 第 0 个加油站表示出发地，汽车已加满油。 第 k+1 个加油站表示目的地。

输出格式:

输出最少加油次数。如果无法到达目的地，则输出“No Solution!”。

输入样例:

7 7
1 2 3 4 5 1 6 6 

输出样例:

4

 

汽车加油问题的贪心选择性质：1。如果按照贪心算法得到的第一个加油的加油站为Ai，存在An加油【n<i】使得汽车加油次数更少，则把n加油替换成i加油所得汽车加油次数会<=原次数。

2.如果最优解A的加油油站存在Ai但是后续解B没有贪心得到，则B+1只会比原来的最优解A还要优【次数更少】，这和假设A是最优解矛盾。

因此，这道题符合贪心选择性质。

#include<iostream>
using namespace std;
int main()
{
    int canholdon,hold,sum=0;
    int n,i,j,gas[1003];
    
    cin>>hold>>n;
    for(i=0;i<=n;i++)
    {
        cin>>gas[i];
    }
    gas[n+1]=0;
    canholdon=hold;
    for(i=0;i<=n;i++)
    {
        if(gas[i]<=hold)
        {
            if(canholdon-gas[i]<0)
            {
                canholdon=hold;
                sum++;
                //continue;
            }
            /*else 
            {
                
            }*/
            canholdon-=gas[i];
        }
        else 
        {
            cout<<"No Solution!";
            return 0;
        }
    }
    cout<<sum;
}

 

5.本章学习遇到问题：这章相对来说没那么难，最有挑战性的可能就是证明了...

这次结对编程反而是最顺利的一次，我们依靠团队的力量在有限时间内把三道题全部解出，这让我非常有成就感~