Cholesky分解及一个例子

     定义： cholesky分解是一种将任意n阶对称正定矩阵A分解成下三角矩阵L的一种方法：

     

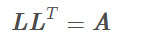
     其中，L称为Cholesky因子。如果L的对角元均为正数，则L是唯一确定的。

     Cholesky分解对于解决带有对称正定系数矩阵A的线性问题非常有效。在计算机中，直接求解Ax=b时间复杂度是很高的用cholesky法对A提前变换之后再计算会有效降低复杂度。计算方法如下：

     

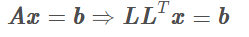
     其等价于

     

 

 

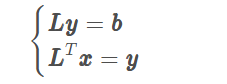
 令

      

 

 

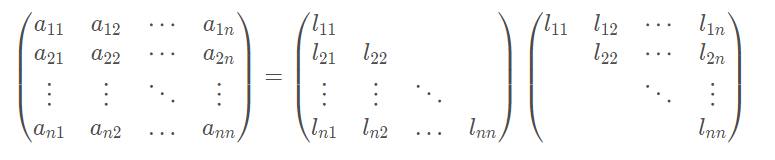
 则

       

 

 

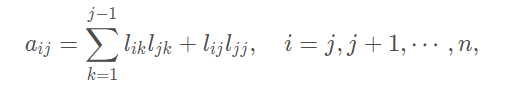
 则有

          

 

 

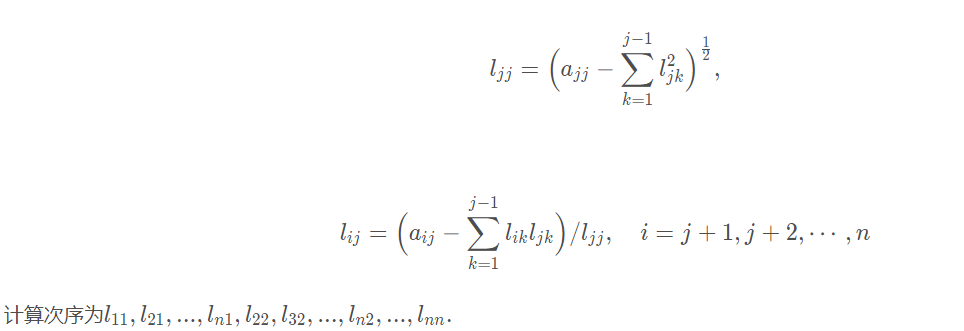
           注意，正定对称矩阵的行列式可以由下式得出：

           

 

 

          其中，L是由A得出的Cholesky因子。

例题
         用cholesky方法求解线性方程组A x = b 其中
                                                                        

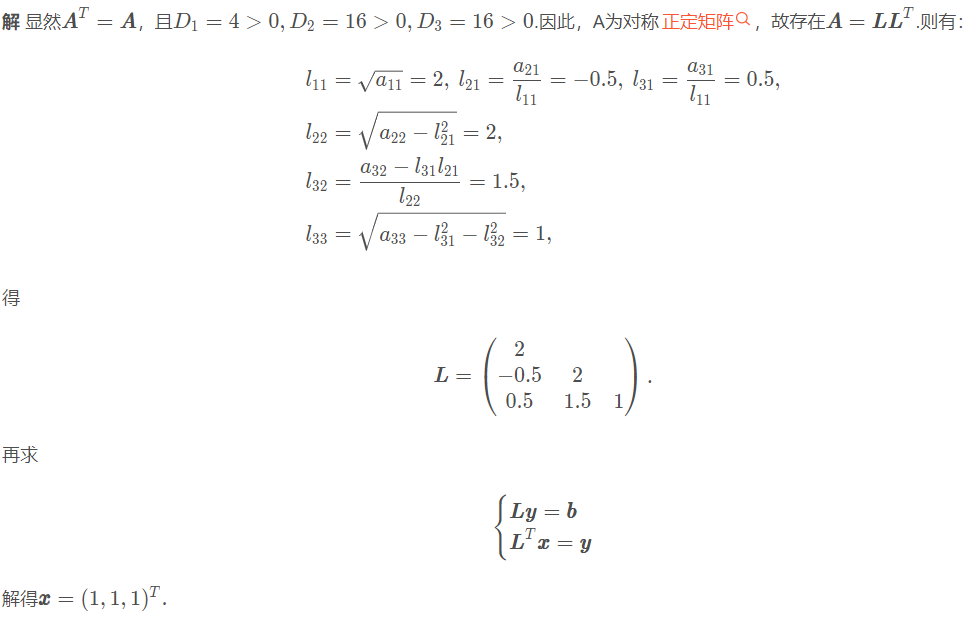
参考：

       https://blog.csdn.net/qq_41564404/article/details/88085073