香港中文大学(深圳) MAT1002 - Calculus II 笔记

PDF下载链接

笔记包括2025年春学期该课程的内容
所有知识点截图均来自王筱平教授的课件

更新：考前需要重点记忆的内容

  • 判断级数收敛的8种方法，括号里为使用前提

    1. N-th Term Test

    2. Integral Test (f：正、连续、不增)

    3. Direct Comparison Test (\(a_n\geq b_n\geq 0\))

    4. Limit Comparison Test (\(a_n,b_n>0\))

    5. Absolute Convergence Test

    6. Ratio Test

    7. Root Test

    8. Alternative Series Test

  • 常用麦克劳林级数

    \[\begin{align} \frac1{1-x}&=1+x+x^2+\cdots=\sum_{n=0}^{\infin}x^n,|x|<1\\ \frac1{1+x}&=1-x+x^2+\cdots=\sum_{n=0}^{\infin}(-1)^nx^n,|x|<1\\ e^x&=1+x+\frac{x^2}{2!}+\cdots=\sum_{n=0}^{\infin}\frac{x^n}{n!},x\in \mathbb R\\ sin\ x&=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots=\sum_{n=0}^{\infin}\frac{(-1)^nx^{2n+1}}{(2n+1)!},x\in \mathbb R\\ cos\ x&=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots=\sum_{n=0}^{\infin}\frac{(-1)^{n}x^{2n}}{(2n)!},x\in \mathbb R\\ ln(1+x)&=x-\frac{x^2}2+\frac{x^3}3-\cdots=\sum_{n=1}^{\infin}(-1)^{n-1}\frac{x^n}n,-1\leq x\leq 1\\ tan^{-1}x&=x-\frac{x^3}3+\frac{x^5}5-\cdots=\sum_{n=0}^{\infin}(-1)^n\frac{x^{2n+1}}{2n+1},|x|\leq 1 \end{align} \]

  • 极坐标曲线的弧长和面积公式

    • 弧长：\(L=\int_a^b\sqrt{(f(\theta))^2+(f'(\theta))^2}d\theta\)
    • 面积：\(A=\frac12\int_a^b(f(\theta))^2d\theta\)

  • \(\mathbb R^3\)中向量叉积公式：\(\overrightarrow w=<u_2v_3-u_3v_2,u_3v_1-u_1v_3,u_1v_2-u_2v_1>\)

  • 向量值函数相关

    • 单位切向量：\(\overrightarrow T=\frac{d\overrightarrow r}{ds}=\frac{{\overrightarrow r}'(t)}{||{\overrightarrow r}'(t)||}\)
    • 曲率：\(\kappa=||\frac{d\overrightarrow T}{ds}||=||\frac{d\overrightarrow T}{dt}||/||{\overrightarrow r}'(t)||\)
    • (主)单位法向量：\(\overrightarrow N=\frac 1{\kappa}\frac{d\overrightarrow T}{ds}=\frac{d\overrightarrow T/dt}{||d\overrightarrow T/dt||}\)

  • 用偏导数求平面曲线斜率：对于平面曲线\(F(x,y)=0\)，\(\frac{dy}{dx}=-\frac{F_x}{F_y}\)

    扩展到高维同理

  • 拉格朗日乘数法公式：\(\nabla f=\lambda\nabla g\)，更多限制情况下则为\(\nabla f=\sum \lambda_i\nabla g_i\)

  • 双变量函数的二次近似：用泰勒展开取一二次项

    \(f(x,y)\approx f(x_0,y_0)+(x-x_0)f_x(x_0,y_0)+(y-y_0)f_y(x_0,y_0)+\frac12 [(x-x_0)^2f_{xx}(x_0,y_0)+2(x-x_0)(y-y_0)f_{xy}(x_0,y_0)+(y-y_0)^2f_{yy}(x_0,y_0)]\)

  • 多重积分换元后需要额外乘上的系数：\(J(u,v)=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}\)

    普通坐标系转球坐标系，该系数为\(\rho^2sin\phi\)

  • 保守场的分量测试条件：\(\frac{\partial P}{\partial y}=\frac{\partial N}{\partial z},\frac{\partial M}{\partial z}=\frac{\partial P}{\partial x},\frac{\partial N}{\partial x}=\frac{\partial M}{\partial y}\)

  • 格林定理

    • \(\int_CF\cdot T\ ds=\int\int_R(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y})dA\)
    • \(\int_CF\cdot n\ ds=\int\int_R (\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y})dA\)

  • 参数曲面面积公式：\(S=\int\int_R |r_u\times r_v|du\ dv\)

  • 旋度公式：\(curl\ F=\nabla\times F\)，其中\(\nabla=<\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}>\)，计算结果为\(curl\ F=<\frac{\partial P}{\partial y}-\frac{\partial N}{\partial z},\frac{\partial M}{\partial z}-\frac{\partial P}{\partial x},\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}>\)

期中前

  • Infinite Sequences

    收敛性：\(\forall\epsilon>0,\exist N\ s.t.\ |a_n-L|<\epsilon(\forall n>N)\)

    有Diverge to \(\pm\infty\)的说法

    • Theorems & Properties

      • 函数极限的运算规则对数列极限同样适用(如\(lim_{n\to\infty}a_nb_n=L_a\cdot L_b\))
      • 若f在L处连续，且\(lim_{n\to\infty}a_n=L\)，则\(lim_{n\to\infty}f(a_n)=f(L)\)
      • Sandwich Theorem同样适用
      • 如果存在\(n_0\ s.t.\ a_n=f(n)\forall n\geq n_0\)，则\(\lim_{x\to\infty}f(x)=L\Rightarrow\lim_{n\to\infty}a_n=L\)

    • 常用序列极限(10.1中Theorem 5，要背)

      \[\begin{align} lim_{n\to\infin}\frac{ln\ n}{n}&=0\\ lim_{n\to\infin}\sqrt[n]n&=1\\ lim_{n\to\infin}x^{\frac 1n}&=1\ (x>0)\\ lim_{n\to\infin}x^n&=0\ (|x|<1)\\ lim_{n\to\infin}(1+\frac xn)^n&=e^x\ (x\in\mathbb R)\\ lim_{n\to\infin}\frac{x^n}{n!}&=0\ (x\in\mathbb R) \end{align} \]

    • Bounded Sequences 有界序列

      • \(\{a_n\}\) is bounded \(\Leftrightarrow\) it is bounded from both sides
      • \(\{a_n\}\) is convergent \(\Rightarrow\) is bounded
      • The Monotonic Sequence Theorem: 有界且单调的序列收敛

    • Applications & Tricks

      • 求序列的极限：直接当函数的极限求就行

        例：10.1.54

        image-20250228134701518

        例：10.1.74

        image-20250228135013648

      • 求Recursively Defined Seqences的极限

        例：10.1.98

        image-20250228135335334

  • Infinite Series: \(\sum_{n=1}^{\infty}a_n\)

    \(lim_{n\to\infty}S_n\) 存在 \(\Leftrightarrow\) 级数收敛

    • Geometric Series 几何级数：\(\sum_{n=0}^{\infty}ar^n\)

      收敛的充要条件：\(|r|<1\)

    • 判断级数收敛的方法

      1. N-th Term Test: \(lim_{n\to\infty}a_n=0\) (必要条件，不充分)

        例：10.2.64

        image-20250228140632044

      2. Integral Test: 若\(\exist N\ s.t.\ a_n=f(n)\geq 0\forall n\geq N\)，其中f是在\([N,\infty)\)上连续且不增的函数，则原级数收敛当且仅当\(\int_N^{\infty}f(x)dx\)收敛

        例：10.3.31

        image-20250228141344560

        例：10.3.37

        image-20250228141541027

      3. Direct Comparison Test: 若\(\exist N\ s.t.\ \forall n\geq N,a_n\geq b_n且a_n,b_n\geq 0\)，则a收敛\(\Rightarrow\)b收敛，b发散\(\Rightarrow\)a发散

        例：10.4.6

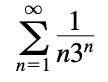
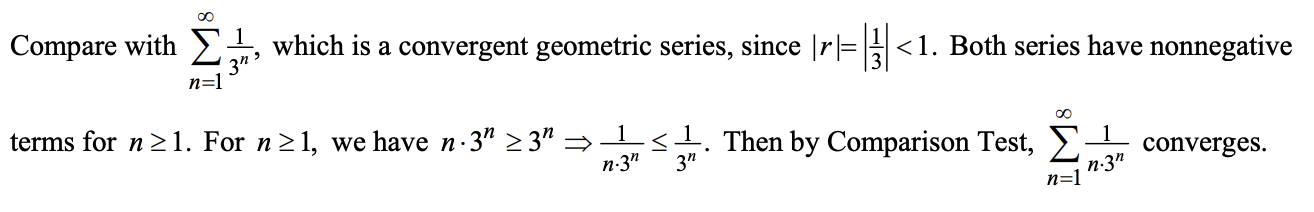
        image-20250228164637338 image-20250228164651057

      4. Limit Comparison Test: 若\(\exist N\ s.t.\ \forall n\geq N,a_n,b_n>0\)，令\(L=lim_{n\to\infty}\frac{a_n}{b_n}\)，则：

        • \(0<L<\infty\): a收敛\(\Leftrightarrow\)b收敛
        • \(L=0\): b收敛\(\Rightarrow\)a收敛
        • \(L=\infty\): b发散\(\Rightarrow\)a发散

        例：10.4.42

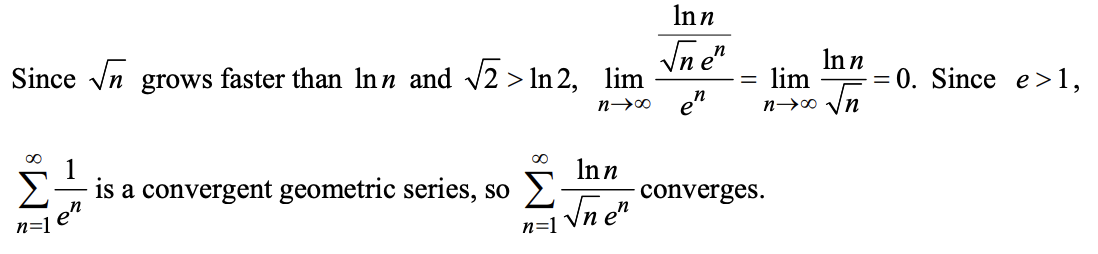
        image-20250228170743321

      5. Absolute Convergence Test: 若\(\sum|a_n|\)收敛，则\(\sum a_n\)收敛

        • Definition: 若\(\sum|a_n|\)收敛，则称\(\sum a_n\) converges absolutely
        • 若要求判断converges conditionally/absolutely还是发散，则对原级数和每项取绝对值后的级数分别判断(如果取完之后收敛，可以直接判为converges absolutely)

      6. Ratio Test: 令\(L=lim_{n\to\infty}|\frac{a_{n+1}}{a_n}|\)，则：

        • \(L<1\): Converges absolutely
        • \(L>1\): 发散
        • \(L=1\): 不好说

        例：10.5.35

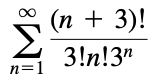
        image-20250228173059772 image-20250228173116546

      7. Root Test: 令\(L=\lim_{n\to\infty}\sqrt[n]{|a_n|}\)，则：

        • \(L<1\): Converges absolutely
        • \(L>1\): 发散
        • \(L=1\): 不好说

        例：10.5.40

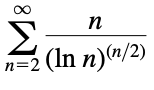
        image-20250228173234699 image-20250228173256563

      8. Alternative Series Test: 若为交错级数，且\(\exist N\ s.t.\ \forall n\geq N,u_n\geq u_{n+1};lim_{n\to\infty}u_n=0\)，则级数收敛

    • 对满足上面第8条中条件的Alternating Series值的估计

      \(L\)在\(S_k\)和\(S_{k+1}\)之间，\(|L-S_k|<u_{k+1}\)

    • 使用哪种Test(着重看4和5)：

      image-20250228154146143

  • Power Series 幂级数：\(\sum_{n=0}^{\infty}c_n(x-a)^n\)

    在幂级数中我们约定\(0^0=1\)

    • Radius of Convergence：以下三条中有一条成立

      1. 存在\(R\)满足\(\forall x\ s.t.\ |x-a|<R\)，级数收敛；\(\forall x\ s.t.\ |x-a|>R\)，级数发散；\(|x-a|=R\)，不一定

      2. 对任意\(R\)均收敛(\(R=\infty\))

      3. 在\(x=a\)收敛，其余均发散(\(R=0\))

      4. 求幂级数收敛范围：使用Ratio Test或Root Test，并对\(|x-a|=R\)单独检查

        例：10.7.22

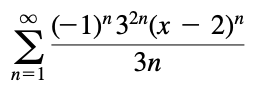
        image-20250301152821578 image-20250301152833404

    • 可以把幂级数一般形式和收敛形式中的x一起用一个代数式替换(Substitution)，但新未知数的收敛范围也要相应变化

    • 可以把两边同时积分或求导，但此时收敛范围边界处(\(|x-a|=R\))的收敛性可能会改变

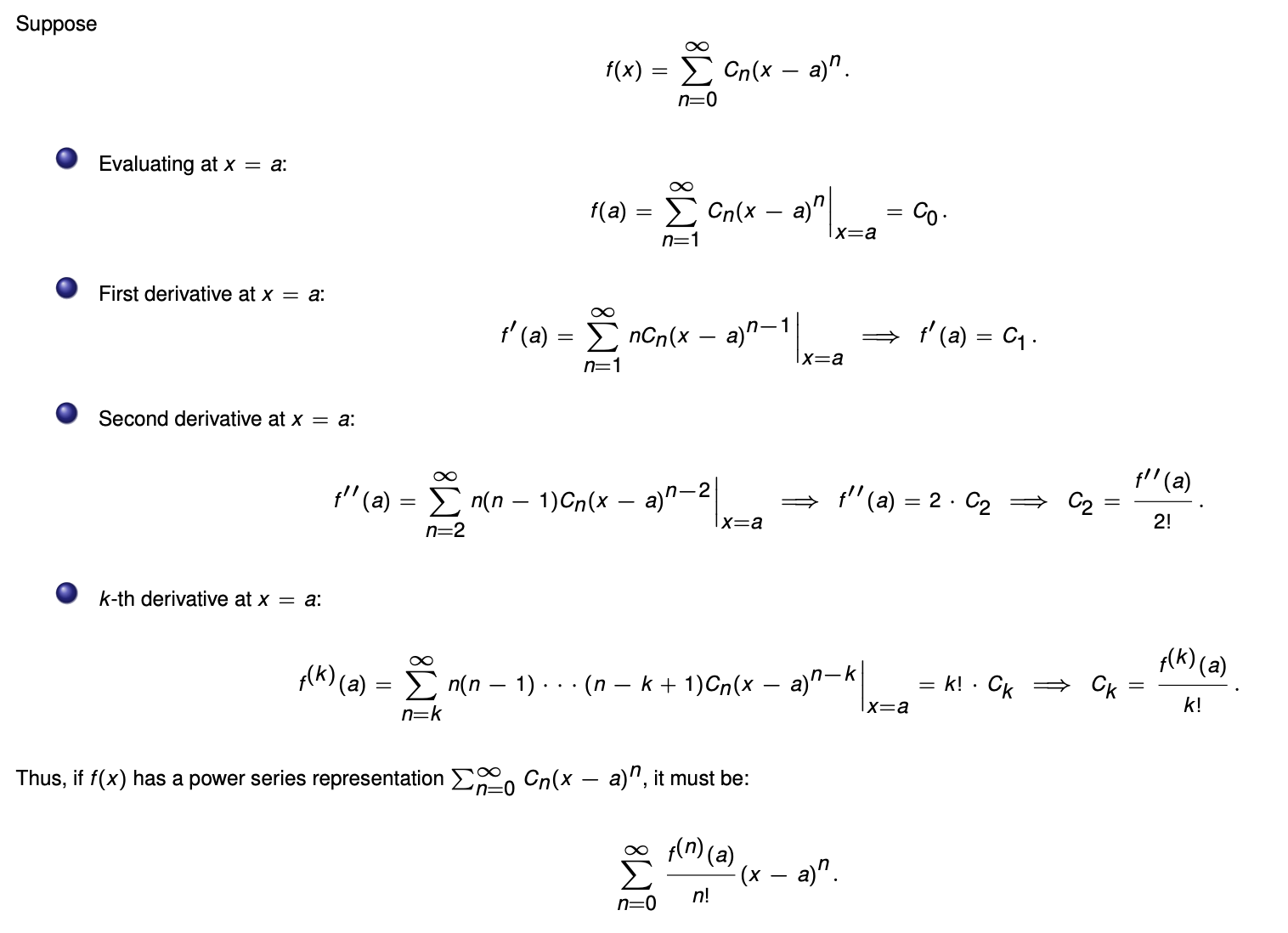
  • Taylor Series 泰勒级数：\(T(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n\)

    是一种用若干个多项式的和来拟合一个函数的方法

    推导过程：

    image-20250228200611149

    • Maclaurin Series 麦克劳林级数：\(a=0\)的情况

    • Taylor Polynomial 泰勒多项式：泰勒级数的一个前缀和

      \(f\)的以\(a\)为中心的\(n\)阶泰勒多项式：\(P_n(x)=\sum_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a)^k\)

    • 关于泰勒级数在收敛区间上是否收敛到原函数的问题

      • 不是解析函数，除了\(x=a\)处一定收敛，其他位置都不好说，例：\(f(x)=e^{-\frac1{x^2}(x\neq 0)},f(x)=0(x=0)\)，该函数的麦克劳林级数表现为一条直线\(y=0\)
      • 是解析函数，在收敛区间内部一定收敛到原函数，在\(|x-a|=R\)时可能收敛到原函数，可能收敛到其他值，可能发散

    • Taylor's Theorem 泰勒定理

      若\(f^{(n+1)}\)在\([a,x]\)上存在，则\(\exist c\in(a,x)\ s.t.\ f(x)=\sum_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a)^k+R_n(x)\)，其中余项\(R_n(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\)

      \(n=0\)的情况是Mean Value Theorem

      例：10.9.49

      image-20250301155105243 image-20250301155122735

    • Binomial Series 二项级数：\(\sum_{n=0}^{\infty}\binom{\alpha}nx^n\)

      当\(\alpha\)不为整数时，收敛半径\(R=1\)

      当\(x\to a\)时，\(R_n=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}=O((x-a)^{n+1})=o((x-a)^n)\)

    • 常用麦克劳林级数(要背)

      \[\begin{align} \frac1{1-x}&=1+x+x^2+\cdots=\sum_{n=0}^{\infin}x^n,|x|<1\\ \frac1{1+x}&=1-x+x^2+\cdots=\sum_{n=0}^{\infin}(-1)^nx^n,|x|<1\\ e^x&=1+x+\frac{x^2}{2!}+\cdots=\sum_{n=0}^{\infin}\frac{x^n}{n!},x\in \mathbb R\\ sin\ x&=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots=\sum_{n=0}^{\infin}\frac{(-1)^nx^{2n+1}}{(2n+1)!},x\in \mathbb R\\ cos\ x&=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots=\sum_{n=0}^{\infin}\frac{(-1)^{n}x^{2n}}{(2n)!},x\in \mathbb R\\ ln(1+x)&=x-\frac{x^2}2+\frac{x^3}3-\cdots=\sum_{n=1}^{\infin}(-1)^{n-1}\frac{x^n}n,-1\leq x\leq 1\\ tan^{-1}x&=x-\frac{x^3}3+\frac{x^5}5-\cdots=\sum_{n=0}^{\infin}(-1)^n\frac{x^{2n+1}}{2n+1},|x|\leq 1 \end{align} \]

    • Applications & Tricks

      • 用级数估计积分的值(精确到某个范围)：先展开再逐项积分，如果是交错级数，就取到第一个在给定区间内一定小于给定精度阈值的左边那一项

        例：10.10.28

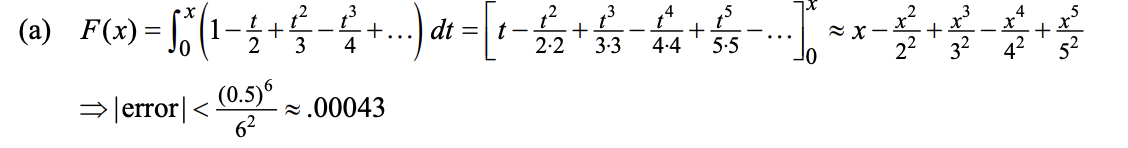
        image-20250226162540454

      • 用级数计算极限的值：将其中的一些项展开，极限会变得更好计算

        例：10.10.34

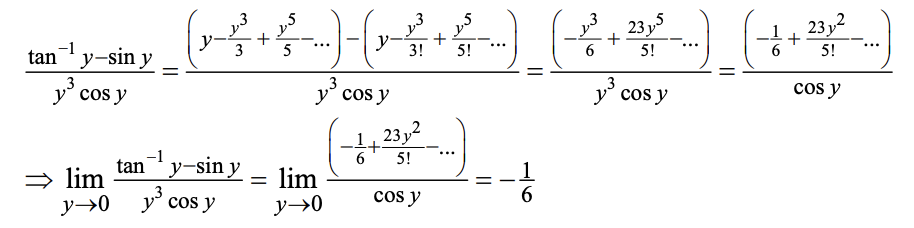
        image-20250226162944683

      • 已知展开式求原函数：需要把那几个常用麦克劳林级数背熟

  • Euler’s Identity 欧拉恒等式

    \(e^{i\theta}=cos\theta+i\ sin\theta\)或\(e^{i\pi}=-1\)

  • Parametric Curves 参数曲线

    \(\{(x,y):x=f(t),y=g(t),t\in I\}\)，其中\(I\)是一个区间，\(x=f(t),y=g(t)\)是Parametric Equations参数方程，\(t\)是参数

    • 弧长公式\(L=\int_a^b\sqrt{(f'(t))^2+(g'(t))^2}dt\)
    • 曲线下方面积公式\(A=\int_a^bg(t)f'(t)dt\)(假设\(f'(t)>0\))
    • Arc Length Differential\(dS=\sqrt{(f'(t))^2+(g'(t))^2}dt\)
    • 绕x轴旋转面积公式\(S=\int_a^b2\pi g(t)\sqrt{(f'(t))^2+(g'(t))^2}dt\)
    • 绕x轴旋转体积公式\(V=\int_a^b\pi(g(t))^2f'(t)dt\)

  • Polar Coordinates 极坐标：\((r,\theta)\)

    \((r,\theta)=(-r,\theta+\pi)\)

    极坐标转笛卡尔坐标：\(x=rcos\theta,y=rsin\theta\)

    笛卡尔坐标转极坐标：

    \(r^2=x^2+y^2,tan\theta=\frac yx(x\neq 0)\)

    \(\theta=\frac{\pi}2\ if\ y>0,\theta=\frac{3\pi}2\ if\ y<0(x=0)\)

    • Applications & Tricks

      • 转笛卡尔坐标方程：用\(r^2=x^2+y^2,x=rcos\theta,y=rsin\theta\)

        例：11.3.43

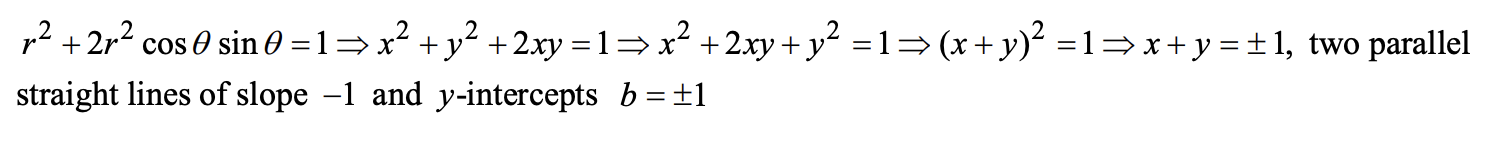
        image-20250227142343981

      • 转极坐标方程：同上

        例：11.3.65

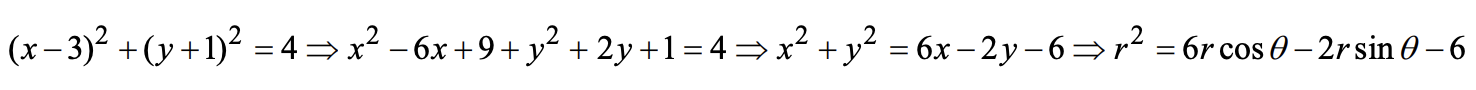
        image-20250227142834369

    Polar Curve 极坐标曲线：\(r=f(\theta)\)

    • 极坐标曲线某一处的斜率：\(x=f(\theta)cos\theta,y=f(\theta)sin\theta\)

      \(\frac{dy}{dx}=\frac{f(\theta)cos\theta+f'(\theta)sin\theta}{-f(\theta)sin\theta+f'(\theta)cos\theta}\)

    • 弧长公式\(L=\int_a^b\sqrt{(f(\theta))^2+(f'(\theta))^2}d\theta\)

    • 扇形面积公式\(A=\frac12\int_a^b(f(\theta))^2d\theta\)

      如果是两条曲线中间夹着的区域面积，就把f平方的差积分

    • 画图方法：先根据方程判断是否关于x/y/原点对称，然后取点用平滑曲线连接

    • 隐式定义的极坐标曲线可能不符合一般方程，一个\(\theta\)也可能对应多个\(r\)

      例：11.4.11

      image-20250227162935393

      后面画图还是得多看看

  • 3D Space

    三条轴的排列方式通常遵循右手法则

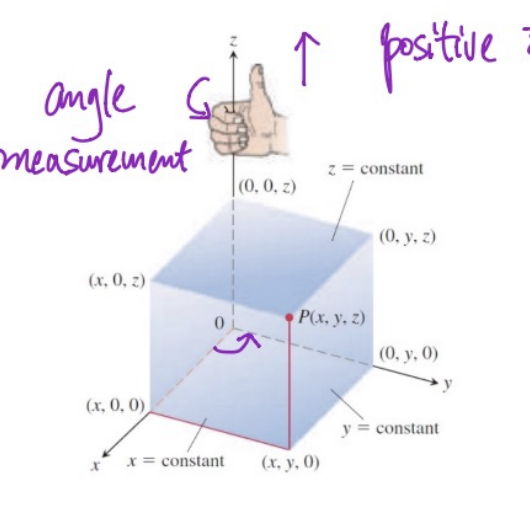
    image-20250227124733982

    \(\mathbb R^n\)中两点间距离为\((\sum_{i=1}^n(y_i-x_i)^2)^\frac12\)

    \(\mathbb R^3\)中向量的表示方法：\(\begin{pmatrix} a \\ b \\ c \end{pmatrix}\)或\(<a,b,c>\)

    Standard Unit Vectors 标准单位向量：\(<1,0,0>,<0,1,0>,<0,0,1>(i,j,k)\)

    求一个向量的方向(direction)时，应该用以\(i,j,k\)表示的一个长度为1的向量

  • Vectors in \(\mathbb R^3\)

    • 向量的投影：\(\overrightarrow u\)在\(\overrightarrow v\)上的投影\(proj_{\overrightarrow v}(\overrightarrow u)=||\overrightarrow u||\cdot(\frac{\overrightarrow u\cdot \overrightarrow v}{||\overrightarrow u||\cdot||\overrightarrow v||})\cdot \frac{\overrightarrow v}{||\overrightarrow v||}=\frac{\overrightarrow u\cdot\overrightarrow v}{||\overrightarrow v||^2}\overrightarrow v\)

      \(\frac{\overrightarrow u\cdot\overrightarrow v}{||\overrightarrow v||}\): scalar component of \(\overrightarrow u\) in the direction of \(\overrightarrow v\)

    • 向量的平行概念是针对非零向量而言的

    • \(\mathbb R^3\)中向量的叉积：令\(\overrightarrow w=\overrightarrow u \times \overrightarrow v\)

      • \(\overrightarrow w\)是\(\overrightarrow u,\overrightarrow v\)所确定平面的一个法向量

      • 右手法则：右手食指指向\(\overrightarrow u\)方向，中指指向\(\overrightarrow v\)方向，则拇指指向\(\overrightarrow w\)方向

      • \(\overrightarrow w=<u_2v_3-u_3v_2,u_3v_1-u_1v_3,u_1v_2-u_2v_1>\)

      • 叉积与行列式的关系

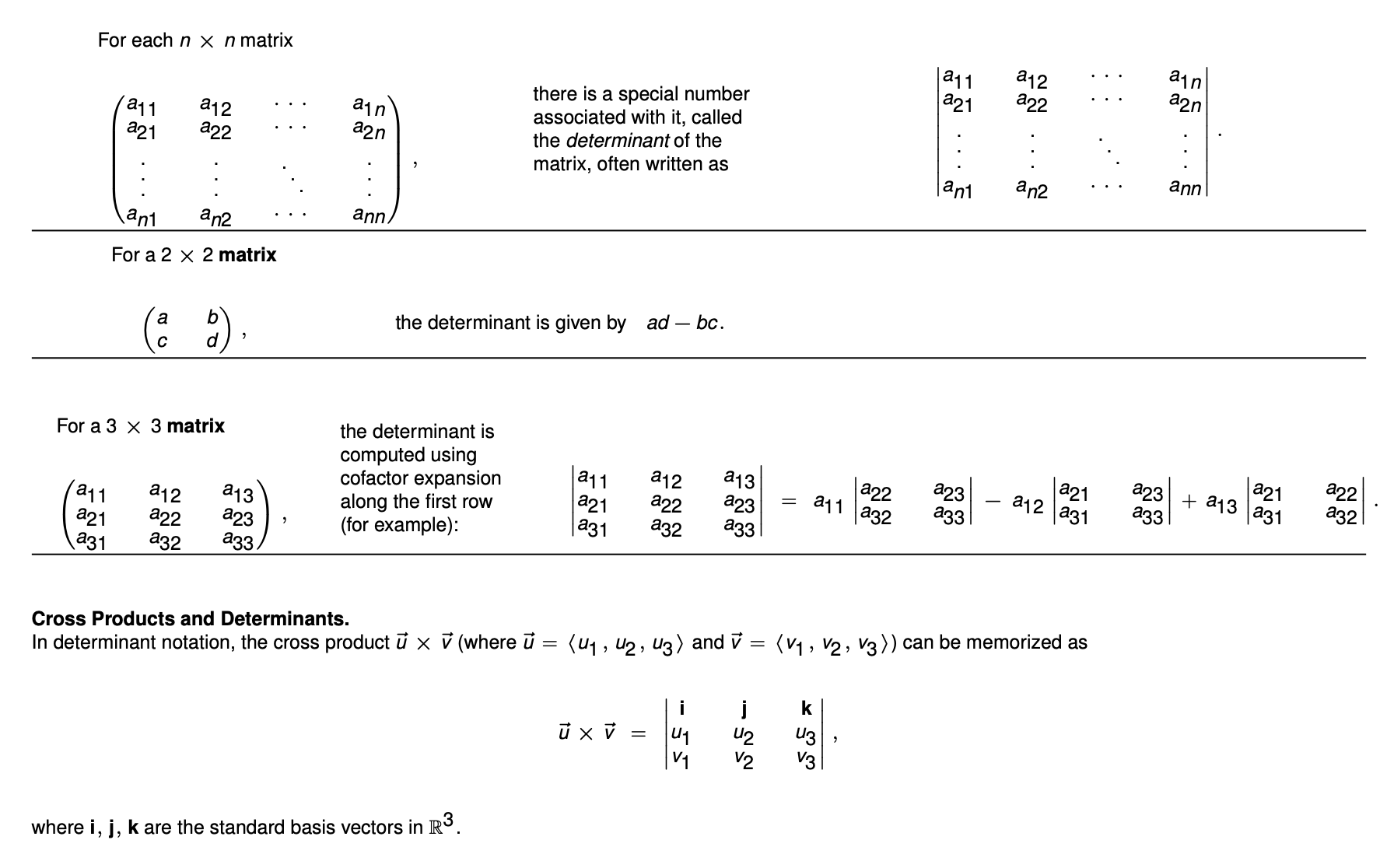
        image-20250302140711692

      • \(||\overrightarrow u\times \overrightarrow v||=||\overrightarrow u||\ \ ||\overrightarrow v||sin\theta\)

        image-20250302141613480

      • 叉积的长度是这两个向量围成的平行四边形的面积

      • 叉积的运算规则(交换律要取负，不遵循结合律，遵循分配律)

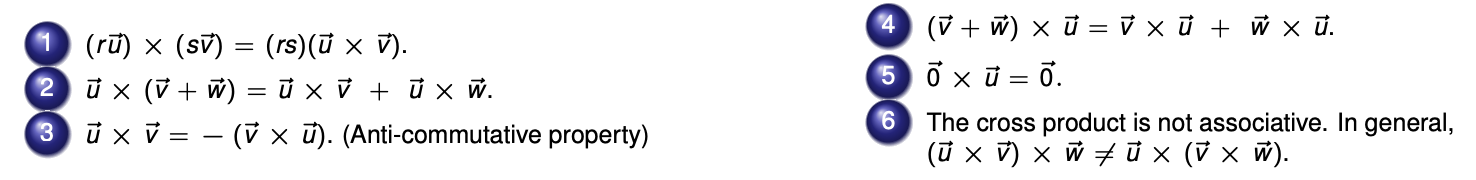
        image-20250302142159842

      • \((\overrightarrow u\times\overrightarrow v)\cdot \overrightarrow w\)的绝对值是这三个向量围成的平行六面体的体积

    • Torque 扭矩：衡量旋转趋势大小的矢量

      \(\overrightarrow\tau=\overrightarrow r\times\overrightarrow F\)

      右手定则：右手大拇指的方向是扭矩的方向，四指的方向是旋转的方向

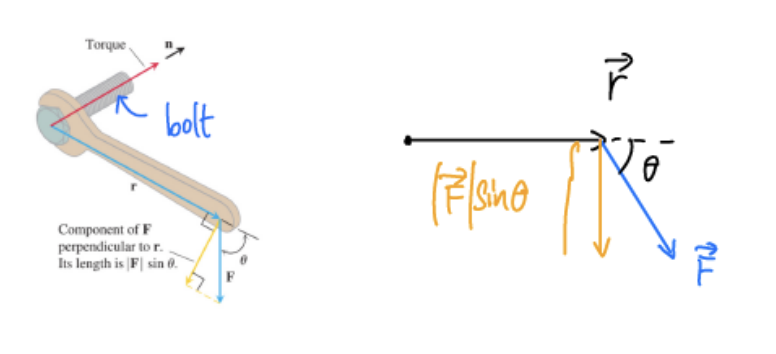
      image-20250302143824637

    • \(\mathbb R^3\)中的直线

      经过\(r_0(x_0,y_0,z_0)\)且与\(\overrightarrow v\)平行的一条直线可以表示为：\(\overrightarrow r(t)=\overrightarrow{r_0}+t\ \overrightarrow v\)

      \(\mathbb R^3\)中点到直线的距离：

      令P为直线上一点，S为直线外一点，\(d=\frac{||\overrightarrow{PS}\times \overrightarrow v||}{||\overrightarrow v||}\)

      例：12.5.38

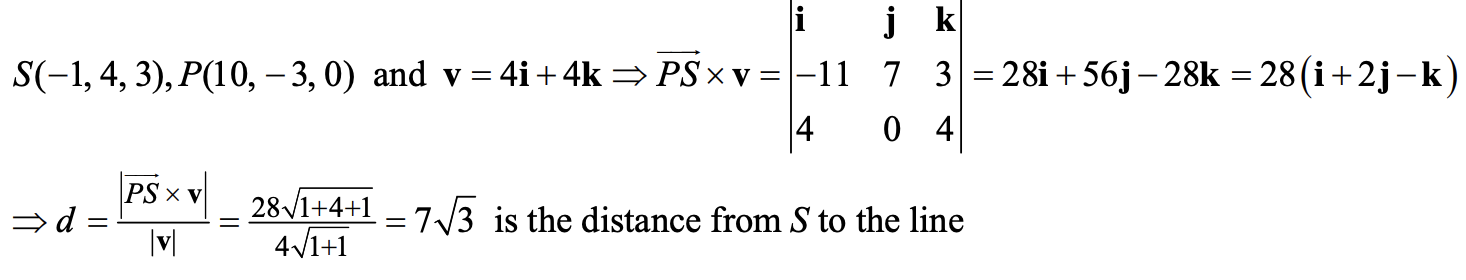
      image-20250302233206246 image-20250302233217800

    • \(\mathbb R^3\)中的平面

      令平面法向量为\(<A,B,C>\)，其与平面交点为\((x_0,y_0,z_0)\)，则\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)，\(Ax+By+Cz=D\)，其中\(D=Ax_0+By_0+Cz_0\)，\(<A,B,C>\)是这个平面的一个法向量

      \(\mathbb R^3\)中点到平面的距离：

      令P为平面上一点，S为平面外一点，\(d=\frac{|\overrightarrow{PS}\cdot \overrightarrow n|}{||\overrightarrow n||}\)

      例：12.5.45

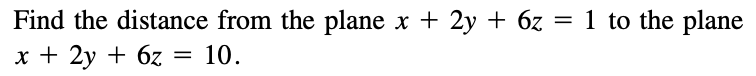
      image-20250302233438068 image-20250302233449778

      求两个平面交线的过程：求两平面法向量的叉积(也就是交线的方向向量)，然后解出交线上的一个点

      例：12.5.59

      image-20250302234218708 image-20250302234227962

      • Applications & Tricks

        根据交线求可能的平面方程

        例：12.5.69

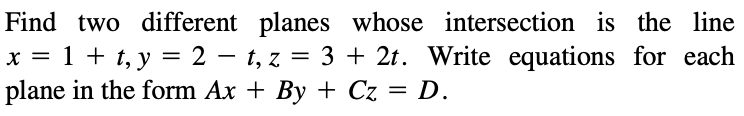
        image-20250302234831115 image-20250302234841834

    • 求两相离直线(Skew Lines)之间的距离：求出两方向向量的叉积，以其作为法向量构造两个包含这两条直线的平行平面，在两平面上分别取一个点用于计算两平面之间的距离

      image-20250302161154169

  • Cylinders and Quadric Surfaces 圆柱和二次曲面

    • Cylinder 圆柱：所有平行于给定直线且经过给定平面曲线的直线的集合(和以前说的那个圆柱不是一个东西)

    • Quadric Surfaces 二次曲面：所有满足一个二次等式的\((x,y,z)\)的集合

      • Hyperbolic Paraboloid 双曲抛物面：\(\frac{y^2}{b^2}-\frac{x^2}{a^2}=\frac zc\)

        image-20250302164639471

      • Elliptic Paraboloid 椭圆抛物面：\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac zc\)

        image-20250302164818547

      • Elliptic Cone 椭圆锥：\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z^2}{c^2}\)

        image-20250302165025314

  • Vector-Valued Functions 向量值函数

    \(\overrightarrow r(t)=<r_1(t)\cdots r_n(t)>\)，\(t\in I\)

    • 向量值函数的极限：\(lim_{t\to t_0}\overrightarrow r(t)=\overrightarrow L\Leftrightarrow \forall\epsilon>0,\exist c>0\ s.t.\ \forall|t-t_0|<c,||\overrightarrow r(t)-\overrightarrow L||<\epsilon\)

    • 性质： Component-Wise Limit 分量极限：\(lim_{t\to t_0}\overrightarrow r(t)=<L_1\cdots L_n>\Leftrightarrow \forall i,lim_{t\to t_0}{\overrightarrow r}_i(t)=L_i\)

    • Continuity 连续性：

      Continuous at \(t_0\Leftrightarrow lim_{t\to t_0}\overrightarrow r(t)=\overrightarrow r(t_0)\)

    • Differentiability 可微性：

      \({\overrightarrow r}'(t)=lim_{h\to 0}\frac{\overrightarrow r(t+h)-\overrightarrow r(t)}h\) exists

      若\({\overrightarrow r}'(t)\)连续且非零，则曲线的这个参数化光滑(Smooth)

      若\({\overrightarrow r}'(t)\)在仅定义域边界处为0，也不能算是光滑的(已向助教核实)；但一条曲线可以有多种参数化方式，只要有一种是光滑的，那这条曲线就是光滑的(见2025年期中考试判断题最后一题)，也就是说，"曲线光滑"和"参数化光滑"是两件事情

      求导运算规则：

      image-20250306154648787

    • Constant-Length Vector Functions:

      若\(\overrightarrow r(t)\)可微且长度恒定，则\(\forall t,\overrightarrow r(t)\cdot{\overrightarrow r}'(t)=0\)

    • Indefinite Integral 不定积分的定义：

      \(\int \overrightarrow r(t)dt=\overrightarrow R(t)+\overrightarrow C\)，其中\(\overrightarrow C\)是一个有定值的向量

    • Definite Integral 定积分的定义：

      \(\int_a^b\overrightarrow r(t)dt=<\int_a^br_1(t)dt\cdots\int_a^b r_n(t)dt>\)

      Fundamental Theorem of Calculus for Vector Functions: \(\int_a^b\overrightarrow r(t)dt=\overrightarrow R(b)-\overrightarrow R(a)\)

    • Applications & Tricks

      • 射弹的最大高度

        以与地面的角度\(\alpha\)和初速度\(v_0\)发射的射弹的最大高度为\(\frac{v_0^2sin^2(\alpha)}{2g}\)

    • 弧长公式：

      \(L=\int_a^b||{\overrightarrow r}'(t)||dt=\int_a^b\sqrt{(f'(t))^2+(g'(t))^2+(h'(t))^2}dt\ (n=3)\)

      跟参数曲线的弧长公式很像

      例：13.3.12

      image-20250307203249891 image-20250307203302450

      若弧长\(s\)一直变化，则可以用\(s\)表示\(t\)，写出一个新的轨迹公式(Re-parameterize the helix with respect to arc length measured from...)

      • \(\overrightarrow T=\frac{d\overrightarrow r}{ds}\) Unit Tangent Vector 单位切向量

      • Curvature 曲率：描述曲线在一点弯曲程度的量

        \(\kappa=||\frac{d\overrightarrow T}{ds}||=||\frac{d\overrightarrow T}{dt}||/||{\overrightarrow r}'(t)||\)

      • \(\overrightarrow N=\frac 1{\kappa}\frac{d\overrightarrow T}{ds}=\frac{d\overrightarrow T/dt}{||d\overrightarrow T/dt||}\) Principal Unit Normal Vector 主单位法向量，表示着单位切向量变化的方向，永远和单位切向量垂直(计算的时候一般用等式最右边那个)

        例：13.4.12

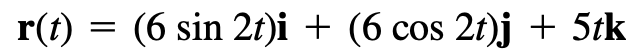
        image-20250307220124532 image-20250307220133757

      • Osculating Circle 密切圆：对于一条平面曲线，点\(P\)处的密切圆是与这条曲线有相同切线和曲率、圆心在主单位法向量方向的圆，半径为\(\frac1{\kappa}\)(这个按照曲率定义硬算能算出来)

考前默写：8种判断级数收敛性方法，7个常用麦克劳林级数，3个极坐标换算常用公式，极坐标曲线弧长、面积公式，\(\mathbb R^3\)中的叉积公式，向量值函数的单位切向量、单位法向量、曲率公式

期中后

  • Functions of Several Variables 多变量函数 基础部分

    • 双变量函数的极限：若\(\forall \epsilon>0,\exist c>0\ s.t.\ \forall(x,y)\in D,0<\sqrt{(x-x_0)^2+(y-y_0)^2}<c\Rightarrow |f(x,y)-L|<\epsilon\)，则\(lim_{(x,y)\to(x_0,y_0)}f(x,y)=L\)

      更多变量的函数类似

      极限的各种运算规则和Sandwich Theorem仍然适用

      例：14.2.17

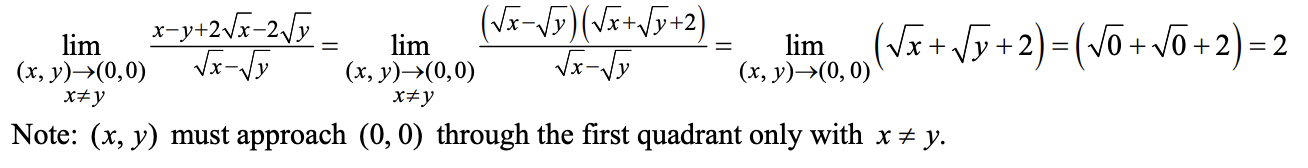
      image-20250408195323100 image-20250408195337227

      • 定理：\(D\subseteq\mathbb R^n\)时，极限存在当且仅当在\(\mathbb R^n\)以任何路径靠近这个点时函数值趋于同一个值。可以用来判断极限是否存在

        例：14.2.47

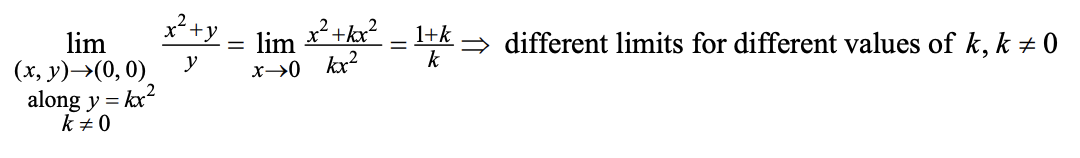
        image-20250408195925016 image-20250408195938326

        例：14.2.50

        image-20250408200039168 image-20250408200052215

    • 双变量函数的连续性：在\(x_0\)连续当且仅当\(lim_{x\to x_0}f(x)=f(x_0)\)，\(f\)连续当且仅当在定义域内任何点连续。连续函数的和、差、积、商、幂都连续

      • 定理：令f为连续的多变量函数，g为连续的单变量函数且f值域在g定义域内，则\(g(f(x))\)在\(D\)连续

    • 偏导数：在一个点处函数值随其中一个自变量的变化率，如\(\frac{\partial f}{\partial x}(x_0,y_0)=lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}h\)

      偏导数通常写作(以y为例)：\(\frac{\partial f}{\partial y},f_y,D_yf,D_2f\)

      \(f_{xy}\)表示\(f\)先对\(x\)求偏导再对\(y\)求偏导的结果，\(\frac{\partial^2w}{\partial x\partial y}\)相反

      • Clairaut’s Theorem(Mixed Derivative Theorem) 混合偏导数定理：若\(f_{xy},f_{yx}\)在\((a,b)\)及其邻域内(因此\((a,b)\)不能在定义域边界)存在且连续，则\(f_{xy}(a,b)=f_{yx}(a,b)\) (这个定理疑似不太重要)

    • 偏导数连续\(\Rightarrow\)可微性\(\Rightarrow\)连续性；类比单变量函数：可微性\(\Rightarrow\)连续性

      双变量函数可微说的就是函数可以在该点用一个切平面近似

      对于各个自变量的偏导数均存在并不意味着连续 例：这个函数\(f(x,y)=0(xy\neq0);1(xy=0)\)，在\((0,0)\)各个自变量的偏导数均存在但不连续

      对于双变量函数，偏导数连续指的是当点(x,y)接近(a,b)时，\(f_x,f_y\)分别接近\(f_x(a,b),f_y(a,b)\)；可微性指的是\(f(a+h,b+k)\approx f(a,b)+h\cdot f_x(a,b)+k\cdot f_y(a,b)\)，也就是\(lim_{(\Delta x,\Delta y)\to(0,0)}\frac{E}{\sqrt{\Delta x^2+\Delta y^2}}=0,E=\)实际值-估计值

    • 判断可微性的另一个定理：\(f_x\)和\(f_y\)在\((x_0,y_0)\)及其邻域存在，且在\((x_0,y_0)\)连续

    • 求导规则

      • \(z=f(x,y),x=x(t),y=y(t)\)，则\(\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y}\frac{dy}{dt}\)

      • 一般地：

        image-20250323133551445

    • 用双变量函数求平面曲线斜率

      \(F(x,y)=0\) 是一条平面曲线，\(\frac{dy}{dx}=-\frac{F_x}{F_y}\)

      例：14.4.28

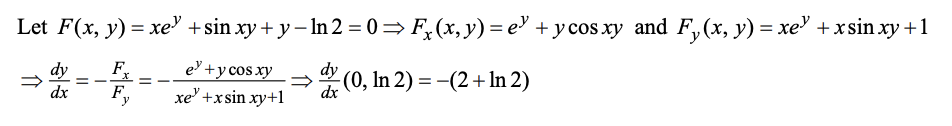
      image-20250324140412733 image-20250324140430609

      扩展到高维同理，如求\(\frac{\partial z}{\partial x}\)：

      image-20250323142252926

    • Directional Derivative 方向导数

      \(u=<u_1,u_2>,||u||=1,D_uf(x_0,y_0)=lim_{h\to0}\frac{f(x_0+hu_1,y_0+hu_2)-f(x_0,y_0)}{h}\)

      令\(\nabla f=<\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}>\)(Gradient Vector，梯度向量；更多变量时梯度向量的计算方式也是类似，即对每个自变量分别求偏导)，则\(D_uf(x_0,y_0)=\nabla f(x_0,y_0)\cdot u\)；易发现\(f,u\)同向时增长最快，反向时减少最快，垂直时无变化

      各个方向的方向导数存在并不意味着可微，例：类似捏着一个点拎起的床单，在该点处不能用一个切平面近似

      • Applications & Tricks

        求一个曲面到另一个平面距离最近/最远的点：是要求出曲面上切面与该平面平行的点

        例：14.7.49

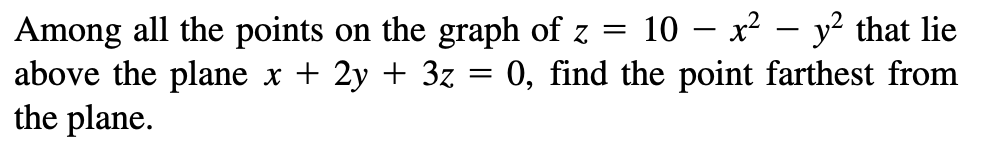
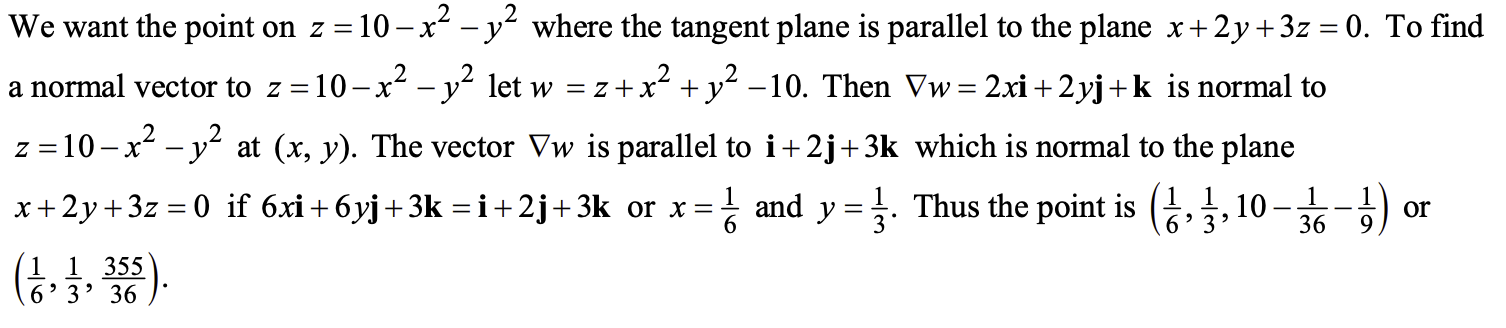
        image-20250401001436377 image-20250401001447901

    • Level Curve 等高线

      \(z=f(x,y)=k\)

      \(\frac d{dt}f(x(t),y(t))=f_x\frac{dx}{dt}+f_y\frac{dy}{dt}=\nabla f\cdot \overrightarrow{r'}(t)=0\)，因此等高线上一点的梯度向量永远与等高线的切线垂直(先用常识理解结论，再看式子)

    • 求解切平面方程

      关键：\(f(x,y,z)=k\)在\((x_0,y_0,z_0)\)处的梯度向量垂直于切平面。可以用上面的"梯度向量永远与等高线的切线"理解(三维曲面是四维空间中的一条等高线)。更严谨的证明：沿\((x_0,y_0,z_0)\)处的任何一个切向量方向，\(f(x,y,z)\)的值变化趋势都为0，由于"\(f,u\)同向时增长最快，反向时减少最快，垂直时无变化"，因此\(f\)垂直于任意一个切向量，因此\(f\)垂直于切平面

      因此：

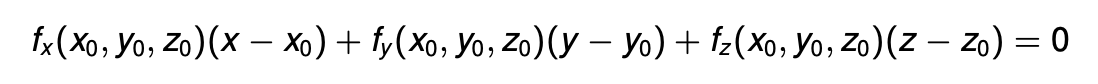
      image-20250323170155392

      例：14.6.8

      image-20250325232408763 image-20250325232420327

      使用切平面对\(z\)进行Tangent Plane Approximation(也就是线性化，Linearization): \(L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)\)，\(E=f(x,y)-L(x,y)\)

      线性化的误差的范围(公式要背):

      1. 双变量的情况
      image-20250323224831425
      1. 三变量的情况
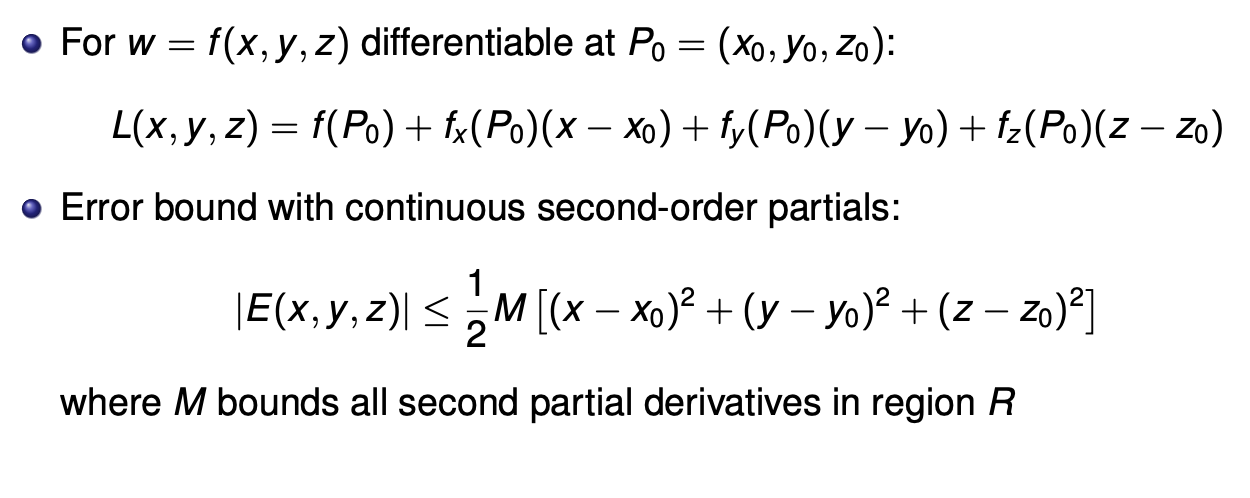
      image-20250323225604567

      例：14.6.36

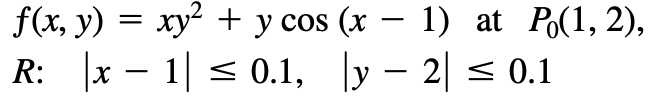
      image-20250326000915497 image-20250326000928423

      • Applications & Tricks

        求两曲面交线在某一点处的切线方程：两者在要求的交点处的梯度向量的叉积即为切线方向向量

        例：14.6.17

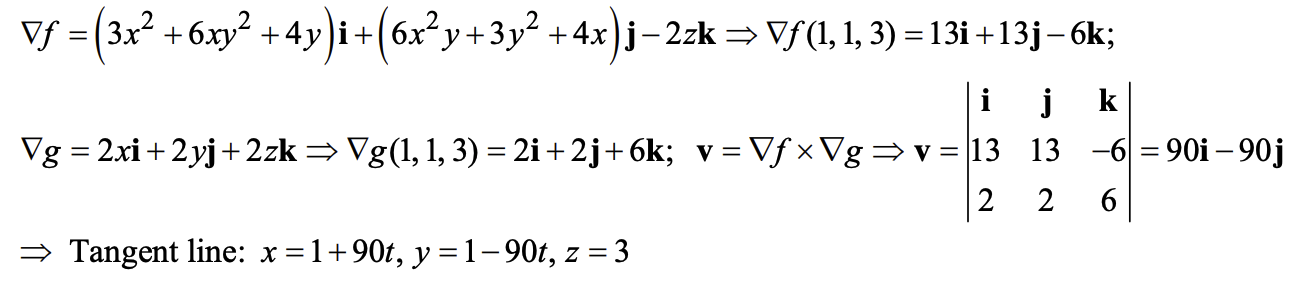
        image-20250325234610810 image-20250325234621416

    • 多变量函数的微分：

      \(dz=df=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy\)

      例：圆柱\(V=\pi r^2h,dV=2\pi rhdr+\pi r^2dh\)

    • 四种"关键位置"

      1. Local(Relative) Extrema 局部极值：函数在某点的值 大于等于 或 小于等于 在其邻域内且在定义域内 的所有的函数值。注意：由于等号存在，常函数中任意一个点都是局部极值点

        辅助判定方法：First Derivative Test

        image-20250323233109124

      2. Critical Point 临界点：所有偏导数都为0或有任意一个偏导数不存在的点

        局部极值点都是临界点，但反之不成立

      3. Saddle Point 鞍点：是临界点但不是局部极值的点

        判定方法(Second Derivative Test Theorem)：

        image-20250323233439035

        \(H=0\)时无法确定

      4. Global(Absolute) Extrema 全局极值：大于等于 或者 小于等于 定义域内所有其他函数值

        若 函数连续 且 定义域封闭且有界，则全局最大最小值一定存在

        定义域封闭且有界情况下的全局极值求解：

        1. 寻找定义域内部的临界点(梯度向量为0)，取最大/最小值
        2. 将边界(可能需要分段)用单一自变量(可能是原有的\(x,y\)等自变量，也可能引入新的自变量来表示原有自变量)参数化，对该变量求导找出其上的最大/最小值；或者用其他方法求出边界上最值
        3. 将以上两个结果取较大/较小值

      高中管全局极值叫"最值"，管局部极值叫"极值"，不要搞混了

    • Lagrange Multiplier System 拉格朗日乘数法：一种用于寻找受约束优化问题中极值点的方法，也就是在定义域为\(g(x,y,\cdots)=k\)(这个定义域是\(f\)原定义域的一个子集)的前提下求\(f(x,y,\cdots)\)的全局极值。使用前提是原函数和约束函数均可微

      比如求双变量函数定义域部分区域上的全局极值：若\(f(x,y)\)在D中可微，\(\overrightarrow r(t)\)是D中的一条曲线，且其上一点\(P_0\)处的函数值是曲线上的全局极值，则\(\nabla f(P_0)\perp {\overrightarrow r}'(t_0)\)。该结论对更多自变量的函数也相应成立。若把这条曲线用\(g(x,y)=k\)表示，则在该全局极值点处，\(\nabla f=\lambda \nabla g\)(因为两个梯度向量都垂直于\(g\)在此处的切线)，其中\(\lambda\)被称为Lagrange Multiplier(可以\(=0\))。例：

      image-20250330212018816

      若约束条件\(g\)不止一个，则限制条件下的全局极值点满足\(\nabla f\)在此处几个\(g\)的梯度向量组成的平面内(或高维平行多面体内)，例：要在\(g_1(x,y,z)=g_2(x,y,z)=0\)的限制条件下找到\(f(x,y,z)\)的全局极值点，则全局极值点满足\(\nabla f=\lambda_1\nabla g_1+\lambda_2\nabla g_2\)。令变量个数为\(n\)，限制个数为\(m\)，则总共有\(n+m\)个方程。拉格朗日乘数法找出的点都是Critical Point

      例：14.8.14

      image-20250401210022469 image-20250401210035528

      例：14.8.46

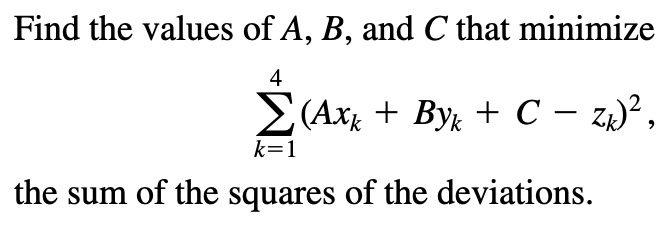
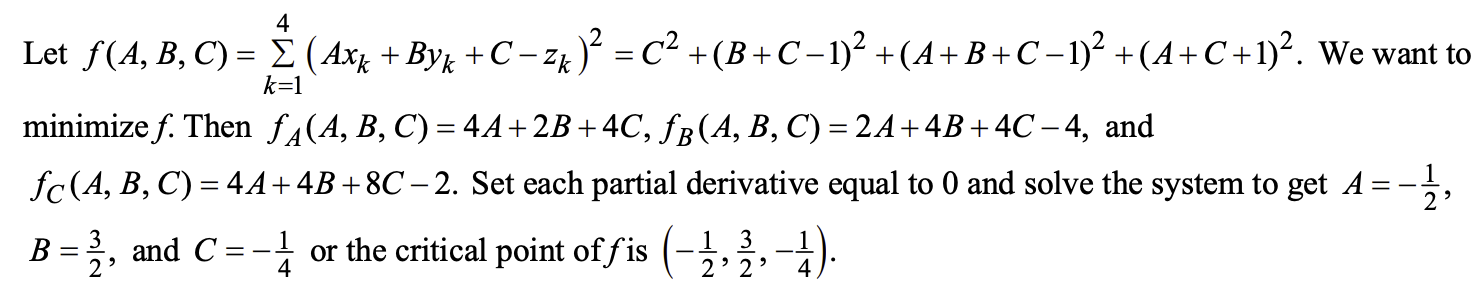
      image-20250401212137156 image-20250401212147841 image-20250401212209057

    • 双变量函数的二次近似：用泰勒展开取一二次项

      \(f(x,y)\approx f(x_0,y_0)+(x-x_0)f_x(x_0,y_0)+(y-y_0)f_y(x_0,y_0)+\frac12 [(x-x_0)^2f_{xx}(x_0,y_0)+2(x-x_0)(y-y_0)f_{xy}(x_0,y_0)+(y-y_0)^2f_{yy}(x_0,y_0)]\)

      例：14.9.4

      image-20250401213828429 image-20250401213845736

  • Functions of Several Variables 多变量函数 积分相关部分

    • 双变量函数图像下的体积计算(双重积分)

      • 若要求体积的区域的底部是一个矩形：

        \(V=\int\int_Rf(x,y)dA=\int_c^d\int_a^bf(x,y)dx\ dy=\int_a^b\int_c^df(x,y)dy\ dx\)，其中\(A\)是一个极小的矩形的面积

        例：15.1.10

        image-20250402202059913 image-20250402202110080

        内外层\(x,y\)的顺序可以随意交换(Fubini's Theorem)

        例：15.1.34

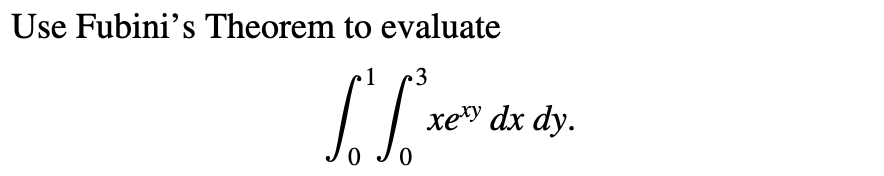
        image-20250402203256165 image-20250402203317901

      • 若底部的其中一维可以用另一维表示，分以下两种情况：

        image-20250401154440060

        用含\(x\)的式子的值限制\(y\)的范围(即内层定积分上下界是用\(x\)表示的)的是Type-I，Type-II则相反

        如果直接计算困难，可以交换\(x,y\)的顺序(Fubini's Theorem)，如\(\int_0^1\int_x^1sin(y^2)dy\ dx\to\int_0^1\int_0^ysin(y^2)dx\ dy\)

      • 若底部是一个圆环的一部分(或是其他适合于转换成极坐标的形状)，则(以圆环为例)：

        当\(a\leq r\leq b,\alpha\leq \theta \leq \beta,x=rcos\theta,y=rsin\theta\)时，\(V=\int\int_Df(x,y)dA=\int_{\alpha}^{\beta}\int_a^bf(rcos\theta,rsin\theta)r\ dr\ d\theta\)

        理解：\(r\cdot d\theta和dr\)分别是一个极小的矩形的长和宽

        记忆：积分的时候多乘一个\(r\)

        若要计算体积的区域的底部用笛卡尔坐标直接表示和计算比较复杂，而其又刚好是一个圆环，则可以转换成极坐标后用这种方法计算

        例：15.4.25

        极坐标积分转笛卡尔坐标积分：

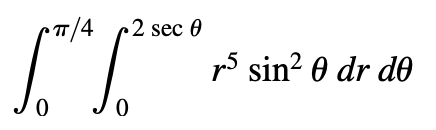
        image-20250405151837902 image-20250405151847529

        例：15.4.36

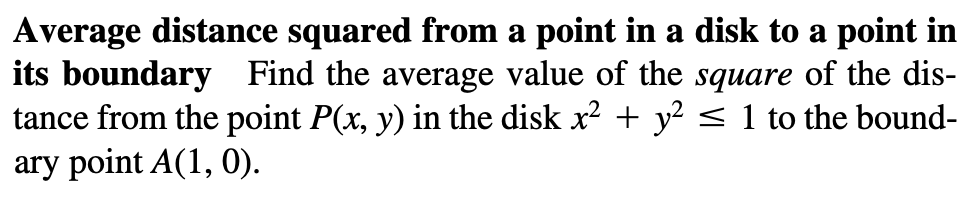
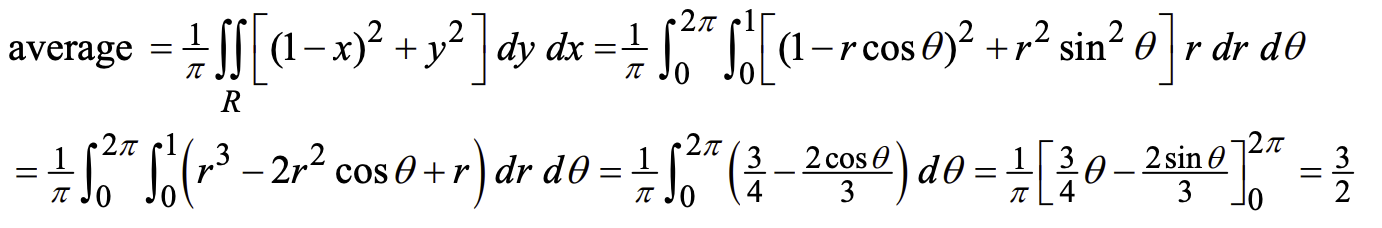
        image-20250405152500384 image-20250405152513311

    • Cylindrical Coordinates 圆柱坐标系：\((r,\theta,z)\)，其中\((r,\theta)\)是在底面上的极坐标，\(z\)是高度

      当底部是适合于转换成极坐标的形状，可以用来简化三重积分的计算，具体来说：

      当\(\alpha\leq\theta\leq\beta,0\leq h_1(\theta)\leq r\leq h_2(\theta),u_1(x,y)\leq z\leq u_2(x,y)\)时，\(\int\int\int_Ef(x,y,z)dV=\int\int_D(\int_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dz)dA=\int_{\alpha}^{\beta}\int_{h_1(\theta)}^{h_2(\theta)}\int_{u_1(rcos\theta,rsin\theta)}^{u_2(rcos\theta,rsin\theta)}f(rcos\theta,rsin\theta,z)dz\ r\ dr\ d\theta\)

      记忆：和上面提到的用极坐标计算双重积分一样，积分的时候多乘一个\(r\)

      例：15.7.14

      image-20250412214747139 image-20250412214802564

      • 关于坐标转换后计算积分需要乘上的系数：General Change of Variable Formula 变量变换公式

        若\(x=g(u,v),y=h(u,v)\)，则\(\int\int_Df(x,y)dA=\int\int_Rf(g(u,v),h(u,v))|J(u,v)|du\ dv\)，其中\(J(u,v)=\begin{vmatrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}\)

        该结论可以推广至更多变量的情况

        变量转换后定积分上下界的确定：把原区域的边界线用新变量表示

        例：15.8.14

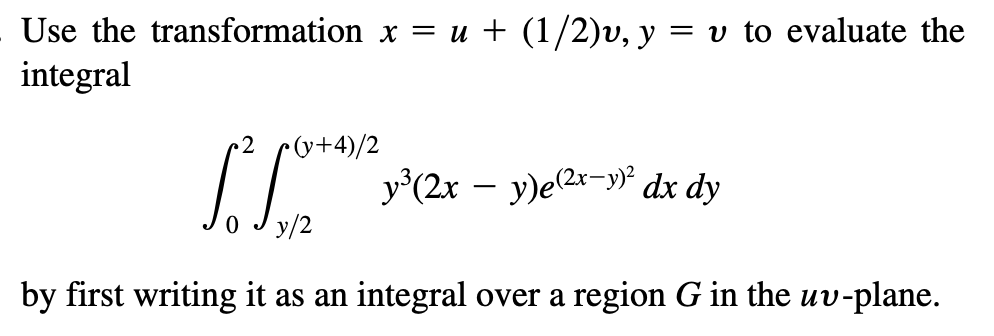
        image-20250412225013301 image-20250412225032404 image-20250412225045182

    • Spherical Coordinates 球坐标系：\((\rho,\phi,\theta)\)，其中\(\rho\)是到原点的距离，\(\phi\)是与\(z\)轴正方向的夹角，\(\theta\)是与\(x\)轴正方向的夹角(\(\rho\geq0,0\leq\phi\leq\pi,0\leq\theta\leq2\pi\))

      image-20250408164359992

      由图知\(z=\rho cos\phi,r=\rho sin\phi,x=\rho sin\phi cos\theta,y=\rho sin\phi sin\theta\)

      \(J(\rho,\phi,\theta)=\rho^2sin\phi\)，可以背下来简化计算

      一般来说球坐标系的积分从内层到外层依次为\(d\rho,d\phi,d\theta\)

      例：15.7.37

      image-20250412222425841 image-20250412222442097

  • Line Integrals (and Surface Integrals) 线积分(和面积分)：

    线积分：\(\int_Cf(x,y,z)ds=lim_{||P||\to0}\sum_{k=1}^nf(x_k,y_k,z_k)\Delta s_k\)

    可以用来解类似这样的问题：空间中有一段绳子，每个部分有不同的密度，求绳子的总质量

    • 求法：\(\int_Cf(x,y,z)ds=\int_a^bf(r(t))||r'(t)||dt\)

      还是很好理解的

    • Vector Field 向量场：是一个形如\(D\to\mathbb R^n\)的函数\(F\)，它为\(D\)中的每个点都分配了一个向量

      动机：粒子在空间中特定的一些位置受到拉力\(F\)，问沿轨迹\(C\)运动过程中，\(F\)做功多少？

      向量场的线积分：\(\int_C F\cdot Tds=\int_a^bF(r(t))\cdot r'(t)dt\)，其中\(T\)是每个位置的单位切向量

      • Applications & Tricks

        对某一个维度求积分，其实就是把上面的内积拆开并对某一个维度单独求

        例：16.2.14

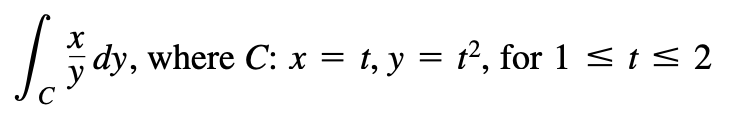
        image-20250413143311357 image-20250413143325916

        求做功多少

        例：16.2.22

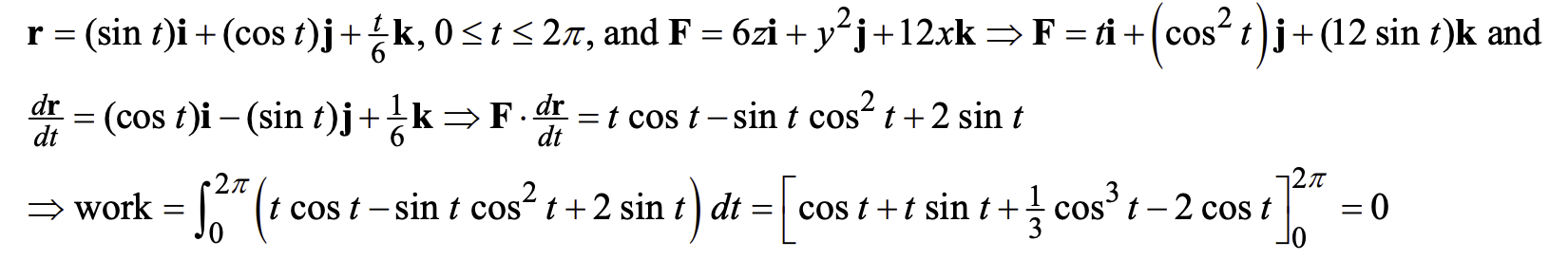
        image-20250413143916673 image-20250413143935478

      有时写作\(\int_CF\cdot dr\)，其中\(dr\)是一个极小的向量

      注意以上几行中的"\(\cdot\)"均表示向量内积

    • Flow Integral 流积分：当\(F\)是一个流体的速度向量场时，其线积分被称为流积分

      若其积分轨迹\(C\)首尾相接，可以写为\(\oint F\cdot Tds\)，这个积分被称为环流(Circulation)

    • Flux 通量

      若\(C\)是一条首尾相接的 简单曲线(Simple Curve，不与自身相交的曲线)，其在每一点处的外单位法向量(\(C\)的边界上指向图形外侧的单位法向量)表示为\(n\)，则其外向通量(Outward Flux)是积分\(\int_CF\cdot n\ ds\)

      这门课中我们提到通量时，指的是外向通量

      外向通量的计算：

      首先，将本问题涉及的所有向量都放到三维空间中(是为了方便计算\(n\))，这一步对结果没有影响

      其次，由下图知\(cn=T\times k(C为逆时针);cn=k\times T(C为顺时针)\)，其中\(k=<0,0,1>,c\)是正常数

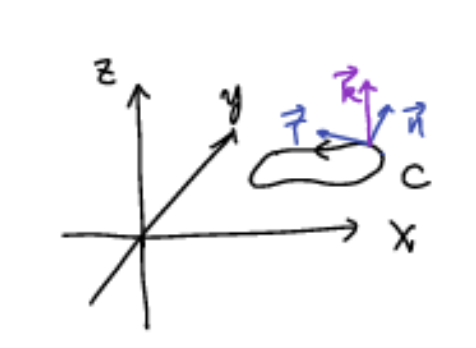
      image-20250412003048198

      经计算，逆时针时\(n=<\frac{dy}{ds},-\frac{dx}{ds},0>\)，顺时针时\(n=<-\frac{dy}{ds},\frac{dx}{ds},0>\)

      若设\(F=<M,N,0>\)，则在逆时针时有\(\int_cF\cdot n\ ds=\oint(M\ dy-N\ dx)\)，顺时针时相反

      最终公式：Flux\(=\int_a^b F\cdot n||r'(t)||dt\)，含有\(||r'(t)||\)是因为把之前的\(ds\)替换成了\(dt\)

      例：16.2.30

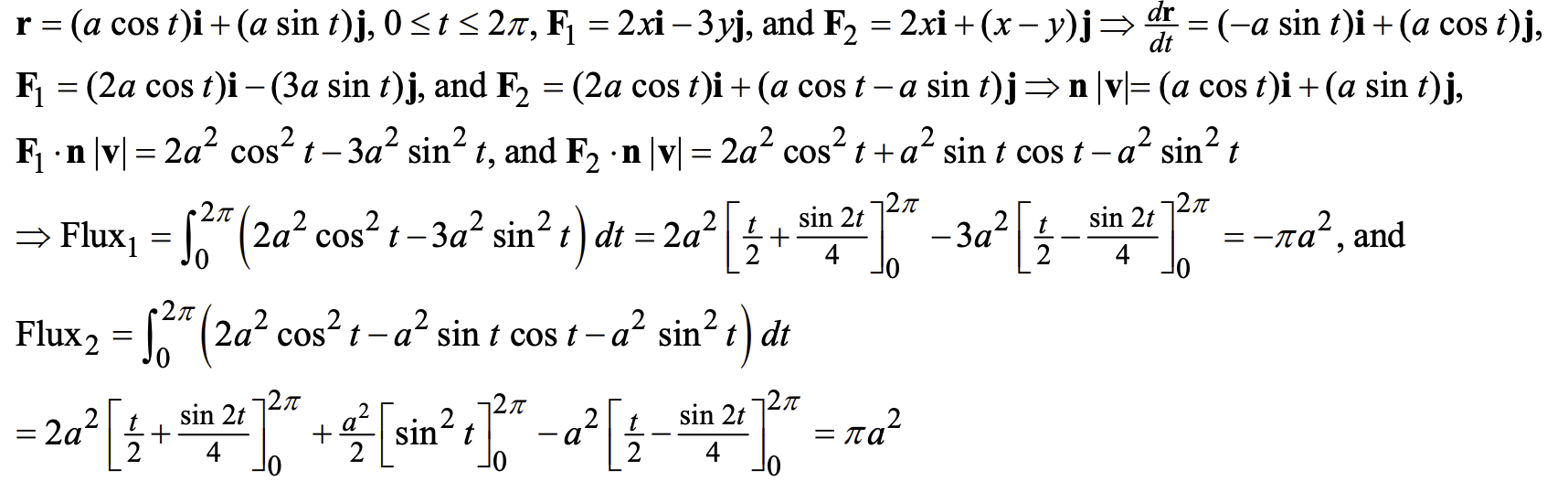
      image-20250413152724752 image-20250413152736315

    • Conservative Field 保守场：任意线积分的值与路径无关，只与起终点有关的向量场。例：垂直向下的重力场

      一个向量场\(F\)是保守场当且仅当\(\forall C,\oint F\cdot dr=0\)，其中\(dr=T\ ds\)

    • 若向量场\(F=\nabla f\)，则\(f\)称为\(F\)的一个势能函数(Potential Function)

      这个起名也很好理解

      例：16.3.10

      Find potential function for F

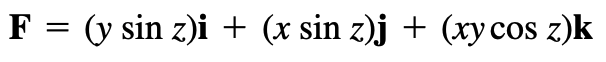
      image-20250416211724984 image-20250416211752800

    • 若向量场\(F\)的各个分量在一个连续的定义域\(D\)上连续，则\(F\)是保守场当且仅当其是一个梯度场(即\(\exist f\ s.t.\ F=\nabla f\))

    • Fundamental Theorem of Line Integrals

      若\(f\)是一个定义域包含轨迹\(C\)的函数，且其梯度向量\(\nabla f\)在一个包含\(C\)的区域内连续，则\(\int_C\nabla f\cdot dr=f(B)-f(A)\)

      因此，"Any continuous gradient field is conservative"

    • Simply Connected Region 简单连通区域：若在一个平面上的连通区域\(D\)满足其中任意一条首尾相接的简单曲线都只包住\(D\)内部的点，则称\(D\)为简单连通区域

      image-20250415181941561

    • Component Test for Conservative Fields 保守场的分量测试

      令\(F\)是简单连通区域\(D\)上的一个向量场，令其为\(<M(x,y),N(x,y)>\)，则其为保守场当且仅当\(\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}\)

      注意：若定义域不是简单连通区域，就算满足这个测试，也不一定是保守场

      在更高维的空间中同样有这个测试，如在三维空间中，\(F=<M,N,P>\)，测试通过的条件为\(\frac{\partial P}{\partial y}=\frac{\partial N}{\partial z},\frac{\partial M}{\partial z}=\frac{\partial P}{\partial x},\frac{\partial N}{\partial x}=\frac{\partial M}{\partial y}\)

      例：16.3.2

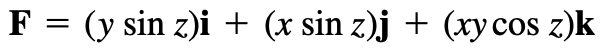
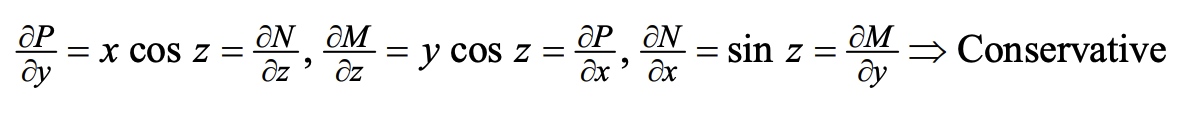
      image-20250416212158177 image-20250416212212400

    • Green's Theorem 格林定理

      令\(C\)为一个简单闭合曲线，\(R\)为其围出的区域，\(M,N\)为定义在平面上的函数且其所有偏导数连续，向量场\(F=<M,N>\)，则对于\(C\)为正定向(也就是所谓"内部区域"在其左侧，这种情况下是沿逆时针方向走)的情况下的环流，有：

      \[\int_CF\cdot T\ ds=\int\int_R(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y})dA \]

      若\(C\)为负定向则相反

      同时，对于\(C\)的(外向)通量，有：

      \[\int_CF\cdot n\ ds=\int\int_R (\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y})dA \]

      有点抽象！！

      理解：

      • 环流的格林定理(以轨迹逆时针为例)

        现断言：若\(dA\)为一个极小的矩形(其长宽分别为\(dx,dy\))，则\((\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y})dA\)为这个矩形边界上的环流

        注意到，若将区域\(R\)分割成若干极小的矩形，则这些矩形边界上的环流之和是\(R\)边界上(即\(C\))的环流，因为两个矩形相邻边界上的环流会相互抵消

        断言的证明(可以画图辅助理解)：令一个极小矩形左下角的坐标为\((x_0,y_0),N_0=N(x_0,y_0)\)。回顾：一段极短的直线的流量是\(F\cdot T\ ds\)。则矩形左侧竖边流量\(C_l=N_0dy\)，右侧竖边流量\(C_r=(N_0+\frac{\partial N}{\partial x}dx)dy\)，注意这两个流量均以\(y\)轴正方向为正方向；由于轨迹逆时针，两条竖边对环流的总增量为\(C_r-C_l=\frac{\partial N}{\partial x}dxdy=\frac{\partial N}{\partial x}dA\)。类似地，两条横边对环流的总增量为\(-\frac{\partial M}{\partial y}dA\)。相加即得原式

      • 通量的格林定理

        现断言：\((\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y})dA\)为这个矩形的(外向)通量

        注意到，若将区域\(R\)分割成若干极小的矩形，则这些矩形的通量之和是\(C\)的通量，因为两个矩形相邻边界上产生的通量会相互抵消

        断言的证明：令一个极小矩形左下角的坐标为\((x_0,y_0),N_0=N(x_0,y_0)\)。回顾：一段极短的直线产生的(外向)通量是\(F\cdot n\ ds\)。则矩形下方横边通量\(F_b=-N_0dy\)，上方横边通量\(F_u=(N_0+\frac{\partial N}{\partial y}dx)dy\)，对通量总增量为\(F_b+F_u=\frac{\partial N}{\partial y}dxdy=\frac{\partial N}{\partial y}dA\)。类似地，两条竖边对通量的总增量为\(\frac{\partial M}{\partial x}dA\)。相加即得原式

      若\(R\)是连通区域但并非简单连通，如下图：

      image-20250417204902678

      此时正定向闭合曲线\(C_2\)的方向是顺时针，而\(C_1\)是逆时针

      因此对于这种类型的\(R\)，仍然有\(\int\int_R(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y})dA=\oint F\cdot T\ ds\)

      对于这种类型的\(R\)，通量的格林定理也有类似的通用公式，只不过为了使公式成立，需要把\(R\)中每个"洞"的边界的外单位法向量(\(n\))定义为指向洞的内部

      例：16.4.8

      image-20250418135935888 image-20250418135951875

    • Parametric Surfaces 参数曲面

      \(r(u,v)=<x(u,v),y(u,v),z(u,v)>,(u,v)\in\mathbb R^2\)

      例：16.5.6

      参数化以下曲面

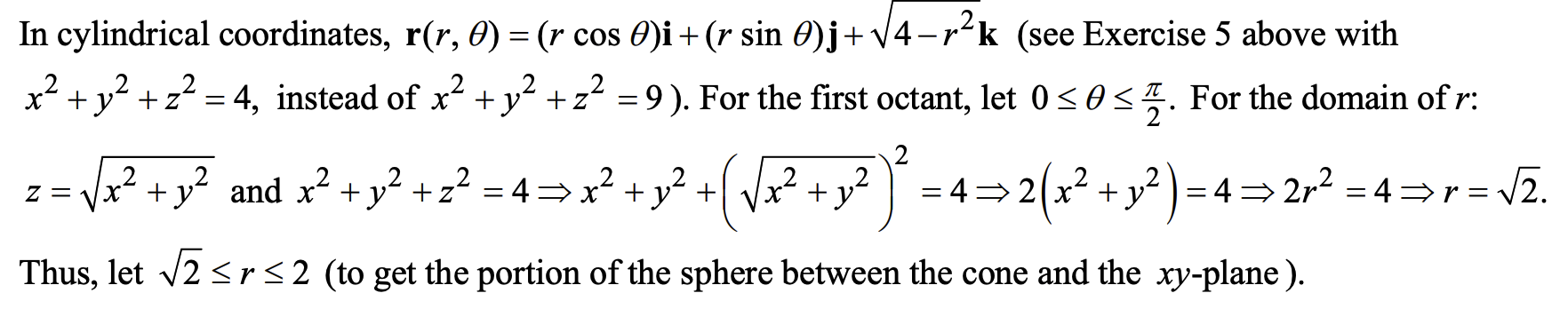
      image-20250418151040322 image-20250418151051850

      • 参数曲面在某点的切面

        令\(P_0=r(u_0,v_0)\)，\(r_v=<(\frac{\partial x}{\partial v})(u_0,v_0),(\frac{\partial y}{\partial v})(u_0,v_0),(\frac{\partial z}{\partial v})(u_0,v_0)>,r_u=<(\frac{\partial x}{\partial u})(u_0,v_0),(\frac{\partial y}{\partial u})(u_0,v_0),(\frac{\partial z}{\partial u})(u_0,v_0)>\)，则\(r_v,r_u\)是曲面在\(P_0\)的两个切向量(想象一下：\(r(u,v)\)是三维空间中被摆放成一定形状的一块布，将\(u=u_0,v=v_0\)两条线在这块布上描出来，则表现为布上被画了两条交叉的曲线；在这两条曲线的交点处，\(r_u,r_v\)分别是沿这两条曲线方向的切向量)，\(r_v\times r_u\)是切面的一个法向量，可以根据法向量求出切面

      • 参数曲面的面积

        回顾：两向量叉积的绝对值是其围成平行四边形的面积

        因此，\(S=\int\int_R |r_u\times r_v|du\ dv\)，其中\(R\)是要统计面积的\(u,v\)的范围

    • Surface Integrals 面积分

      令曲面在一点处的面密度为\(g(x,y,z)\)，则曲面总质量为\(\int\int_R g(r(u,v))|r_u\times r_v|du\ dv\)；若曲面以\(z=f(x,y)\)形式给出，则曲面总质量为\(\int\int_Rg(x,y,f(x,y))\sqrt{f_x^2+f_y^2+1}\ dx\ dy\)(可以先参数化然后用公式推出\(\to r_x\times r_y=<-f_x,-f_y,1>\))

    • Orientable Surfaces 可定向曲面：有两个面的曲面

      比如莫比乌斯环就只有一个面，不是可定向曲面

      本课程只考虑可定向曲面

    • 通量的面积分

      令流体速度场为\(v(x,y,z)\)，则通过可定向曲面的通量积分为\(\int\int_S vn\ d\sigma\)，其中\(n\)为曲面在某一点的单位法向量，\(n=\pm \frac{r_u\times r_v}{||r_u\times r_v||}\)

    • 向量场的旋度(Curl)

      对于向量场\(F=<M,N,P>\)，其旋度为\(curl\ F=<\frac{\partial P}{\partial y}-\frac{\partial N}{\partial z},\frac{\partial M}{\partial z}-\frac{\partial P}{\partial x},\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}>\)，衡量向量场在某点的旋转趋势

      表示方法：\(curl\ F=\nabla\times F\)，其中\(\nabla=<\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}>\)，这个叉积表示方法可以简化向量场的计算并方便记忆

      理解：

      • 令\(curl\ F=<A,B,C>\)，当\(A>0\)时，将右手大拇指指向\(x\)轴正方向，则四指方向是该点向量场在垂直于\(x\)轴平面内旋转趋势的方向(右手定则)；当\(A<0\)时则相应地将右手大拇指指向\(x\)轴负方向得出。对于\(y,z\)方向，也是类似地判断。注意，此时\(xyz\)轴之间的位置关系也符合右手定则，见前文"3D Space"
      • 另一种理解方式：将一个极小的球体放在一个流体的速度向量场\(F\)中，球体会因为摩擦力/粘滞力什么的而开始旋转，其旋转的正轴方向即旋度的方向，旋度大小则衡旋转的速度。正轴方向和旋转方向的关系用右手定则判断，即拇指方向为正轴的方向，四指方向为旋转的方向

      任意点旋度都为0的向量场是无旋(Irrotational)的；在简单连通区域上，无旋向量场与保守向量场等价

    • Stoke's Theorem

      对于有向曲面\(S\)和其边界\(C\)，\(\oint_CF\cdot dr=\int\int_S(\nabla\times F)\cdot n\ d\sigma\)，其中\(n\)是一点垂直于曲面的单位法向量，\(C,n\)的方向关系满足右手定则，即拇指方向为\(n\)的方向，四指方向为\(C\)的正方向

      格林定理的环流形式是该定理在平面上的一个特殊情况

      该定理的理解：类似格林定理，将曲面分成很多小的部分，计算环流总和，其中相邻的部分会互相抵消。点乘单位法向量是为了只留下向量场中与曲面垂直的分量

    • Component Test for 3D Conservative Fields 3D保守场的分量测试

      三维空间中的一个向量场\(<M,N,P>\)在一个简单连通区域中是保守场当且仅当\(P_y=N_z,M_z=P_x,N_x=M_y\)

    • Divergence 向量场的散度：衡量向量场某一点处"源"或"汇"强度的一个标量

      \(div(F)=\nabla\cdot F\)。三维情况下，\(div(F)=\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y}+\frac{\partial P}{\partial z}\)，若其为正，则说明向量场中这个点是一个"源"，也就是它无中生有了一些流量；为负则相反

      • Divergence Theorem 散度定理

        简单来说就是若有一个由曲面\(S\)围成的实心空间(Solid)\(E\)，则\(S\)的外向通量\(\int\int_SF\cdot n\ d\sigma=\int\int\int_Ediv(F)dV\)，还挺好理解的。具体限制见下图

        image-20250426210039759

        若该空间是由若干个光滑的曲面围成，也满足Divergence Theorem

posted @ 2025-04-09 21:22  LegendStane  阅读(1072)  评论(1)    收藏  举报