jixuchongai

导航

 
OO第一单元总结

OO第一单元总结

1、度量分析

1.1第一次作业

1.1.1类复杂度分析

  • OCavg：Average Operation Complexity

  • OCmax：Maximum Operation Complexity

  • WMC：Weighted Method Complexity

classOCavgOCmaxWMC
Poly 5.428571428571429 10.0 38.0
Main 5.0 5.0 5.0
Parser 3.5 5.0 14.0
Lexer 2.5 6.0 10.0
Term 2.0 5.0 8.0
Expr 1.75 4.0 7.0
Number 1.0 1.0 3.0
P 1.0 1.0 4.0
Variable 1.0 1.0 2.0
Total     91.0
Average 2.757575757575758 4.222222222222222 10.11111111111111

1.1.2方法复杂度分析

  • CogC：Cognitive Complexity

  • ev(G)：Essential cyclomatic

  • iv(G)：Design Complexity

  • v(G)：Cyclomaitc Complexity

methodCogCev(G)iv(G)v(G)
Poly.print() 27.0 2.0 9.0 10.0
Poly.add(Poly) 12.0 1.0 8.0 10.0
Poly.sub(Poly) 12.0 1.0 8.0 10.0
Poly.mul(Poly) 11.0 1.0 7.0 9.0
Term.transfer() 9.0 1.0 5.0 5.0
Main.main(String[]) 7.0 3.0 6.0 6.0
Lexer.next() 6.0 2.0 6.0 8.0
Parser.parseExpr() 6.0 1.0 5.0 5.0
Parser.parseTerm() 6.0 1.0 5.0 5.0
Parser.parseFactor() 5.0 5.0 5.0 5.0
Expr.transfer() 4.0 1.0 4.0 4.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Poly.pow(int) 1.0 1.0 2.0 2.0
Expr.Expr() 0.0 1.0 1.0 1.0
Expr.addOp(String) 0.0 1.0 1.0 1.0
Expr.addTerm(Term) 0.0 1.0 1.0 1.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.peek() 0.0 1.0 1.0 1.0
Number.Number(BigInteger) 0.0 1.0 1.0 1.0
Number.getNumber() 0.0 1.0 1.0 1.0
Number.transfer() 0.0 1.0 1.0 1.0
P.P(BigInteger, int) 0.0 1.0 1.0 1.0
P.getC() 0.0 1.0 1.0 1.0
P.getE() 0.0 1.0 1.0 1.0
P.mul(P) 0.0 1.0 1.0 1.0
Parser.Parser(Lexer) 0.0 1.0 1.0 1.0
Poly.Poly() 0.0 1.0 1.0 1.0
Poly.getPs() 0.0 1.0 1.0 1.0
Term.Term() 0.0 1.0 1.0 1.0
Term.addFactor(Factor) 0.0 1.0 1.0 1.0
Term.addOp(String) 0.0 1.0 1.0 1.0
Variable.Variable() 0.0 1.0 1.0 1.0
Variable.transfer() 0.0 1.0 1.0 1.0
Total 108.0 41.0 93.0 102.0
Average 3.272727272727273 1.2424242424242424 2.8181818181818183 3.090909090909091

1.1.3UML类图

 

 

 

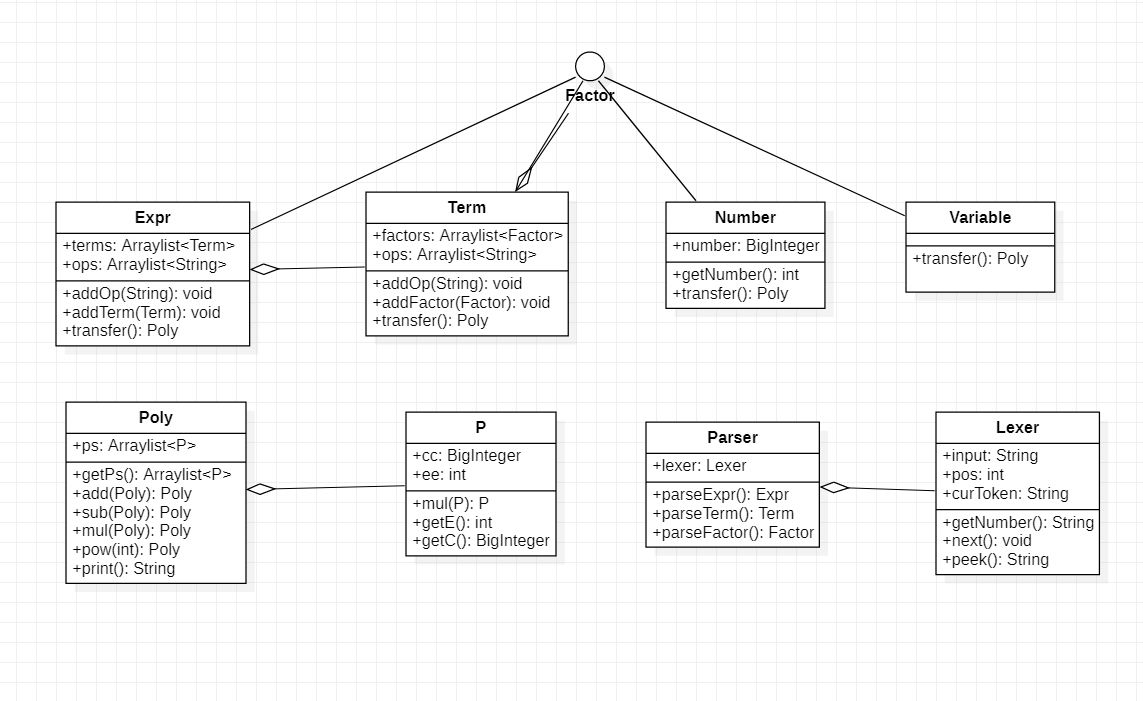
1.2第二次作业

1.2.1类复杂度分析

classOCavgOCmaxWMC
Unity 4.75 14.0 57.0
Processor 4.6 8.0 23.0
Parser 4.0 7.0 16.0
Lexer 3.5 10.0 14.0
Poly 2.25 6.0 27.0
Term 2.25 6.0 9.0
Main 2.0 2.0 2.0
Expr 1.75 4.0 7.0
Cos 1.6 3.0 8.0
Sin 1.6 3.0 8.0
Power 1.2 2.0 6.0
Number 1.0 1.0 3.0
Variable 1.0 1.0 2.0
Total     182.0
Average 2.757575757575758 5.153846153846154 14.0

1.2.2方法复杂度分析

methodCogCev(G)iv(G)v(G)
Unity.equals(Unity) 45.0 14.0 12.0 18.0
Unity.print() 33.0 3.0 15.0 15.0
Unity.printCoss(int) 21.0 1.0 8.0 8.0
Unity.mul(Unity) 18.0 7.0 11.0 11.0
Processor.replaceSum() 17.0 1.0 7.0 8.0
Term.transfer() 14.0 1.0 7.0 7.0
Poly.print() 13.0 2.0 5.0 6.0
Lexer.next() 12.0 2.0 11.0 12.0
Processor.replaceSelf(char) 11.0 1.0 6.0 7.0
Poly.add(Poly) 8.0 4.0 5.0 5.0
Parser.parseFactor() 7.0 7.0 7.0 7.0
Parser.parseExpr() 6.0 1.0 5.0 5.0
Parser.parseTerm() 6.0 1.0 5.0 5.0
Cos.Cos(String) 4.0 1.0 3.0 3.0
Expr.transfer() 4.0 1.0 4.0 4.0
Processor.removeBlank(String) 4.0 1.0 4.0 4.0
Sin.Sin(String) 4.0 1.0 3.0 3.0
Poly.move() 3.0 3.0 3.0 3.0
Poly.mul(Poly) 3.0 1.0 3.0 3.0
Power.equals(Power) 3.0 2.0 2.0 3.0
Processor.Processor(String, HashMap) 3.0 1.0 4.0 4.0
Unity.add(Unity) 3.0 3.0 3.0 3.0
Cos.equals(Cos) 2.0 2.0 1.0 2.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Sin.equals(Sin) 2.0 2.0 1.0 2.0
Main.main(String[]) 1.0 1.0 2.0 2.0
Poly.negate() 1.0 1.0 2.0 2.0
Poly.pow(int) 1.0 1.0 2.0 2.0
Cos.getCo() 0.0 1.0 1.0 1.0
Cos.getExp() 0.0 1.0 1.0 1.0
Cos.transfer() 0.0 1.0 1.0 1.0
Expr.Expr() 0.0 1.0 1.0 1.0
Expr.addOp(String) 0.0 1.0 1.0 1.0
Expr.addTerm(Term) 0.0 1.0 1.0 1.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.peek() 0.0 1.0 1.0 1.0
Number.Number(BigInteger) 0.0 1.0 1.0 1.0
Number.getNumber() 0.0 1.0 1.0 1.0
Number.transfer() 0.0 1.0 1.0 1.0
Parser.Parser(Lexer) 0.0 1.0 1.0 1.0
Poly.Poly() 0.0 1.0 1.0 1.0
Poly.addUnity(Unity) 0.0 1.0 1.0 1.0
Poly.clearUnities() 0.0 1.0 1.0 1.0
Poly.getUnities() 0.0 1.0 1.0 1.0
Poly.setUnities(ArrayList) 0.0 1.0 1.0 1.0
Poly.sub(Poly) 0.0 1.0 1.0 1.0
Power.Power(BigInteger, int) 0.0 1.0 1.0 1.0
Power.getCo() 0.0 1.0 1.0 1.0
Power.getExp() 0.0 1.0 1.0 1.0
Power.mul(Power) 0.0 1.0 1.0 1.0
Processor.toString() 0.0 1.0 1.0 1.0
Sin.getCo() 0.0 1.0 1.0 1.0
Sin.getExp() 0.0 1.0 1.0 1.0
Sin.transfer() 0.0 1.0 1.0 1.0
Term.Term() 0.0 1.0 1.0 1.0
Term.addFactor(Factor) 0.0 1.0 1.0 1.0
Term.addOp(String) 0.0 1.0 1.0 1.0
Unity.Unity(Power, HashMap, HashMap) 0.0 1.0 1.0 1.0
Unity.getCo() 0.0 1.0 1.0 1.0
Unity.getCoss() 0.0 1.0 1.0 1.0
Unity.getExp() 0.0 1.0 1.0 1.0
Unity.getPower() 0.0 1.0 1.0 1.0
Unity.getSins() 0.0 1.0 1.0 1.0
Unity.negate() 0.0 1.0 1.0 1.0
Variable.Variable() 0.0 1.0 1.0 1.0
Variable.transfer() 0.0 1.0 1.0 1.0
Total 251.0 105.0 182.0 195.0
Average 3.803030303030303 1.5909090909090908 2.757575757575758 2.9545454545454546

1.2.3UML类图

 

 

 

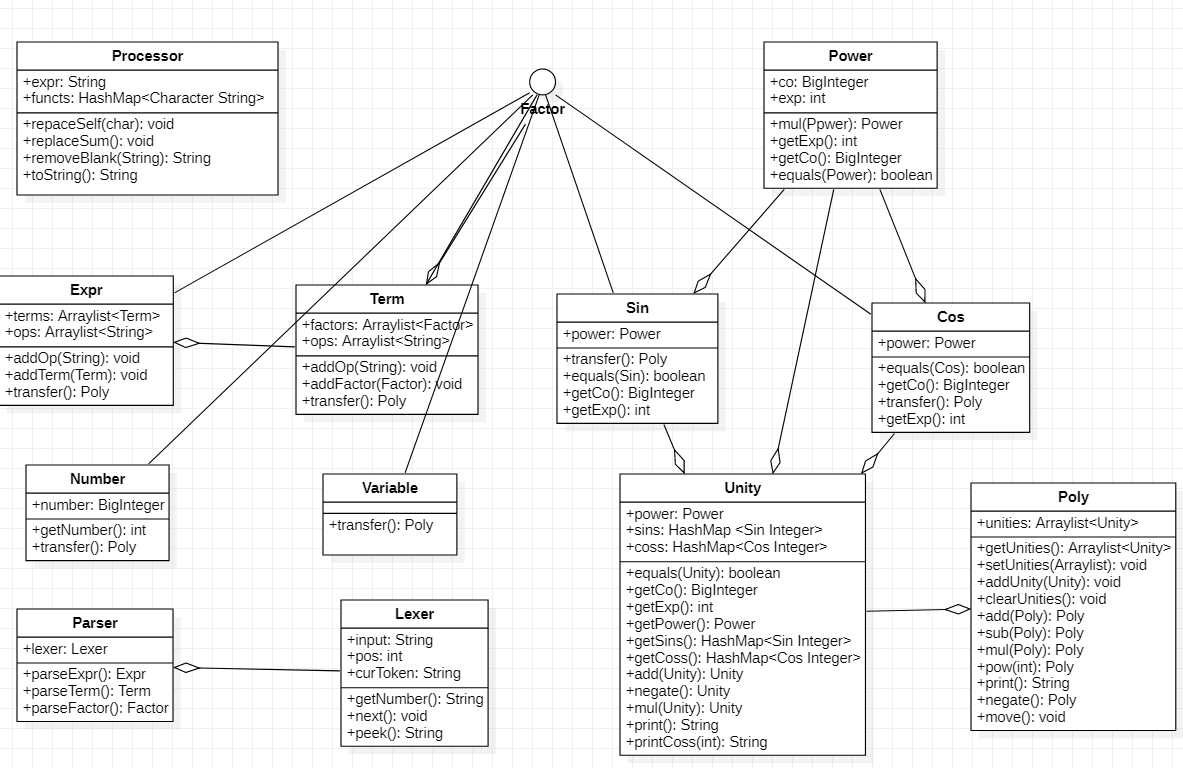
1.3第三次作业

1.3.1类复杂度分析

Parser4.211.021.0
Unity 4.153846153846154 14.0 54.0
Self 4.0 11.0 32.0
Lexer 3.5 10.0 14.0
Poly 3.0 8.0 51.0
Main 2.5 3.0 5.0
Term 2.2 6.0 11.0
Expr 1.8 4.0 9.0
Sum 1.5 3.0 6.0
Variable 1.3333333333333333 2.0 4.0
Cos 1.125 2.0 9.0
Sin 1.125 2.0 9.0
F 1.0 1.0 1.0
G 1.0 1.0 1.0
H 1.0 1.0 1.0
Number 1.0 1.0 4.0
Power 1.0 1.0 4.0
Total     236.0
Average 2.5376344086021505 4.764705882352941 13.882352941176471

1.3.2方法复杂度分析

由于第三次方法较多，仅展示比之前两次迭代开发与较复杂的部分

 

 

 

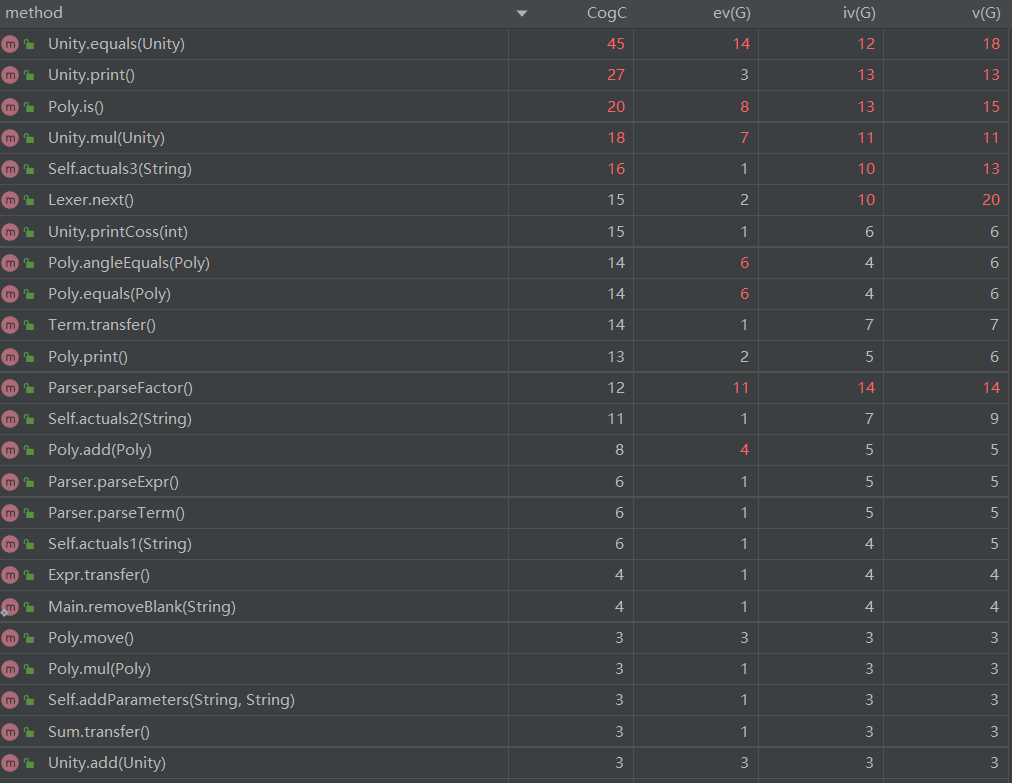
1.3.3UML类图

 

 

 

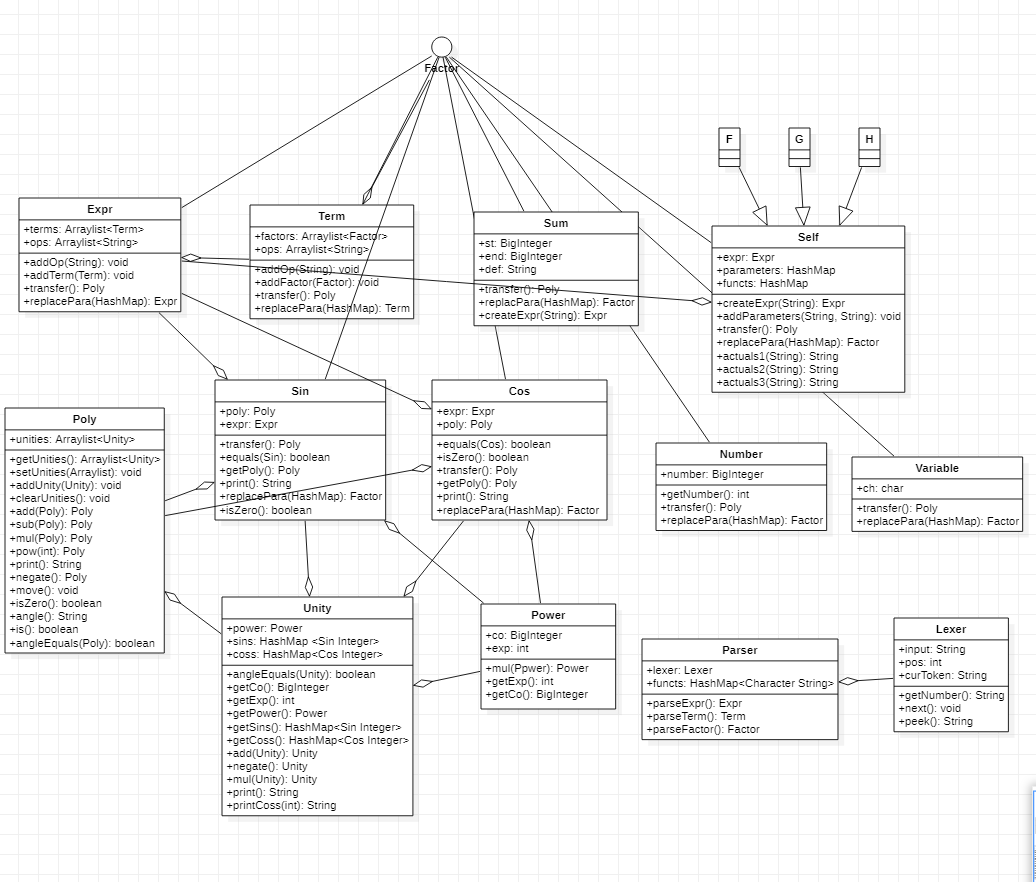
关于软件复杂度度量方法，郭鸿宇同学的博客开头给出了比较详尽的解释

https://www.cnblogs.com/hyguo-blog/p/16043795.html

2、bug与hack分析与反思

2.1自身bug分析

笔者第一次作业强测与互测未出现bug，第二次作业强测出现一个bug，第三次作业则强测与互测都出现了一个共同的bug

为什么三次作业bug越来越多？笔者反思如下：

  1. 强测做的不到位

第一次第二次作业，笔者均未使用强测。对于第一次作业简单的结构与幂函数而言，仅凭中测数据与简单手动构造似乎就可满足正确性的需求。但第二次因情况变得显著复杂，加之笔者采用了易出错的字符串替换方法，故很容易因考虑情况不周和替换方法本身的问题出现错误。

笔者第二次出现的bug是，在直接替换时，出现了诸如x**3**2这种非法字符串形式。合法的字符串不会出现两个乘方符号连续出现的形式，故应该先计算后面的乘方再与前面相乘。而替换后的非法格式会使结果从x**6变成9*x

反思：无论采取何种架构做何种难度的作业，都应针对输入情况进行全方位的测试，才能尽可能避免错误的产生。

  1. 仅依赖强测，未考虑其他情况

笔者第三次作业进行了各种情况的强测，但仍出现了一个输出格式错误。原因在于，常见的导出jar包使用equals比较表达式值的方法，只能检验结果的正确性，却无法检验输出格式的合法性。

而笔者的bug就出现在优化上。若三角函数括号内表达式仅有一项、且该项系数为1，仅有一个幂函数或三角因子时，根据文法规则便可不输出括号。但笔者误多加了一个绝对值，导致系数为-1时也不会输出括号。

反思：仅依靠强测的覆盖性测试是不够的，用课程组一直强调的话来说，”测试不出bug不代表程序的完全正确性“。严格意义上讲，只有通过阅读代码验证逻辑，才能确保最终的正确性。此外，对于各种特殊情况也应考虑周全。

2.2hack策略分析

笔者第一次未发现其他人的bug，后两次可能因自己强测分数不高导致能hack出差不多分数的同房人的bug？（bushi）

综合分析三次hack的经验，总结如下：

  • 做优化时要考虑算法的时间复杂度。有同学为了追求最大限度的优化，采用了贪心比较的优先队列，即：对于二倍角、平方和、提取负号等各种优化都进行一次，然后将结果进行比较最后再输出。这样虽能带来优化的最大化，但必然会导致时间复杂度增加。合理的方法是使用熔断机制等等

例：第三次hack使用了sin(sin(sin(sin(sin(sin(sin(sin(-1))))))))这一数据hack，房间里一位同学因提取负号的算法复杂度过高导致十多秒才完成

  • 对题意的解读。题目中说常数是”有符号允许有前导零十进制数”，但未明确数据规模，许多同学其他因子处理时使用了BigInteger，但求和函数因子却忽略这一点导致出错。

例：第三次hack使用了sum(i,2147483648,0,i)数据hack，可以轻松爆int

  • 字符串替换以及优化时的多种情况。最常见的便是负号处理，直接替换可能带来符号错误。此外，提取三角因子内部符号的优化可能也会导致符号错误。

例：第三次使用sum(i,-1 , 3, i**2) 第二次使用sin(-x)**2,同学都错把加法弄为减法

此外，hack环节应该综合自动化测试、手动构造与阅读他人代码。毕竟hack的宗旨就在于，阅读他人代码，提升逻辑分析能力，同时在此过程中交流借鉴优秀架构与算法。

笔者在第三次hack时有一个关于cost的有趣（sangxinbingkuang）的研究，虽然由于基准展开思路的限制没能使用，不过也在此过程中更深刻体会到了互测限制对大家的保护以及控制时间复杂度的重要性。篇幅所限，放在最后

3、迭代开发与架构设计体验

核心：三次作业的迭代开发是一个整体的过程，迭代的过程逐渐加深了笔者对于架构设计的重要性的认识，建立起解析与计算两套数据结构，也帮笔者逐梳明晰了解析-计算-输出整个过程

3.1HW1

第一次接触到这么大的作业时可以说毫无头绪，幸好教程中有递归下降的训练课程以及吴佬给出的参考代码。在教程的启发下，笔者对“递归下降”有了一个浅显的理解：不同于常规递归的直接调用，递归下降通过模块间的相互协作与引用来实现“递归”的效果，并实现表达式的解析

关键点：

  • 递归下降：解析时，作者借鉴了与教程相同的方式，采用表达式-项-因子三级结构，使用了lexer词法转换器分析文法，parser解析器利用lexer解析整个表达式并将各项、因子解析存储，这是三次作业解析部分的基础

  • 多项式统一处理：在解析后，如何计算的问题卡了我很久，因为各种情况实在太多。对于多种多样的情况，最好的方法便是略过他们的差异性，进行统一处理。

    就像把常数、变量、表达式统一为“factor”一样，对于表达式、项、因子三级结构我均转化为多项式统一处理运算，并在多项式类中引入加减乘以及乘方三级运算。这构成了三次作业运算的基础。

3.2HW2

如果说第一次作业是从0到1，那么第二次作业就是从1到10，处理情况数量陡增。为了应对三角、自定义与求和因子，必须引入更复杂的结构

关键点：

  • 字符串替换：对于自定义函数与求和函数，由于第二次作业不需要递归调用，我采用了字符串替换的方法，把两者直接替换为相应的表达式字符串后再交给parser进行解析

  • unity统一体架构：第二次作业最终的形式中，最终输出结果的每一项都是这样的：系数-指数-sin组-cos组，为了统一处理，我引入了unity类，其包含系数、x的指数，以及sin与cos的hashmap。

    为什么是hashmap呢？因每个三角因子都有耦合的三角函数本身和其指数，所以必须采用以三角类为key的hashmap才能统一处理。相应的，多项式类内部的动态数组也从power幂函数变成了unity统一体

  • 运算：乘法可以直接分块进行，对幂函数、sin与cos部分分别进行乘法，通过重写并调用幂函数的equals方法判断，若角度相同就指数相加；而加减法时同样需要判断三角函数的hashmap是否全相等。由此看出，equals方法同样需要递归调用

3.3HW3

在我的理解来看，第三次作业实现一个功能的完全开发，递归不仅出现在解析中，更要使用于计算与解析两步

关键点：

  • 自定义函数的处理：向内部传递形参实参一一对应的hashmap，开辟了一个新方法用于形式参数的替换，但是用一个表达式树来替换因子，而非字符串间的替换，这样处理抽象化程度更高，也不必再拘泥于字符串具体的种种限制

    由于调用是递归的，那么替换以及计算也是递归的。为了处理这种递归式的替换，笔者将形参中的x全部替换为w，这样x就变为一个纯粹的实参。在变量类当中，如果判断是w、y、z便会继续替换，而x代表递归的终点，这样实现较为直观

  • 三角函数内部处理：因三角函数内部也可能嵌套自定义、求和与三角因子，故三角函数的角度也从幂函数变成了多项式——为什么不是表达式呢？

    如前文所提，笔者采用了两套数据结构。表达式是解析时的结构，而多项式才是最终计算结果时的结构。为了便于运算与化简，冗长的表达式必须经计算化简为多项式后才可以进行处理

    这样实现意味着计算也需要递归：表达式中包含三角因子，三角因子内部又包含表达式以及多项式，通过递归的加减乘运算实现化简

  • 输出的处理：鉴于三角因子与表达式的相互包含与调用，输出也需要递归的方法，先输出“sin(”，再调用多项式的输出方法。为了避免不必要的括号，又单独引入前文所述方法判断（导致了sin(-x)的bug）

  • 直接调用之前的结构，如解析时直接解析w、y、z，将其归为变量类；又如自定义函数的实参代入，因实参可能是表达式，故将其统一处理为表达式因子，再利用与解析方法相似的表达式-项-因子三级结构代入替换。这样避免了大规模重构，但缺点就在于模块间耦合性增强

4、心得体会

  • 代码风格：课程组最初引入checkstyle量化评判代码风格的方法让笔者觉得非常麻烦。然而当笔者后来进行其他编程因不检查代码风格而感到难受时，良好代码风格的必要性立刻显现出来了：

    有英文意义的驼峰命名让变量的作用变得通俗易懂，无需费力猜测；必要的空格和空行的引入让代码阅读起来更加整齐和清爽；避免单独过长的方法让程序变得更加易于维护......对于工程级别的多人协作开发，只有良好的架构才能保证团队合作的效率

  • Java编程思想：Java有继承、多态、封装三大思想。这次作业中，引入“factor”这一接口，让所有的因子继承它就体现了继承多态的优势：我们在因子层面不关心它到底是哪一种以及具体实现，而仅是把它抽象为项的一个组分，最终的实现放在各个类中。这样可以使层次分类更加清晰

    此外，模块间的协作与调用也很好体现了面向对象的优势。如果利用面向过程来实现本次作业，则需要考虑到过多的细节，调用过多的函数。而采用面向对象的方法时，我们仅需要把整个过程抽象为解析、计算、输出这几个大的部分，具体实现交给下面的类。这样可以很方便的完成较大的任务

  • 模块化与层次化：模块化层次化封装的思想与计组有异曲同工之妙，把功能与属性高度相关耦合的一系列变量组成为一个类，具体处理只在内部的方法实现，对外仅保留一个接口，这样可以有效实现“高内聚、低耦合”的设计思想。从函数到CPU部件再到对象，可以说封装贯穿于编程乃至整个计算机科学的学习

    就像助教学长们针对优化时提到的，良好的架构应该是正确性与优化分开，以实现低耦合性，方便调试，这也是模块化优势的体现

  • 构思与设计并行：对于一个大的工程，应该首先对之有一个整体的构思后再进行，但想一蹴而就明白全部细节后再去按图索骥是不可能的。只有先实现部分构思，才能在写代码的过程中加深对整个过程的理解，再进一步去构思与实现。换言之，这是一个两条腿走路的过程，只迈左脚和只迈右脚都是行不通的

 

第一单元作业到此告一段落了。感谢这个过程中同学与学长的帮助，仅凭自己很难完全驾驭整个过程的实现与调试。希望电梯月自己可以继续克服困难，做好测试，不要强测再寄掉

 

附：关于hack的一个有趣的研究

笔者在第三次互测时，发现房间里一位同学因为优化做的不好，在处理求和函数以及负数的幂函数运算时处理的很慢。其他人的程序半秒内就能跑出的结果，他需要二十秒。为了想要hack他，笔者进行了测试数据的改进。

让我们先阅读互测规则：

  • 输入表达式的有效长度至多为 50 个字符。其中输入表达式的有效长度指的是输入表达式去除掉所有空白符后剩余的字符总数。（本条与公测部分的限制不同）

  • 除此之外，为了限制不合理的 hack，我们要求输入表达式的代价：Cost(Expr) <= 100000

    ，其中表达式代价的计算方法如下

    • Cost(常数) = max(1, len(常数))

    • Cost(x) = 1

    • Cost(a ** b)= Cost(a)^max(b, 1) * max(b, 1) + 2

    • Cost(+a) = Cost(-a) = Cost(a) + 1

    • Cost(sum(i, s, e, t)) = max(Cost(s), Cost(e)) * max(1, e - s + 1) * Cost(t)

  • 满足上述要求后，我们会用官方的基准思路程序对输入数据进行检验，输出有效长度不超过 1000 的视为合法互测数据。（本条与公测部分的限制不同）

笔者开始以为是求和函数的问题，根据sum的cost公式，其由三部分决定：数字长度n、上下界的差值以及求和表达式t的cost。为了hack出TLE，笔者采用的求和表达式是幂函数。

根据幂函数的cost公式，当指数增加时，整个cost会急剧增加。为了避免这一情况，底数cost（a）必须为1，故底数只能为i。这样整个幂函数的cost的复杂度就会从指数级变成b+2，即与指数b成线性关系

而由于表达式的幂函数本质上是乘法的循环，因此幂函数的计算时间也是与指数成线性关系的

因此我们得到结论：运行时间与上下界之差以及指数都成线性关系

而对于求和函数，在上下界s与t数字位数n一定时，上下界差值最大约为10^n，故cost可近似为cost（sum）=n*10^n*cost(t),又有求和表达式t是幂函数i**b，故整个式子cost近似为n*10^n*b。由我们上文的结论，程序运行时间近似为10^n*b，为了实现cost一定时间越长，即时间一定cost越小，n必须为1

但笔者又发现该程序处理底数为正数的幂函数计算很快，故必须引入负数，因此 max(Cost(s), Cost(e))便至少为2了，故笔者设计了sum(i,-9,9,i**2500)的数据，其cost为max(Cost(-9), Cost(9)) * max(1, 9 - （-9） + 1) * Cost(i**2500)`，结果为95076，小于100000的cost限制。

但交上去发现不合法！回去又看限制，笔者发现：我们会用官方的基准思路程序对输入数据进行检验，输出有效长度不超过 1000 的视为合法互测数据！！

笔者此时又发现，同一个式子用求和函数算和直接计算时间差不多，问题应该只在于幂函数，而非求和函数。但若直接采用如(-1)**1000的形式，cost会变成2^1000，故笔者使用sum(i,-1,-1,i**1000)，这个数据可以正好使运行时间超过10秒，cost仅为2004,但按照基准思路去展开后，式子会是（-1）*（-1）*（-1）*……*（-1），长度为3999超过了1000的限制，故最终还是hack失败了

虽然这个hack用例本身意义不大，但笔者通过这个有趣的过程深入了解了互测规则，也切身体会到了控制优化时间复杂度的重要性，以及如果互测限制不够的话，会出现多么优秀（sangxinbingkuang）的hack用例

posted on 2022-03-26 12:59  继续宠爱  阅读(67)  评论(1)  编辑  收藏  举报
 
Powered by:
博客园
Copyright © 2024 继续宠爱
Powered by .NET 8.0 on Kubernetes