树状数组

树状数组

树状数组的一个功能：在 \(nlog_n\) 的时间内，完成单点修改与区间求值。如果用朴素算法求解，修改一个数后，我们还要遍历这个区间，设修改 m 次，时间复杂度为 \(n^2\) 。时间显然相差很多吧。

知识储备 lowbit()

先不考虑这玩意儿干什么用的。想一下，如何求一个二进制数最末尾 1 与后面二进制数所组成的数（也就是1 这一位上的二进制值）。比如是 1010100，求出来是 \((0000100)_2\)，也就是4。

我们只要取他的反码，得到 0101011，再加 1。得到0101100，再将该数与原数按位 与（&），就能得到 0000100。

那为什么这一顿操作就能得出值了呢？简单思考一下，取反之后，从左边看起，0 变为 1， 1 变成了 0。再对这个数加 1，因为要进位，原先的 0 ，现在的 1变成 0，直到遇至第个位 0（原先是 1） 也变回 1，后面的数就不再进位了是吧。可以自己想一遍。再按位 与，后面没有进位的数都变成 0，前面的不就是答案吗。

计算机中取反加 1，其实就是这个数的负数形式。所以代码是这样的

int lowbit(int x)
{
	return x&(-x);
}

思想以及实现

求区间和，很容易想到前缀和对吧。但是这组数是在变化的，所以我们要维护这个区间，这时就要用到树这一结构。因为树的查询很快，\(log_n\) 实现。

一棵普通的树是这样的。

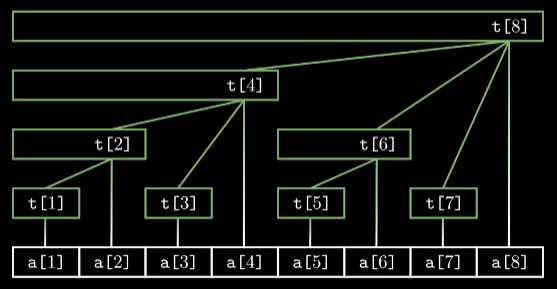
但是树状数组我们可以将其变形为这样。

可以观察到 t_1 管理 a_1; t_2 管理 t_1, a_2; t_3管理 a_3; t_4管理t_2,t_3,a_4。虽然没什么规律，但是我们还是可以注意到：t_i，必定管理a_i。那么其他数字有什么规律呢？

我们上面说了lowbit的用法。如果把每个数的lowbit计算出来，可以发现每个数字的lowbit与他管理个数相同。

直接前驱与直接后继

直接前驱

既然 t 的管理区间与lowbit相同，那我们直接看它的管理区间吧。

还是这张图。7 管理区间为1，它的前驱就是7 - 1 = 6. 6 管理区间是 2 前驱就是6 - 2 = 4.前驱求出来有什么用呢？可以发现 7 与所有前驱加起来就是 a_1 到 a_7 的区间和。那就很方便能求一个区间，前缀和就能够实现了吧。

直接后驱

同样是管理区间。7 的管理区间为 1，直接后继是 7 + 1 = 8。2 的管理区间是 2 ，直接后继就是 2 + 2 = 4.仅举几例。求出直接后继后。我们可以做到修改，维护区间。因为假如把 t_1改变了，他的后继t_2, t_4, t_8 也会改变。

还有要注意的一点：树状数组不能从 0 开始命名，因为lowbit(0) = 0,0 - 0 = 0。会死循环。

代码

#include<iostream>
using namespace std;

#define N 500010

int n, m, t[N];
int u, v, w;

int lowbit(int x)
{
    return x&(-x);
}

void add(int k,int x)
{
    while(k <= n)
    {
        t[k] += x;
        k +=lowbit(k);
    }
}

int query(int x)
{
    int ans = 0;
    while(x > 0)
    {
        ans += t[x];
        x -= lowbit(x);
      
    }
    return ans;
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        int num;
        cin >> num;
        add(i, num);
    }

    for(int i = 1; i <= m; i ++)
    {
        cin >> u >> v >> w;
        if(u == 1)
            add(v, w);
        else
            cout << query(w) - query(v - 1) << endl;
    }
    return 0;
}

看着代码打一遍就差不多会了的。(O…O)

2022-6-6 14:24:24