Luogu P1351 [NOIP2014 提高组] 联合权值 题解

很妙的一道题（吧？

假如我们对于每一个\(i(1\leq i \leq n)\)，都计算出\(i\)和某一个距离相差为\(2\)的\(j\)的联合权值，大概是这样一个代码：

void dfs(int fa,int st,int x,int cnt){
	if(cnt==2){
		mx=max(mx,w[x]*w[st]); 
		sum+=w[x]*w[st];
		sum%=mod;
		return ;
	}
	for(int i=0;i<G[x].size();i++){
		int u=x,v=G[x][i];
		if(v!=fa){
			dfs(u,st,v,cnt+1);
		}
	}
}

我们观察到，如果给的图像这样的形状，就会被卡满：

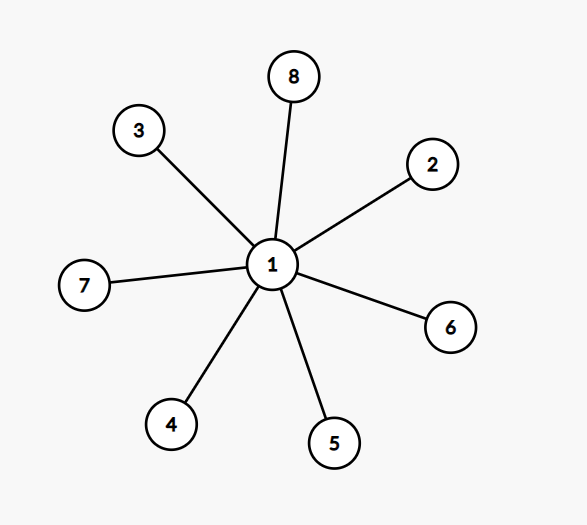
所以我们需要换一种思路：

对于每一个\(i\)，都计算出以\(i\)为中转点的联合权值的最大值和总和

具体实现：

我们把和\(i\)有连边的点的权值都放到一个数组\(w\)里面，排个序

• 最大值：即为\(w\)里面最大和次大的数的乘积
• 和：

和可以写成如下形式：（暂时不考虑\(w_i \times w_i\)的情况，在代码里面直接去掉就行了）

\(\sum_{i=1}^{n}\sum_{j=1}^{n}\ w_i \times w_j\)

令\(sum=\sum_{i=1}^{n}\)

根据乘法分配律，变成：\(\sum_{i=1}^{n}sum \times w_i\)

然后就可以直接把这个东西加到总和里面去了（注意不要忘了\(w_i \times w_i\)的情况）

code:

// Problem: P1351 [NOIP2014 提高组] 联合权值
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1351
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

/*houpingze \CCF/ \CCF/ \CCF/ \CCF/ \CCF/ */
/*
Note:

*/
#include<bits/stdc++.h>
#define reg register int
#define INF (1<<30)
#define pb push_back
#define vc vector
#define fst first
#define scd second
#define int long long
#define rep(i,x,y) for(int i=x;i<=y;i++)
using namespace std;
int read(){
	int res=0,fs=1; char c=getchar();
	while(!(c>='0' && c<='9')){ if(c=='-')fs=-1; c=getchar(); }
	while(c>='0' && c<='9')res=res*10+c-'0',c=getchar();
	return res*fs;
}
void print(int x){
    if(x<0) { putchar('-'); x=-x;}
    if(x>9) print(x/10);
    putchar(x%10+'0');
}
int n,cnt,m,a[500010],ans,tmp,k;
typedef pair<int,int> P;
//struct PROBLEM_SOLVER{
//	   int n,m;
//}solver;

//signed main(){
vector<int>G[200005];
int w[200005];
int mx,sum;
int wtmp[200005];
const int mod=10007;
void calc(int x){  
	int sonsize=G[x].size(),sum=0;
	rep(i,0,G[x].size()-1){
		wtmp[i+1]=w[G[x][i]];
		sum=(sum+wtmp[i+1])%mod;
	}
	sort(wtmp+1,wtmp+sonsize+1);
	mx=max(mx,wtmp[sonsize]*wtmp[sonsize-1]);
	rep(i,1,sonsize) ans=(ans+(sum-wtmp[i]+mod)*wtmp[i])%mod;
}
signed main() { 
	cin>>n;
	rep(i,1,n-1) {
		int u,v; 
        u=read(),v=read();
		G[u].pb(v);
		G[v].pb(u);
	}
	rep(i,1,n) w[i]=read();
	rep(i,1,n){ 
		calc(i);
	}
	cout<<mx<<' '<<ans ;
    return 0;
}