正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。故名高斯模糊。
一维正态分布的函数定义:
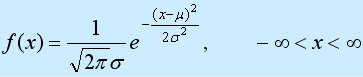
型随机变量的分布,第一参数μ是遵从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ2 )。 遵从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ,而取离μ越远的值的概率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。正态分布的密度函数的特点是:关于μ对称,在μ处达到最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点。它的形状是中间高两边低 ,图像是一条位于x轴上方的钟形曲线。当μ=0,σ2 =1时,称为标准正态分布,记为N(0,1)。
两个常数的意义:μ-期望,σ^2 方差。
下面我们解决第一个疑问:高斯模糊滤镜中的半径是什么?答案是高斯半径就是公式中的σ。
高斯曲线的图形和半径的含义如下图(来自Adobe SDK中技术支持专家的文档)所示:
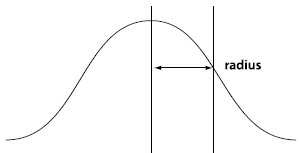
可见高斯半径(σ)对曲线形状的影响,σ越小,曲线越高越尖,σ越大,曲线越低越平缓。对二维图像来说,是一个钟形曲面,高斯半径越小,曲面越高越尖越陡峭;高斯半径越大,曲面越低越平缓。因此高斯半径越小,则模糊越小,高斯半径越大,则模糊程度越大。我们将看到ps对高斯半径的范围定义是【0.1~250】。当半径为0.1时,高斯模板在计算后只有中间像素为1,其他像素均=0(实际上只是趋近0),即图像不会有变化。
第二个疑问,高斯模板大小和高斯半径的关系?这是一个一直困扰我们的误解。因为我们的思维进入了物理实现的误区。在物理实现中,高斯模板有界,从而使我们忽略了这个问题的真正答案:高斯模板在逻辑上是无边界的。也就是说高斯模板本质上是逻辑上无穷拓展曲面的一个近似。因此,模板大小我们应该认为它是无穷大的。只不过在计算的时候,因为在远处趋近0,因此在某个阈值之下我们不再考虑这些值,这个阈值就是模板边界。
下面,二维高斯曲面的公式(x,y代表像素的模板坐标,模板中心位置为原点):
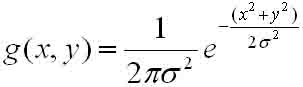
即:g(x,y)= ( 1 / (2*pi*σ^2) ) * exp( -(x^2+y^2)/(2*σ^2) ) ;
根据这个公式,我们可以计算出不同半径下的高斯模板,实际上模板是无穷大的,只是在中心较远处,他们会趋近0.例如,我们计算出r=0.7时的一个归一化后的高斯模板:
在网络上众所周知流传的高斯3*3模板实际上是对高斯曲面的一个整数除法形式的近似:
1 2 1
2 4 2 /16
1 2 1
实际验证,我们发现这个3*3模板实际上是对高斯半径约为0.849时的一个近似,当r=0.849时,其3*3归一模板为(在MATLAB中,输入h=fspecial('gaussian', 3, 0.849);即可得到这个模板):
(guass radius=0.849000)
0.062467 0.125000 0.062467
0.125000 0.250131 0.125000
0.062467 0.125000 0.062467
然后我们可以用Matlab中的imfilter来对图像进行高斯模糊的处理:
img = imread('c:\demo.bmp');
h = fspecial('gaussian', 3, 0.849);
img2 = imfilter(img, h);
subplot(121), imshow(img); title('原图')
subplot(122), imshow(img2); title('高斯模糊后')
效果如下:
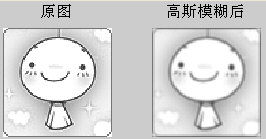
我们可以在Matlab中用如下语句绘制高斯曲面:
效果如下图:

在数字信号处理中,高斯模糊算法是一种滤波器,它的时域和频域曲线如下所示:
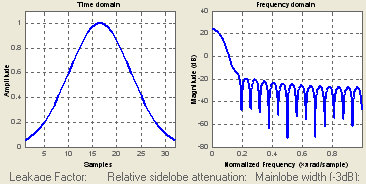
从频域曲线看出,高斯模糊本质上一种低通滤波器。体现在图像处理上,图像的边缘等灰度变化剧烈的地方对应高频信息,将被滤除。
最后,我们给出计算高斯模糊模板的C语言代码,请注意,由于高斯模板是对称的,实际上我们只需要计算出大约1/4模板即可。但这里的代码我们没有做这样的优化。我们输出的模板是(2*N+1)*(2N+1),高斯半径用r表示。
同时,作为比较,我们给出在Matlab中生成高斯模板的代码(fspecial的代码局部,其中p3是第三个参数即高斯半径):


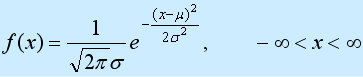 摘要: 最近有感于部分网友对高斯模糊滤镜的研究,本文将对高斯模糊中半径值的含义以及高斯模糊模板尺寸的疑惑做出总结和解答。
摘要: 最近有感于部分网友对高斯模糊滤镜的研究,本文将对高斯模糊中半径值的含义以及高斯模糊模板尺寸的疑惑做出总结和解答。

