Definition
Let
be a sequence of (complex) Hilbert spaces and
be the bounded operators from Hi to Hj.
A map A on  where
where
is called a positive definite kernel if for all m > 0 and
 , the following non-negativity condition holds:
, the following non-negativity condition holds:
bounded operator:http://www.encyclopediaofmath.org/index.php/Bounded_operator






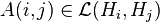


 浙公网安备 33010602011771号
浙公网安备 33010602011771号