最小二乘法

高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中。法国科学家勒让德于1806年独立发明“最小二乘法”，但因不为世人所知而默默无闻。勒让德曾与高斯为谁最早创立最小二乘法原理发生争执。

最小二乘法（Least Squares Method，又称最小平方法）是一种统计学和数学优化技术，旨在通过最小化误差的平方和，找到最能代表一组观测数据的函数（通常是曲线或直线）。 它是解决线性回归问题的经典算法。

1. 基本原理

该方法的核心思想是：当我们有一系列数据点(𝑥₁,𝑦₁),…,(𝑥_𝑛,𝑦_𝑛)，并假设一个数学模型𝑦=𝑓(𝑥;𝛽)（其中β（读音： beta）是模型的未知参数，比如直线的斜率和截距）可以描述这些数据时，最小二乘法试图找到最优的𝛽值，使得所有数据点的观察值 𝑦_𝑖 与模型预测值 𝑓(𝑥_𝑖; 𝛽) 之间的残差平方和（Sum of Squared Errors, SSE）达到最小。

残差平方和的数学表达式通常为：

 

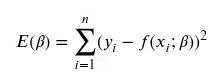通过使𝐸(𝛽)最小化，我们可以确定最佳拟合模型的参数。使用平方而不是其他形式（如绝对值）的好处在于，平方和函数通常是连续可微的，这使得应用微积分方法求解最优解变得简单且具有唯一性。 

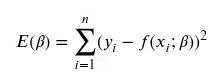
主要应用

2. 最小二乘法在多个领域都有广泛的应用：

• 线性回归：这是最常见的应用，用于确定最佳拟合直线，以描述两个变量之间的关系。
• 数据拟合：在科学实验中，用于将理论曲线拟合到实际测量的实验数据点上。
• 测量平差：在测绘学和地球物理学中，用于处理带有误差的观测数据，以获得最可靠的估计值。
• 机器学习：在线性回归等预测模型中作为核心优化算法。
• 经济学和工程学：用于时间序列分析、趋势预测和系统校准。
  

简而言之，最小二乘法提供了一种客观、数学严谨的方法来从有误差的数据中提取最有价值的信息和趋势。