带花树－一般图最大匹配

带花树

顾名思义，带花树是一种自带花朵的树（x）

　带花树其实并不是什么数据结构 ，它是一种以图为基础的 【匹配】 算法，常见于一般图匹配。

　生活中的匹配问题最常见是二分图匹配 ，一些匹配 也可以贪心 / DP 完成 ，但是遇到一般图，就很难跑出正确的匹配结果并输出了。

　介绍算法、讲解算法，我觉得各位巨巨【链接在底下】讲的已经十分清楚了，所以不再重复【主要是我觉得我讲的不比他们好】，但是网上好像还没人模拟带花树算法的过程，所以决定试一下模拟几个样例。

一：各个变量的含义：

二：算法核心：

　　匈牙利解决二分图偶环+奇环处理，其中使用的是匈牙利BFS版本解决二分图的情况

三：各个函数的介绍：

①主接口函数【返回一般图最大匹配】　很像二分图最大匹配的代码

　

 

②主函数BFS 用于搜索【增广路】 

 

 ③并查集代码+【pre指针和com指针共同作用下维护着一条原路径，可以理解为树的一条可以跳越的边】维护LCA代码　　

④缩环代码

 

 四：例子模拟

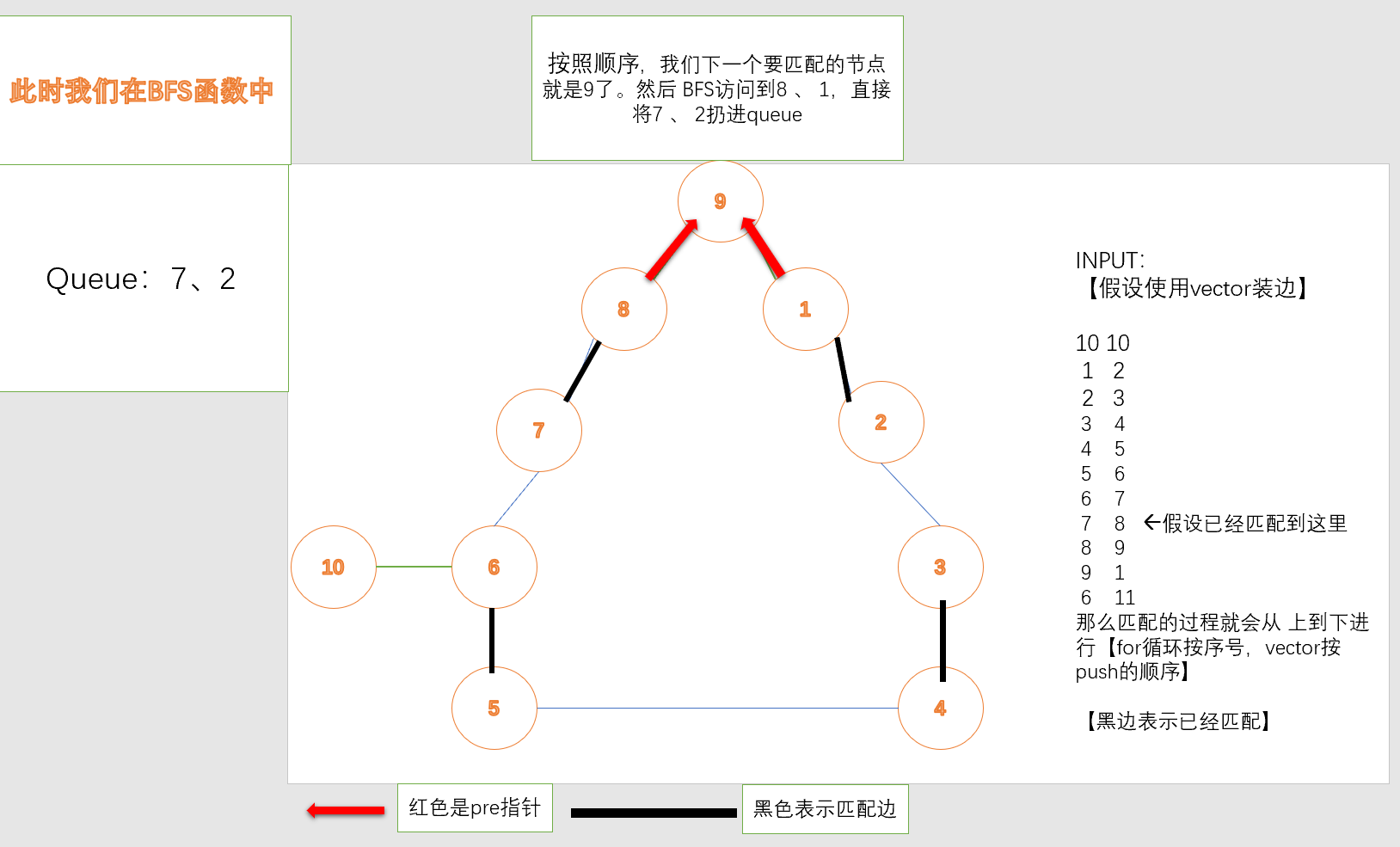
因为每次进入BFS函数都是未匹配的点，8已经被遍历到7时匹配了，所以直接跳过。 

 

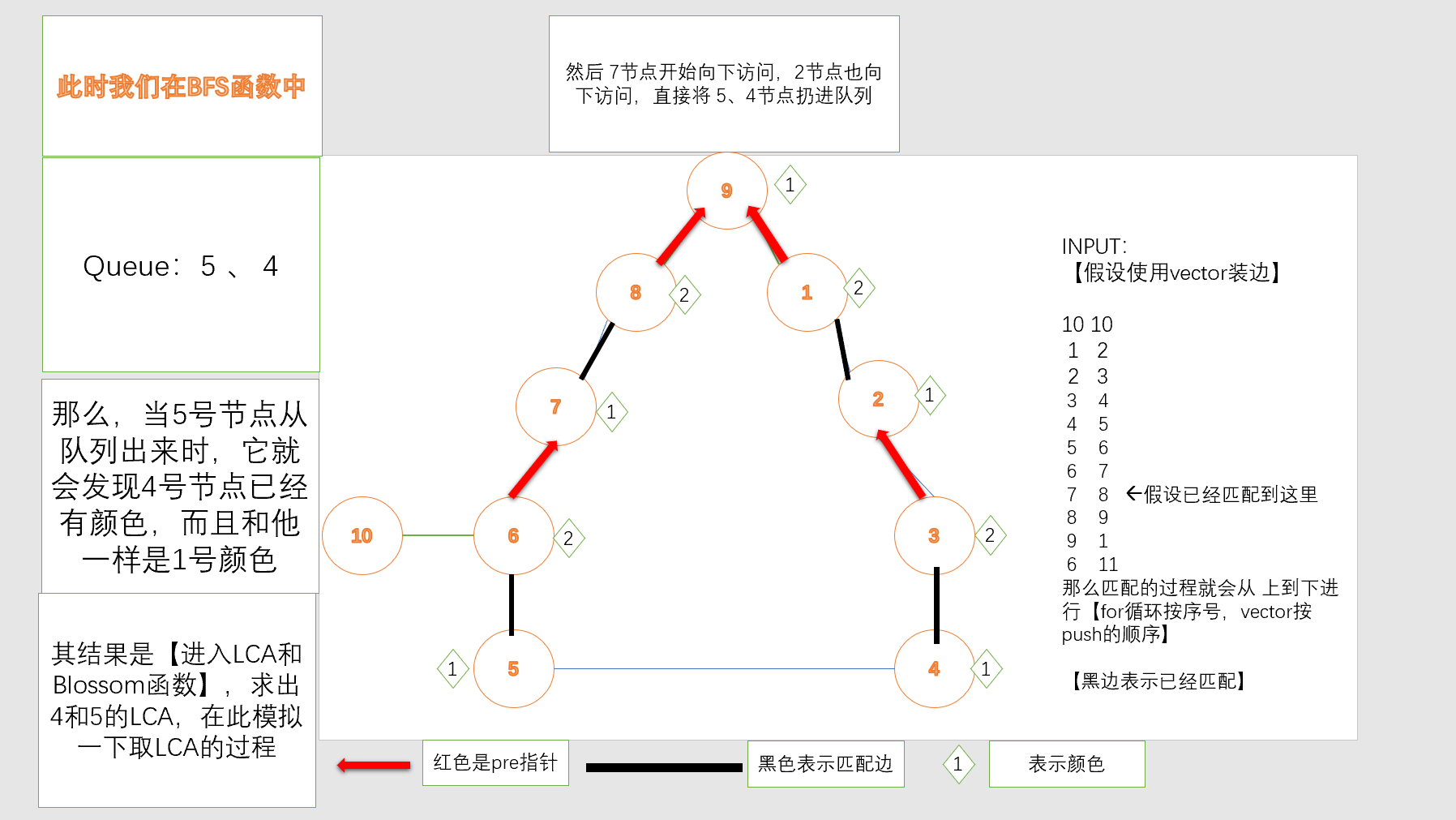
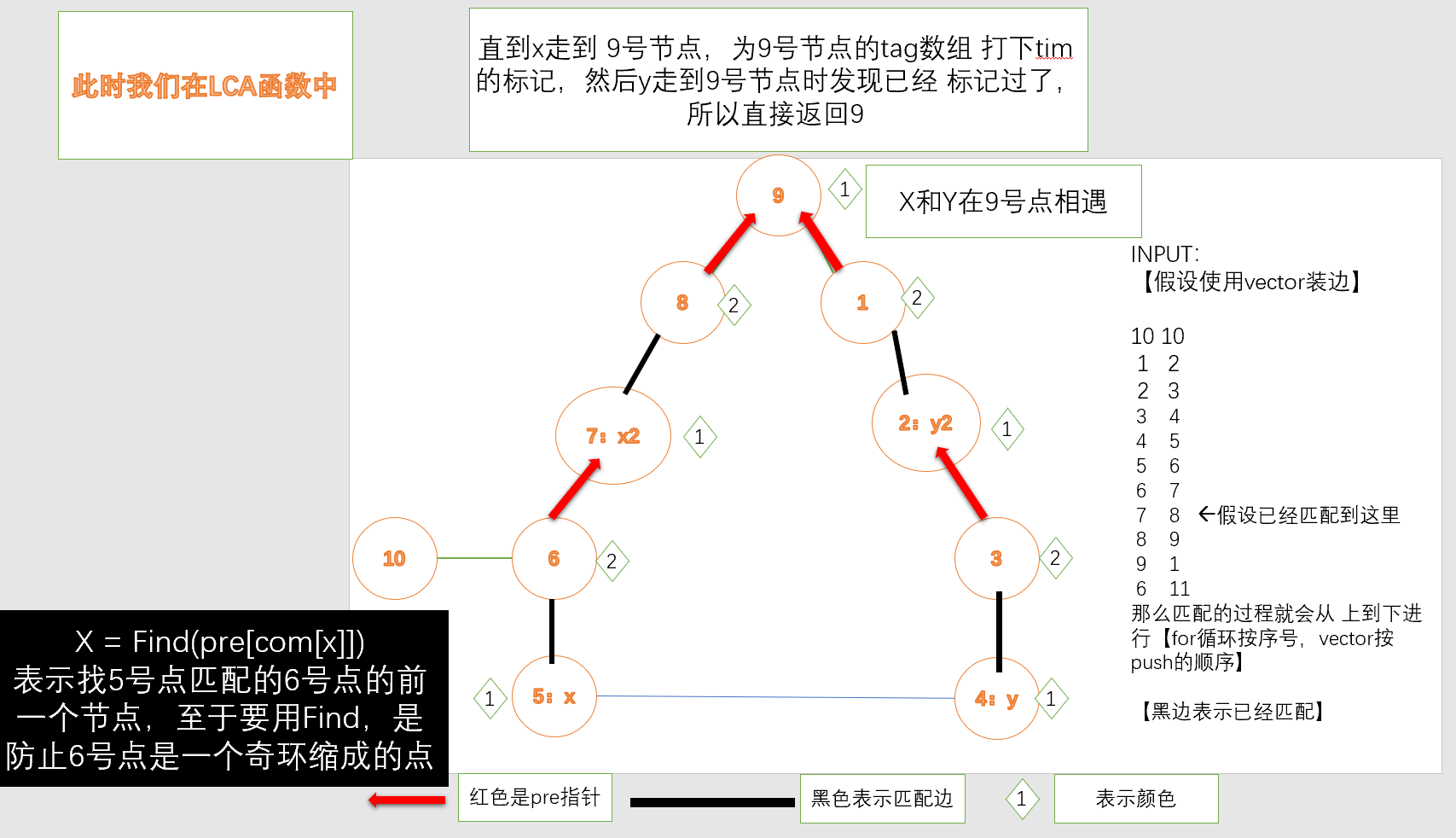
 【介绍完LCA函数，直接介绍重点：Blossom函数，为什么缩环的每一步都必不可少】

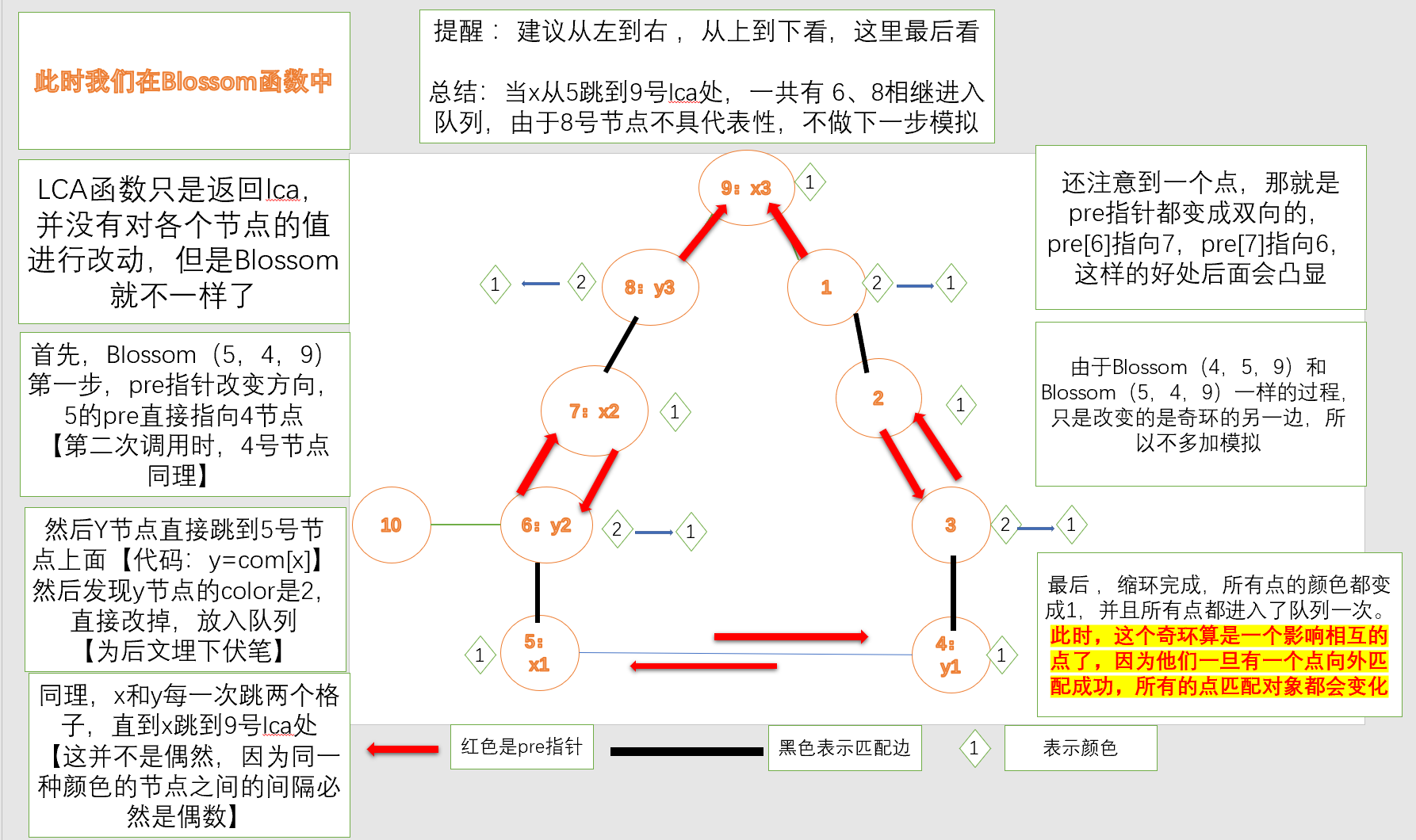
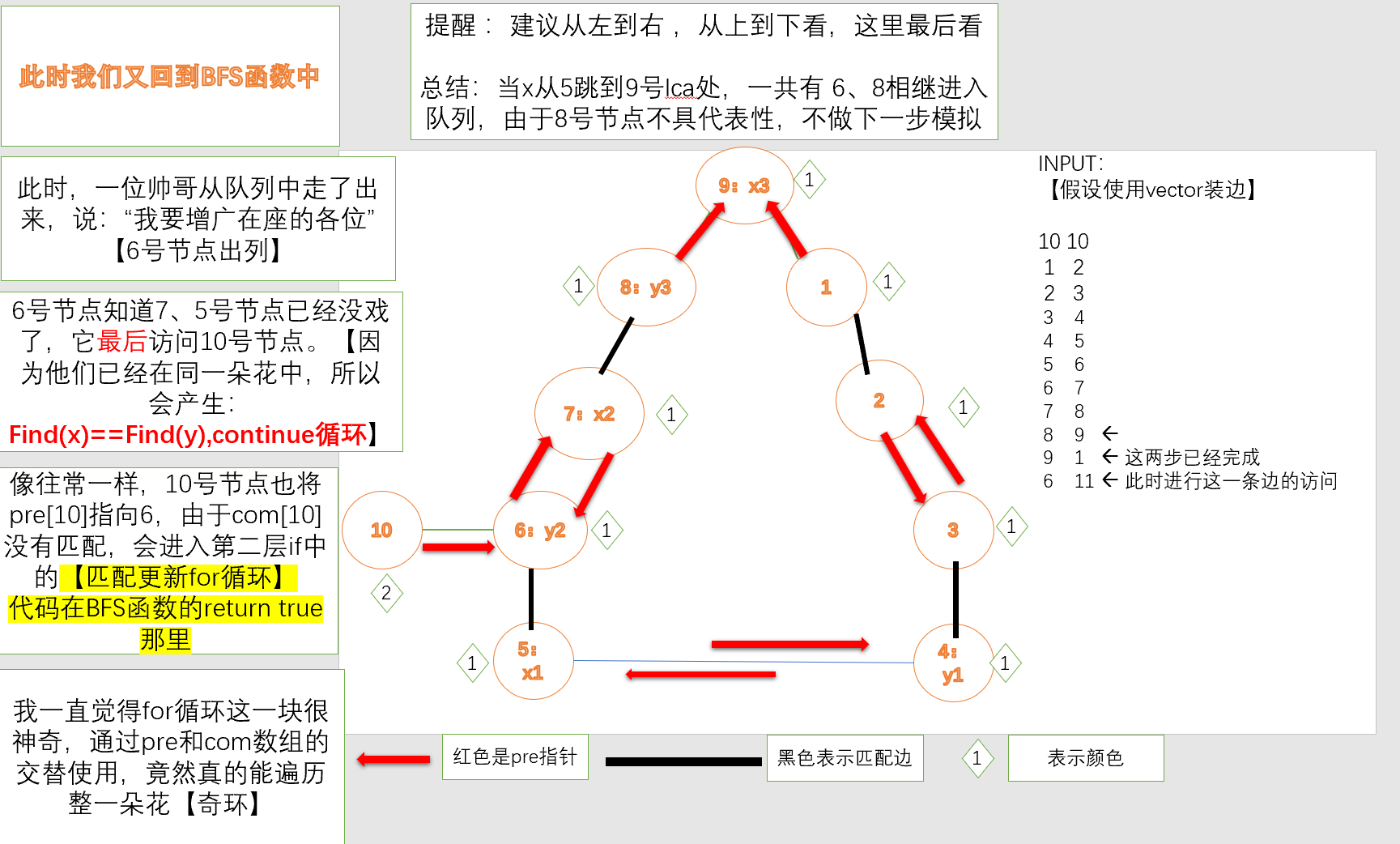
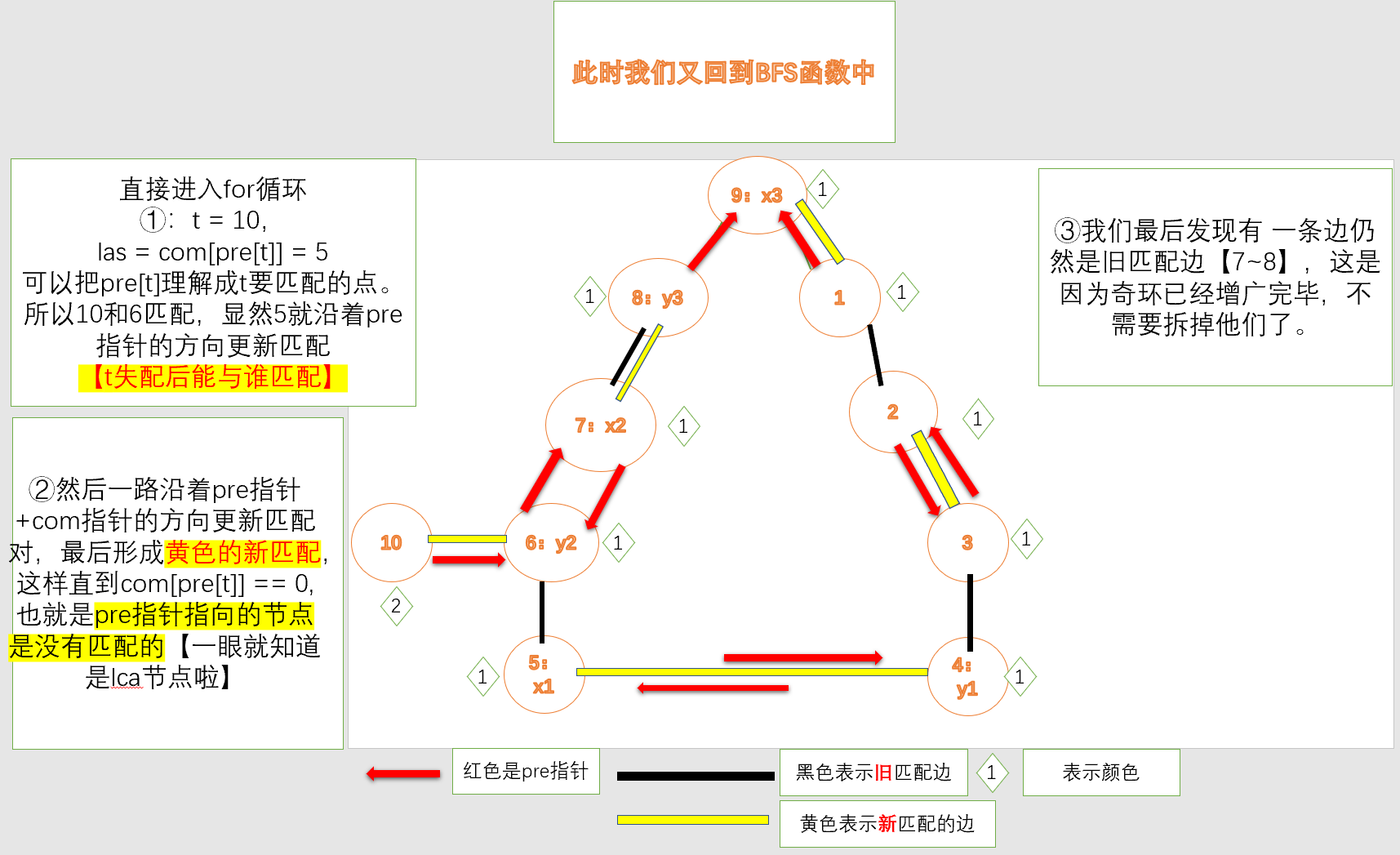
 五：笔者的补充

　模拟的样例虽然只有一个，但是用到了带花树算法的绝大部分代码，算是经典的样例，但是更复杂时会出现花套花的现象，不过处理方法与上面不禁相同，可以缩两次花解决掉。

　模拟的目的是帮助大家

　　①更好地理解pre数组和match数组（我代码是com数组），是如何形成双向链表的

　　②更好地理解for循环更新奇环匹配的过程。

　当然，理解了只是表层，如何更好地运用？如何解决特殊问题？都有待各位想出实际的做法。

 

namespace Match {
int com[maxn], col[maxn];
int tim, tag[maxn], N;
int fa[maxn], pre[maxn];
vector<vector<int>> e;

inline int Find(int x) { return x == fa[x] ? x : fa[x] = Find(fa[x]); }

inline int LCA(int x, int y) {
  ++tim;
  while (tag[x] != tim) {
    tag[x] = tim;
    x = Find(pre[com[x]]);
    if (y) swap(x, y);
  }
  return x;
}

queue<int> q;
inline void Blossom(int x, int y, int lca) {
  while (Find(x) != lca) {
    pre[x] = y, y = com[x];
    if (col[y] == 2) col[y] = 1, q.push(y);
    if (Find(x) == x) fa[x] = lca;
    if (Find(y) == y) fa[y] = lca;
    x = pre[y];
  }
}

inline int BFS(int S) {
  for (int i = 1; i <= N; i++) fa[i] = i, col[i] = pre[i] = 0;
  while (!q.empty()) q.pop();
  q.push(S), col[S] = 1;
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int &v : e[x]) {
      if (Find(v) == Find(x) || col[v] == 2) continue;
      if (!col[v]) {
        col[v] = 2, pre[v] = x;
        if (com[v] == 0) {
          for (int t = v, las; t != 0; t = las)
            las = com[pre[t]], com[t] = pre[t], com[pre[t]] = t;
          return 1;
        }
        col[com[v]] = 1, q.push(com[v]);
      } else {
        int lca = LCA(x, v);
        Blossom(x, v, lca);
        Blossom(v, x, lca);
      }
    }
  }
  return 0;
}

inline int maxMatch() {
  me(com, 0), me(tag, 0), tim = 0;
  int ans = 0;
  for (int i = 1; i <= N; i++)
    if (com[i] == 0 && BFS(i)) ans++;
  return ans;
}
// 初始化图，并且设置节点数量
inline void initMaxMatch(int n) { N = n, e.assign(n + 1, vector<int>()); }

};  // namespace Match
using namespace Match;

 

题库：

（1）Luogu：板子题

（2）UOJ79：传送门

（3）Kuangbin带你飞 ：传送门

HDU： 带花树--除去多余组合【多余组合：删掉这个组合之后，会使最大匹配的结果-2（因为本来这个组合的两个端点分别属于不同的匹配对，删掉之后两个匹配对都没了，所以-2。如果不是多余，即本来他们有机会组合在一起，所以删掉他们只会 使得最大匹配结果-1）】【例如下图，删去任意两个节点的所有边（甚至删去节点），剩下图的匹配对都只是-1】

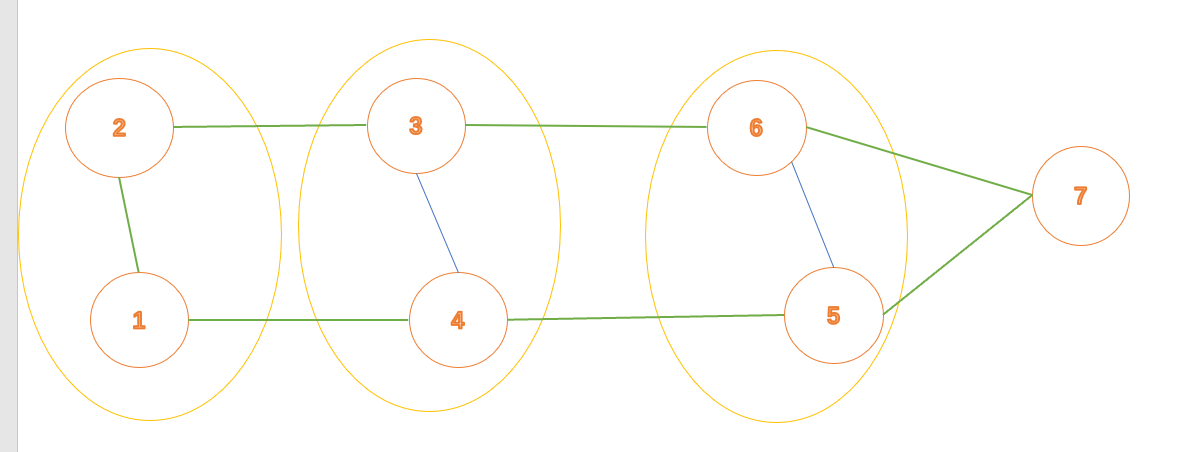
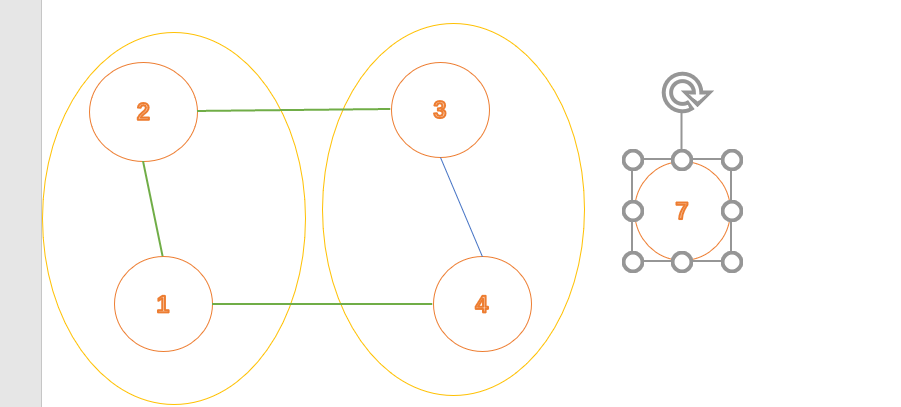
比如 样例1：  1 - 3 - 2 - 4 ，去掉2-3，最大匹配-2.

【如果选了2-3作为匹配，那么匹配的数量就是1了，但是正确的最大匹配是2 】

 注意一下输出的格式，就算0也要加多一个换行

//#pragma GCC optimize(3, "inline", "-Ofast")
#include <bits/stdc++.h>

#include <ext/pb_ds/priority_queue.hpp>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  T x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e3 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-8;

int n, m, k, t1, t2, t3;

namespace Match {
int com[maxn], col[maxn];
int tim, tag[maxn], N, banU, banV;
int fa[maxn], pre[maxn];
vector<vector<int>> e;

inline int Find(int x) { return x == fa[x] ? x : fa[x] = Find(fa[x]); }

inline int LCA(int x, int y) {
  ++tim;
  while (tag[x] != tim) {
    tag[x] = tim;
    x = Find(pre[com[x]]);
    if (y) swap(x, y);
  }
  return x;
}

queue<int> q;
inline void Blossom(int x, int y, int lca) {
  while (Find(x) != lca) {
    pre[x] = y, y = com[x];
    if (col[y] == 2) col[y] = 1, q.push(y);
    if (Find(x) == x) fa[x] = lca;
    if (Find(y) == y) fa[y] = lca;
    x = pre[y];
  }
}

inline int BFS(int S) {
  for (int i = 1; i <= N; i++) fa[i] = i, col[i] = pre[i] = 0;
  while (!q.empty()) q.pop();
  q.push(S), col[S] = 1;
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    if (x == banU || x == banV) continue;  // 特判这个点是不是被删除
    for (int &v : e[x]) {
      if (v == banV || v == banU) continue;  // 特判这条边是不是不能使用
      if (Find(v) == Find(x) || col[v] == 2) continue;
      if (!col[v]) {
        col[v] = 2, pre[v] = x;
        if (com[v] == 0) {
          for (int t = v, las; t != 0; t = las)
            las = com[pre[t]], com[t] = pre[t], com[pre[t]] = t;
          return 1;
        }
        col[com[v]] = 1, q.push(com[v]);
      } else {
        int lca = LCA(x, v);
        Blossom(x, v, lca);
        Blossom(v, x, lca);
      }
    }
  }
  return 0;
}

inline int maxMatch() {
  me(com, 0), me(tag, 0), tim = 0;
  int ans = 0;
  for (int i = 1; i <= N; i++)
    if (com[i] == 0 && BFS(i)) ans++;
  return ans;
}
// 初始化图，并且设置节点数量
inline void initMaxMatch(int n) { N = n, e.assign(n + 1, vector<int>()); }

};  // namespace Match
using namespace Match;

void solve() {
  vector<PII> pe;
  initMaxMatch(n);
  for (int i = 1, x, y; i <= m; i++) {
    read(x, y);
    e[x].emp(y), e[y].emp(x);
    pe.emp(mp(x, y));
  }
  banU = banV = 0;
  int mx = maxMatch();
  vector<int> ans;
  for (int i = 1; i <= m; i++) {
    banU = pe[i - 1].fi, banV = pe[i - 1].se;
    if (maxMatch() == mx - 2) ans.emp(i);
  }
  printf("%d\n", ans.size());
  for (int i = 0; i < ans.size(); i++) {
    if (i) printf(" ");
    printf("%d", ans[i]);
  }
  pln;
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  // read(TEST);
  while (~scanf("%d%d", &n, &m)) solve();
}

/*
 */

 

（4）ZOJ3316：Game

跑带花树，最后再跑n次com[I]，check一下。【不知道为什么Match()==n/2 会错 】

#include <stdio.h>
#include <iostream>
#include <ctime>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <stack>
#pragma GCC optimize(3)
#define lowbit(x) (x&~x)//~为按位取反再加1
#define re register
#define ls (ro<<1)
#define rs ((ro<<1)|1)
#define ll long long
#define ull unsigned long long
#define fi first
#define se second
#define de(a) cerr<<#a<<" = "<<a<<endl
#define emp(a)  emplace_back(a)
#define iter(c)   __typeof((c).begin())
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
inline ll max(ll a,ll b){return a>b?a:b;}
inline ll min(ll a,ll b){return a>b?b:a;}
template<typename T>inline int read(T&res){
    ll x=0,f=1,flag=0;char ch;
    flag=ch=getchar();
    if(flag==-1)return -1;
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        flag=ch=getchar();
        if(flag==-1)return -1;
    }
    while(ch>='0'&&ch<='9'&&flag!=-1){
        x=(x<<1)+(x<<3)+(ch^48);
        flag=ch=getchar();
    }
    res = x*f;return flag;
}
template<typename T,typename...Args>
inline int read(T&t,Args&...a){
    int res;
    res=read(t);if(res==-1)return -1;
    res=read(a...);return res;
}
const int maxn = 555,inf = 0x3f3f3f3f;
int com[maxn],col[maxn];
int tim,tag[maxn];
int fa[maxn],pre[maxn];
int n,m,a,b,c,L;
vector<int>e[maxn];
struct stone
{
    int x,y,id;
}s[maxn];

inline int Find(int x){return x==fa[x]?x:fa[x]=Find(fa[x]);}

inline int LCA(int x,int y)
{
    ++tim;
    while(tag[x]!=tim)
    {
        tag[x] = tim;
        x = Find(pre[com[x]]);
        if(y)swap(x,y);
    }
    return x;
}

queue<int>q;
inline void Blossom(int x,int y,int lca)
{
    while(Find(x)!=lca)
    {
        pre[x] = y , y = com[x];
        if(col[y] == 2)
            col[y] = 1,q.push(y);
        if(Find(x)==x)fa[x] = lca;
        if(Find(y)==y)fa[y] = lca;
        x = pre[y];
    }
}

inline int BFS(int S)
{
    for(int i = 1;i <= n;i++)
        fa[i]=i,col[i]=pre[i]=0;
    while(!q.empty())q.pop();
    q.push(S),col[S]=1;

    while(!q.empty())
    {
        int x = q.front();q.pop();
        for(int v:e[x])
        {
            if(Find(v) == Find(x) || col[v] == 2)continue;
            if(!col[v])
            {
                col[v] = 2; pre[v] = x;
                if(com[v] == 0)
                {
                    for(int t=v,las;t != 0;t=las)
                        las = com[pre[t]],
                        com[t] = pre[t],
                        com[pre[t]] = t;
                    return 1;
                }
                col[com[v]] = 1,q.push(com[v]);
            }
            else
            {
                int lca = LCA(x,v);
                Blossom(x,v,lca);
                Blossom(v,x,lca);
            }
        }
    }
    return 0;
}

int Match()
{
    me(com,0),me(tag,0),tim = 0;
    int ans = 0;
    for(int i = 1;i <= n;i++)
    if(com[i] ==0 && BFS(i))
        ans++;
    return ans;
}
bool check()
{
    for(int i = 1;i <= n;i++)
        if(com[i]==0)return 0;
    return 1;
}

void solve()
{
    for(int i = 0;i <= n;i++)e[i].clear();
    for(int i = 1;i <= n;i++)
    {
        scanf("%d%d",&s[i].x,&s[i].y);
        s[i].id =  i;
    }
    read(L);
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1+i;j <= n;j++)
        {
            if(abs(s[i].x-s[j].x)+abs(s[i].y-s[j].y)<=L)
            e[i].emp(j),e[j].emp(i);
        }
    }
    int ans = Match();
    //de(ans);
    if(check())puts("YES");
    else puts("NO");
}


int main()
{
//这些ifdef要在main函数里面

#ifndef ONLINE_JUDGE
    //freopen("rand.in","r",stdin);
    //freopen("baoli.out","w",stdout);
    ll sta = clock();
#endif

    int t = 1,kase = 1;
    //~scanf("%d",&t);
    //while(t--)
    while(~read(n))
        solve();



#ifndef ONLINE_JUDGE
    ll en = clock();
    cerr<<"运行时间"<<(double)(en-sta)<<"ms"<<endl;
#endif
}

 

（5）UOJ171：挑战NPC 【拆点建图】

关于这道题的理解：由于一个框拆成了3个框，所以对答案起作用的部分只有：两个框之间的匹配。

①如果该框有0个球，那么匹配数为1，属于两个框之间的匹配，答案+1

②如有一个球，那么匹配数为2，其中只有一个属于了两个框的匹配，答案+1

③对于2，3个球的情况，匹配数为球的数量，两个框不可能存在匹配，所以答案为0。

综上，每个框对最大匹配的贡献 = 该框内球的数量 + 两个分框的匹配数

又由于题目强制所有球都要放进去，所以半框的答案就是： maxMatch - n

#include <stdio.h>
#include <iostream>
#include <ctime>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <stack>
#pragma GCC optimize(3)
#define lowbit(x) (x&~x)//~为按位取反再加1
#define re register
#define ls (ro<<1)
#define rs ((ro<<1)|1)
#define ll long long
#define ull unsigned long long
#define fi first
#define se second
#define de(a) cerr<<#a<<" = "<<a<<endl
#define emp(a)  emplace_back(a)
#define iter(c)   __typeof((c).begin())
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
inline ll max(ll a,ll b){return a>b?a:b;}
inline ll min(ll a,ll b){return a>b?b:a;}
template<typename T>inline int read(T&res){
    ll x=0,f=1,flag=0;char ch;
    flag=ch=getchar();
    if(flag==-1)return -1;
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        flag=ch=getchar();
        if(flag==-1)return -1;
    }
    while(ch>='0'&&ch<='9'&&flag!=-1){
        x=(x<<1)+(x<<3)+(ch^48);
        flag=ch=getchar();
    }
    res = x*f;return flag;
}
template<typename T,typename...Args>
inline int read(T&t,Args&...a){
    int res;
    res=read(t);if(res==-1)return -1;
    res=read(a...);return res;
}
const int maxn = 3555,inf = 0x3f3f3f3f;
int com[maxn],col[maxn];
int tim,tag[maxn];
int fa[maxn],pre[maxn];
int n,m,k,t1,t2,t3,a,b,c,L;
vector<int>e[maxn];

inline int Find(int x){return x==fa[x]?x:fa[x]=Find(fa[x]);}

inline int LCA(int x,int y)
{
    ++tim;
    while(tag[x]!=tim)
    {
        tag[x] = tim;
        x = Find(pre[com[x]]);
        if(y)swap(x,y);
    }
    return x;
}

queue<int>q;
inline void Blossom(int x,int y,int lca)
{
    while(Find(x)!=lca)
    {
        pre[x] = y , y = com[x];
        if(col[y] == 2)
            col[y] = 1,q.push(y);
        if(Find(x)==x)fa[x] = lca;
        if(Find(y)==y)fa[y] = lca;
        x = pre[y];
    }
}

inline int BFS(int S)
{
    for(int i = 1;i <= t3;i++)
        fa[i]=i,col[i]=pre[i]=0;
    while(!q.empty())q.pop();
    q.push(S),col[S]=1;

    while(!q.empty())
    {
        int x = q.front();q.pop();
        for(int v:e[x])
        {
            if(Find(v) == Find(x) || col[v] == 2)continue;
            if(!col[v])
            {
                col[v] = 2; pre[v] = x;
                if(com[v] == 0)
                {
                    for(int t=v,las;t != 0;t=las)
                        las = com[pre[t]],
                        com[t] = pre[t],
                        com[pre[t]] = t;
                    return 1;
                }
                col[com[v]] = 1,q.push(com[v]);
            }
            else
            {
                int lca = LCA(x,v);
                Blossom(x,v,lca);
                Blossom(v,x,lca);
            }
        }
    }
    return 0;
}

int Match()
{
    me(com,0),me(tag,0),tim = 0;
    int ans = 0;
    for(int i = 1;i <= t3;i++)
    if(com[i] ==0 && BFS(i))
        ans++;
    return ans;
}

void solve()
{
    read(n,m,k);
    t1 = n+m,t2 = t1+m,t3 = t2+m;
    for(int i = 0;i <= t3;i++)e[i].clear();
    for(int i = 1;i <= m;i++)
    {
        e[i+n].emp(i+t2),e[i+n].emp(i+t1);
        e[i+t1].emp(i+n),e[i+t1].emp(i+t2);
        e[i+t2].emp(i+n),e[i+t2].emp(i+t1);
    }
    for(int i = 1;i <= k;i++)
    {
        read(a,b);
        e[a].emp(b+n),e[a].emp(b+t2),e[a].emp(b+t1);
        e[b+n].emp(a),e[b+t2].emp(a),e[b+t1].emp(a);
    }
    int ans = Match();
    printf("%d\n",ans-n);
    for(int i = 1;i <= n;i++)
        com[i]-=n,printf("%d ",(com[i]%m==0?m:com[i]%m));
    puts("");
}



int main()
{
//这些ifdef要在main函数里面

#ifndef ONLINE_JUDGE
    //freopen("rand.in","r",stdin);
    //freopen("baoli.out","w",stdout);
    ll sta = clock();
#endif

    int t = 1,kase = 1;
    ~scanf("%d",&t);
    while(t--)
    //while(~read(n))
        solve();



#ifndef ONLINE_JUDGE
    ll en = clock();
    cerr<<"运行时间"<<(double)(en-sta)<<"ms"<<endl;
#endif
}

题解转载这里

你可以列一个表格。

一个框子里放球的数量	0	1	2	3
对“半空框子”数量的贡献	1	1	0	0

把一个框子拆三个点。两两之间连边。
会发现，如果这三个点里一个都没有被球匹配掉，那么这三个点的最大匹配数是11；如果任意一个点被一个球匹配掉了，那么剩下两个点一定可以匹配，所以最大匹配数还是11；有两个点或者是三个点被匹配后最大匹配就是00。
所以，按如上方式建图，每个球向它可以放进的框子对应的的三个点都连边。跑出最大匹配后输出ans−nans−n就好了。（因为nn个球是一定可以被匹配的）

update：yyb跟我说他在WA了若干次后发现了一件有趣的事情。
因为只有增广成功时才会修改匹配，所以如果先匹配框子再匹配球的话，不能保证球一定出现在最大匹配中，所以在输出方案的时候会出问题。
所以就一定要先匹配球再匹配框子。【即match函数里面的for循环要从1~t3，而不是t3~1】

 

（6）清楚姐姐的翅膀们 【牛客： 拆点建图】

考虑拆点，由于每个妹子只需要两个就可以开心，所以只需要拆成两个点，那么这两个点之间自带一条边。

然后分析：

①如果一个妹子获得0个蝴蝶结，那么她与蝴蝶结的匹配数为0，与自身的匹配数为1，总匹配为1

②如果一个妹子获得1个蝴蝶结，那么她与蝴蝶结匹配数为1，与自身匹配为0，总匹配为1

③如果获得2个，以此类推，总匹配为2

那么显然，只需要将每个妹子的总匹配数 - 1 = 开心的妹子的数量

所以总得加起来就是： maxMatch -　妹子数量

//#pragma GCC optimize(3, "inline", "-Ofast")
#include <bits/stdc++.h>

#include <ext/pb_ds/priority_queue.hpp>
#define lowbit(x) (x & (-x))  //-为按位取反再加1
#define mseg ((l + r) >> 1)
#define ls (ro << 1)
#define rs ((ro << 1) | 1)
#define ll long long
#define lld long double
#define uint unsigned int
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define ios_fast ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define deline cout << "-----------------------------------------" << endl
#define de(a) cout << #a << " = " << a << endl
#define de2(a, b) de(a), de(b), deline
#define de3(a, b, c) de(a), de(b), de(c), deline
#define de4(a, b, c, d) de(a), de(b), de(c), de(d), deline
#define emp(a) push_back(a)
#define iter(c) __typeof((c).begin())
#define PII pair<int, int>
#define PLL pair<ll, ll>
#define me(x, y) memset((x), (y), sizeof(x))
#define mp make_pair
using namespace std;
/////快读
template <typename T>
inline void read(T &res) {  //
  T x = 0, f = 1;
  char ch = getchar();
  while (ch != EOF && (ch < '0' || ch > '9')) {
    if (ch == '-') f = -1;
    ch = getchar();
  }
  while (ch != EOF && ch >= '0' && ch <= '9') {
    x = (x << 1) + (x << 3) + (ch ^ 48);
    ch = getchar();
  }
  res = x * f;
}
template <typename T, typename... Args>
inline void read(T &t, Args &...a) {
  read(t), read(a...);
}

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e3 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-8;

int n, m, k, t1, t2, t3;

namespace Match {
int com[maxn], col[maxn];
int tim, tag[maxn], N;
int fa[maxn], pre[maxn];
vector<vector<int>> e;

inline int Find(int x) { return x == fa[x] ? x : fa[x] = Find(fa[x]); }

inline int LCA(int x, int y) {
  ++tim;
  while (tag[x] != tim) {
    tag[x] = tim;
    x = Find(pre[com[x]]);
    if (y) swap(x, y);
  }
  return x;
}

queue<int> q;
inline void Blossom(int x, int y, int lca) {
  while (Find(x) != lca) {
    pre[x] = y, y = com[x];
    if (col[y] == 2) col[y] = 1, q.push(y);
    if (Find(x) == x) fa[x] = lca;
    if (Find(y) == y) fa[y] = lca;
    x = pre[y];
  }
}

inline int BFS(int S) {
  for (int i = 1; i <= N; i++) fa[i] = i, col[i] = pre[i] = 0;
  while (!q.empty()) q.pop();
  q.push(S), col[S] = 1;
  while (!q.empty()) {
    int x = q.front();
    q.pop();
    for (int &v : e[x]) {
      if (Find(v) == Find(x) || col[v] == 2) continue;
      if (!col[v]) {
        col[v] = 2, pre[v] = x;
        if (com[v] == 0) {
          for (int t = v, las; t != 0; t = las)
            las = com[pre[t]], com[t] = pre[t], com[pre[t]] = t;
          return 1;
        }
        col[com[v]] = 1, q.push(com[v]);
      } else {
        int lca = LCA(x, v);
        Blossom(x, v, lca);
        Blossom(v, x, lca);
      }
    }
  }
  return 0;
}

inline int maxMatch() {
  me(com, 0), me(tag, 0), tim = 0;
  int ans = 0;
  for (int i = 1; i <= N; i++)
    if (com[i] == 0 && BFS(i)) ans++;
  return ans;
}
// 初始化图，并且设置节点数量
inline void initMaxMatch(int n) { N = n, e.assign(n + 1, vector<int>()); }

};  // namespace Match
using namespace Match;

void solve() {
  read(m, n);
  t1 = n + m, t2 = t1 + m;
  initMaxMatch(t2);
  for (int b = 1, a, c; b <= m; b++) {
    read(c);
    while (c--) {
      read(a);
      e[a].emp(b + n), e[a].emp(b + t1);
      e[b + n].emp(a), e[b + t1].emp(a);
    }
    e[n + b].emp(b + t1), e[t1 + b].emp(n + b);
  }
  int ans = maxMatch();
  printf("%d\n", ans - m);
}

int main() {
  // freopen("test_input.txt", "r", stdin);
  // freopen("test_output.txt", "w", stdout);
  int TEST = 1;
  read(TEST);
  while (TEST--) solve();
}

/*
 */

 

 

最后，感谢也推荐大佬们的Blog：

　【1】带花树算法精讲

　【2】带花树

　【3】带花树讲解

　【4】带花树2

　【5】带花树3

 

 

后记：

①网上冲浪发现了一些特别的方法来解决一般图的最大匹配问题，其中最特别的是：随机化+匈牙利DFS

但是好像遇到特别的数据会被卡【但我也不知道是什么特别的数据】

②另外，带花树多重匹配、最权匹配可能之后会继续写下去

③如果图论学得差不多会考虑一下看看论文什么的，继续加固一下知识。。