深度学习-激活函数
- 激活函数
作用:增强网络的非线性能力
扩展:1:神经网络为什么要引入非线性?
如果神经网路没有引入非线性层,那么神经网络就变成了线性层的堆叠,堆叠后的表达式还是一个线性函数,线性函数的表达能力是有限的,它只能表示特征和目标值之间比较简单的关系,引入非线性层可以提高网络的表达能力,和鲁棒性
激活函数介绍:
sigmoid函数
公式:
![]()
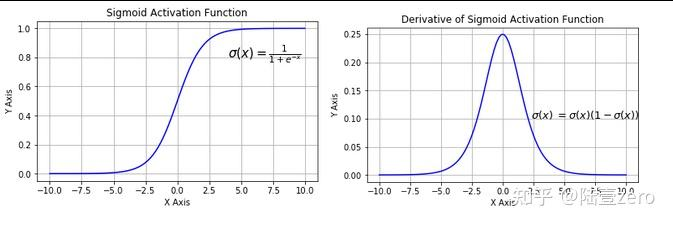
函数图像:
优点:![]()
1:输出范围(0,1)可以用于二分类
2:连续函数方便求导
缺点:
1:在极大值和极小值时会出现梯度消失,梯度消失会导致在深度神经网络中反向传播时无法更新参数
2:函数的输出值不是以0为均值,如果函数值全部大于0或小于0会导致反向传播更新参数时所有参数的更新方向一致,可能导致收敛速度变慢
3:运算复杂度高,函数为指数函数![]()
Tanh函数(双曲正切函数)
函数:
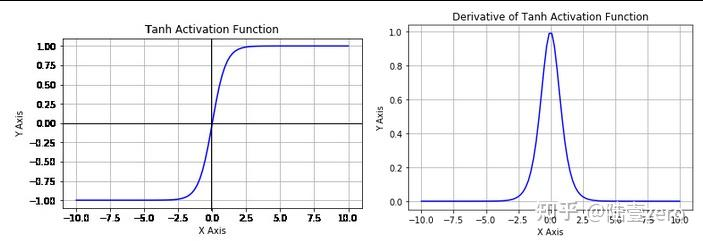
函数图像:![]()
优点:![]()
1:输出值以0为中心,加快收敛速度
2:连续函数方便求导
缺点:
1:存在梯度消失问题
2:运算复杂度高,存在指数函数
ReLU函数(Rectified linear unit 线性修正单元)
函数:
![]()
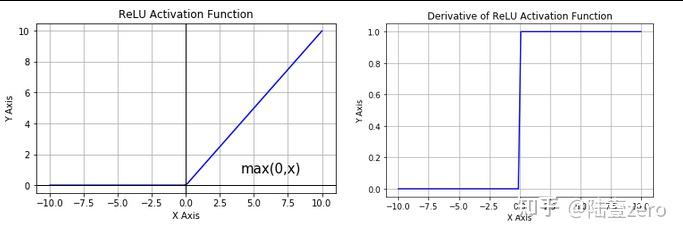
函数图像
优点:![]()
1:计算简单,只需要进行一次比较运算和一次取最大值的运算,收敛速度快
2:避免梯度消失,x>0范围下不会出现梯度消失
3:有助于稀疏化, ReLU函数对于负数输入的输出均为0,这种截断效果可以使得网络中一部分神经元对于某些输入永远不会被激活,从而实现神经元的稀疏化。稀疏化可以减少参数的数量,进而降低过拟合的风险,并提高网络的泛化能力。
缺点:
1:输出值不是以0为均值
2:神经元坏死,在x<0时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。
Leaky ReLU函数
PReLUhanshu
RReLU函数
ELU函数
SELU函数
Maxout函数
Softmac函数
Swish函数
Softplus函数 - 损失函数
- 优化器


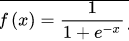

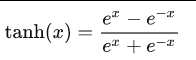
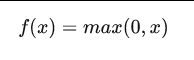

 浙公网安备 33010602011771号
浙公网安备 33010602011771号