平面几何

向量：拥有大小和方向的量

性质

向量没有位置属性
向量的大小被称为向量的模，记作\(|AB|\)
可以用A点到B点的有向线段\(\overrightarrow{AB}\)表示向量

反向量

大小相同且方向相反的向量

向量加减法

对每个维度分别相加/相减，向量减法也相当于被减向量加上减向量的反向量。

向量点乘和向量叉乘

向量点乘

点乘符号为 \(•\)，\(\overrightarrow{OP}•\overrightarrow{OQ}=|\overrightarrow{OP}|\ | \overrightarrow{OQ}|\ cos\ \theta\)，其中\(\theta\)为\(\overrightarrow{OP}\)和\(\overrightarrow{OQ}\)的夹角。即\(\overrightarrow{OQ}\)到\(\overrightarrow{OP}\)的投影长度与\(\overrightarrow{OP}\)的长度相乘。
点乘的结果被称为点积，又被称为内积，是标量。令\(\overrightarrow{OP} = (x1, y1)， \overrightarrow{OQ} = (x2, y2)\)，则\(\overrightarrow{OP} • \overrightarrow{OQ} = x1 * x2 + y1 * y2\)。
向量点乘满足交换律

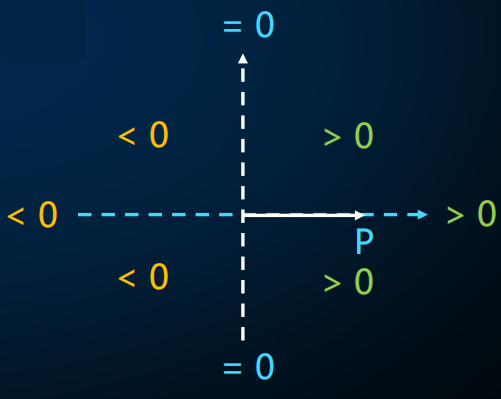
点乘可以判断向量的前后关系

根据参照向量\(\overrightarrow{OP}\)建立直角坐标系，\(O\)为原点，\(\overrightarrow{OP}\)方向为x正轴。

• 当Q在一、四象限或x正轴上时，有\(\overrightarrow{OP}•\overrightarrow{OQ}>0\)。
• 当Q在二、三象限或x负轴上时，有\(\overrightarrow{OP}•\overrightarrow{OQ}<0\)。
• 当Q在y轴上时，有\(\overrightarrow{OP}•\overrightarrow{OQ}=0\)。
  

向量叉乘

叉乘符号为 \(\times\)， \(|\overrightarrow{OP} × \overrightarrow{OQ}| = |\overrightarrow{OP}|\ | \overrightarrow{OQ} |\ sin\ \theta\)，其中\(\theta\)为\(\overrightarrow{OP}\)和\(\overrightarrow{OQ}\)的夹角。即Q到OP的距离与\(\overrightarrow{OP}\)的长度相乘。
叉乘的结果被称为叉积，又被称为外积，是向量。令\(\overrightarrow{OP} = (x1, y1)， \overrightarrow{OQ} = (x2, y2)\)，则\(|\overrightarrow{OP} × \overrightarrow{OQ}| = x1 * y2 - y1 * x2\)。

叉乘满足交换律吗？

• 不满足，\(\overrightarrow{OP} × \overrightarrow{OQ} = -(\overrightarrow{OQ} × \overrightarrow{OP}) = \overrightarrow{OQ} × -\overrightarrow{OP}\)。
• 交换位置或者取反某个向量都会导致叉乘结果反向。

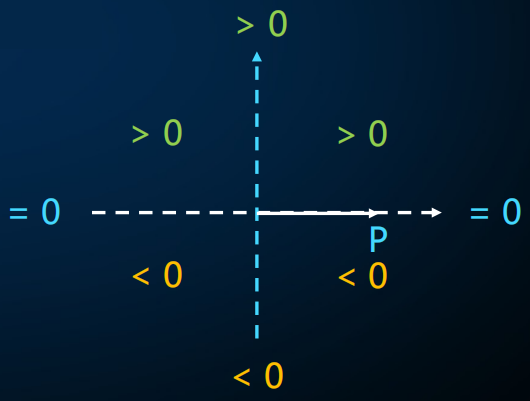
叉乘可以判断向量的左右关系

根据参照向量\(\overrightarrow{OP}\)建立直角坐标系，\(O\)为原点，\(\overrightarrow{OP}\)方向为x正轴。

• 当Q在一、二象限或y正轴上时，有\(\overrightarrow{OP}\times\overrightarrow{OQ}>0\)。
• 当Q在三、四象限或y负轴上时，有\(\overrightarrow{OP}\times\overrightarrow{OQ}<0\)。
• 当Q在x轴上时，有\(\overrightarrow{OP}\times\overrightarrow{OQ}=0\)。
  

叉积的几何意义

• 叉积的值等于两条向量构成的平行四边形的面积，也等于两条向量构成的三角形的面积的两倍。

各种关系

判断点与直线的关系

• 当点O在直线PQ上时有\(\overrightarrow{OP} × \overrightarrow{OQ} = 0\)。

判断点与线段的关系

• 点O应该在直线PQ上且在直线上PQ对应的范围内，即横纵坐标都在PQ之间。

判断直线与直线的关系

• 平行时有\(\overrightarrow{PQ} × \overrightarrow{AB} = 0\)。
• 如果两条直线平行，再从一条直线上任取一点，检查是否在另一条直线上，由此判断共线。

计算直线的交点

• 首先判断直线是否刚好有一个交点。
• 令AB与PQ的交点为O，则\(|PO| : |PQ| = S_{△PAB} : S_{△PAB} + S_{△QAB}\)。
• 根据P和Q的坐标以及面积比，可以算出O的坐标。
• 线段AB和PQ可能没有交点，导致面积为负，需要使用叉乘。
  
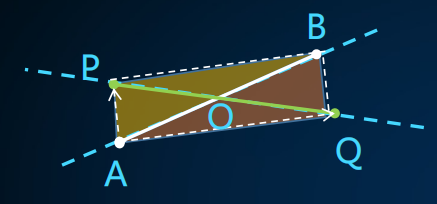
• 算面积时，就当作是上图这种正常情况下用叉乘求面积就可以了，上图这种正常情况下算出的面积应当都是正的。

判断点与简单多边形的关系：射线法

• 从点向右作出一条射线，判断与多边形的交点数量。
• 考虑点沿着射线移动，每产生一个交点，将会切换在多边形内外的状态。
  • 交点数量为偶数，则点在多边形外；
  • 交点数量为奇数，则点在多边形内。
  • 需要特判在边上的情况。

缺陷

• 射线与多边形相交在顶点时，不确定是否会改变状态。
• 射线可能经过一条共线的边，此时交点的数量有无限个。

改进策略

• 水平的边不影响状态的变化，可以忽略。
• 经过顶点改变状态时，该顶点必然分别是关联的两条边的上端点和下端点。所以忽略所有非水平边的上端点/下端点即可。

判断点与凸多边形的关系

• 逆时针检查多边形的每一条边。
  • 如果点在任意边的右侧，则在多边形的外部。
  • 否则，如果在任意边所在的直线上，则在该条边上。
  • 否则，在多边形的内部。

计算简单多边形的面积

• 任选参照点O，可以确定一条由任意点P发出的射线。通常直接选原点。
  • 如果点P在多边形内，则射线与多边形的交点数量为奇数。
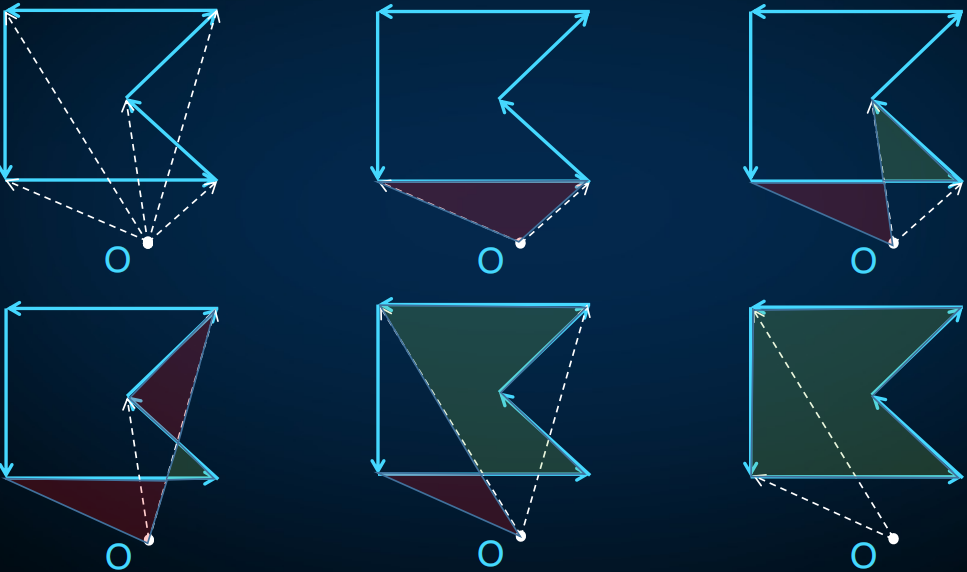
  • 每次与多边形相交，O与相交的边都可以确定一个包含P的三角形，且相交的边一定在射线的两边交替横跨。
• 所以左旋时认为三角形的面积为正，右旋时为负。
• 那么累加所有三角形的面积，则P刚好被计算一次。

那计算简单多边形的面积就需要逆时针检查多边形的每一条边，与参照点O形成的三角形的面积和就是多边形的面积（如果从这条边的起点到终点是左旋时认为三角形的面积为正，右旋时为负）。