NOIp模拟2 模拟退火 笔记

正好昨天学了模拟退火，就来写个笔记……

模拟退火，顾名思义就是模拟退火（看不懂不用担心，模拟退火和退火关系不大……）。

啥意思？

借用哦哎wiki上的图：

;

其实就是随机改变当前方案，根据答案是否增加决定是否真的改方案。随着时间增加，改变幅度越来越小。最终求得的大概率就是最优方案。

有点难理解……没关系我们手模一下过程

0.定义变量

T0：初始温度

T：当前温度（温度越高，改变幅度越大）

K：降温系数

T1：最终温度（当温度达到T1时break）

1.生成新解

一般根据当前温度的大小，在当前解的基础上随机生成一种新的方案。温度越大，新解与当前解的差异越大。

2.决定是否取新解

设红线表示当前解，蓝线表示随机生成的新解

v表示新解价值，u表示当前解价值。

如图所示，若v高于u，显然一定用新解代替当前解。

但如果v不高于u呢？

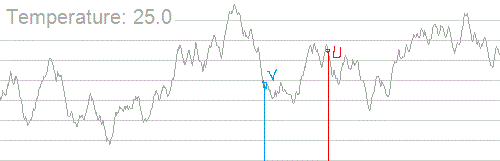
图中v<u,但v离最优解更近，所以取新解更合适。不能直接判断是否该取新解，所以应该有一定概率在v<u的情况下取新解。

这个概率为： \(e^{(v-u)/rT}\) ，其中 r 为任意正实数，根据题目不同自行修改。

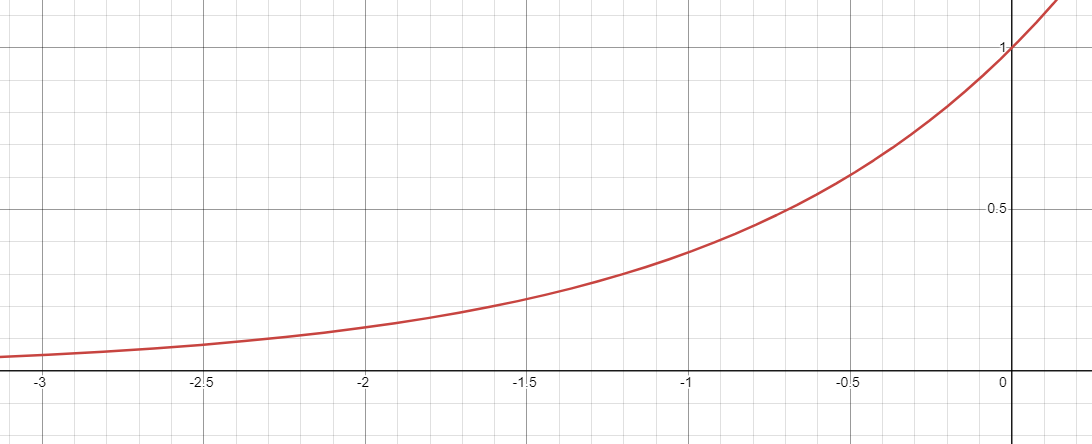
图为 \(y=e^x\) 的函数图像。可以观察到，当 \((v-u)/rT\) 小于0时， \(e^{(v-u)/rT}\) 在区间 \((0,1)\) 之间，且 v 与 u 的差越小， \(e^{(v-u)/rT}\) 越接近1，正好符合我们的需要。(其实所有 \(y=n^x\) 的图像全都是这种形状……这里把e换成别的常数也不是不行，不过前人用的全都是e……)

\(e^x\) 在c++中可以通过函数 exp(x) 快速求得。

综上所述：

若v>u，则一定用新解代替原解。

否则，有 \(e^{(v-u)/rT}\) 概率用新解代替原解。

3.降温

这一步容易理解，令T=T*K即可。

代码

const int T0=500;
const double K=0.996;
const double T1=0.1;
int ans=0;
int SA(){
	double T=T0;
	int u=ans; 
	while(T>T1){
		//生成解 
		（生成一个新解）
		int v=（新解价值） ;
		//判断是否取新解
		if(v>u||exp((v-u)/T)*32767>=rand()){
			//取新解
			(用新解代替原解)
			u=v;
		}
		T*=K;
	}
	return u; 
}

一些其他：

当时间充裕时可以多跑几遍模拟退火取最优值。

一遍模拟退火结束后，可以根据最终解生成几个变化幅度较小的解，取最优值。

模拟赛T3代码

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
int w[10],h[10];
int x[10],y[10];
int nx[10],ny[10];
int rd(int x,int y){
	if(x>y){
		return 1;
	}
	return rand()%(y-x+1)+x;
}
int summon(double T){
	for(int i=1;i<=k;i++){
		int X=T*(n-w[i]+1);
		nx[i]=x[i]+rd(-X,X);
		X=T*(m-h[i]+1);
		ny[i]=y[i]+rd(-X,X);
		nx[i]=max(nx[i],1);
		ny[i]=max(ny[i],1);
		nx[i]=min(nx[i],n-w[i]+1);
		ny[i]=min(ny[i],m-h[i]+1);
	}
	int res=0;
	int mp[105][105]={};
	for(int i=1;i<=k;i++){
		for(int j=0;j<w[i]&&nx[i]+j<=n;j++){
			for(int o=0;o<h[i]&&ny[i]+o<=m;o++){
				mp[nx[i]+j][ny[i]+o]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(mp[i][j]){
				res++;
			}
		}
	}
	return res;
}
int check(){
	for(int i=1;i<=k;i++){
		int X=2;
		nx[i]=x[i]+rd(0,X);
		ny[i]=y[i]+rd(0,X);
		nx[i]=max(nx[i],1);
		ny[i]=max(ny[i],1);
		nx[i]=min(nx[i],n-w[i]+1);
		ny[i]=min(ny[i],m-h[i]+1);
	}
	int res=0;
	int mp[105][105]={};
	for(int i=1;i<=k;i++){
		for(int j=0;j<w[i]&&nx[i]+j<=n;j++){
			for(int o=0;o<h[i]&&ny[i]+o<=m;o++){
				mp[nx[i]+j][ny[i]+o]=1;
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(mp[i][j]){
				res++;
			}
		}
	}
	return res;
}
const int T0=5;
const double K=0.9997;
const double T1=0.01;
int ans=0;
int SA(){//模拟退火 
	double T=T0;
	int u=0; 
	while(T>T1){
		int v=summon(T);
		if(v>u||exp((v-u)/T)*32767>=rand()){
			u=v;
			for(int i=1;i<=k;i++){
				x[i]=nx[i];
				y[i]=ny[i];	
			} 
		}
		T*=K;
		ans=max(ans,u);
	}
	ans=max(ans,check());
	ans=max(ans,check());//根据所得解生成2个新解，取其中最优 
	return u; 
}
int main()
{
	srand(114514);
	freopen("posters.in","r",stdin);
	freopen("posters.out","w",stdout);
	cin>>n>>m>>k;
	for(int i=1;i<=k;i++){
		cin>>w[i];
	}
	for(int i=1;i<=k;i++){
		cin>>h[i];
		x[i]=1;
		y[i]=1;
	}
	SA();
	SA();
	SA();//跑4遍模拟退火，增大最优解可能性 
	SA();
	cout<<ans<<endl;
	return 0;
}