实用指南:数据结构 实现二叉搜索树与哈希表
在数据结构中,二叉搜索树与哈希表都是查询效率非常高的结构!非常值得我们去学习,而且Java中的map和set的底层实现都与它们有关,学习它们有助于我们理解map和set的特性。
1. 二叉搜索树是什么?
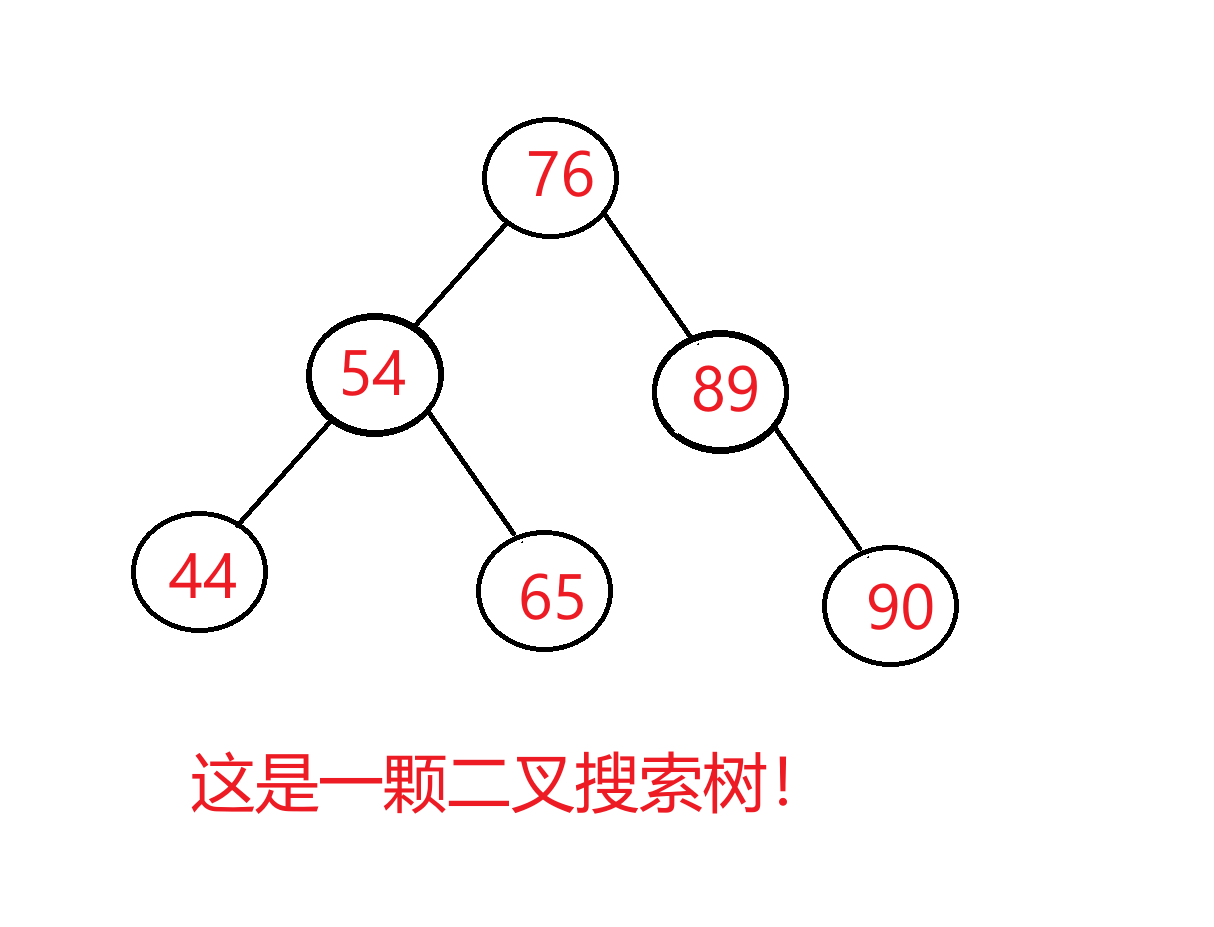
二叉搜索树是一种二叉树,它也称为二叉排序树,它可以是一颗空树,也可以是满足以下性质的二叉树:
- 如果它的左子树不为空,那么左子树上所有的结点的值都小于根结点的值。
- 如果它的右子树不为空,那么右子树上所有的结点的值都大于根结点的值。
- 它的左右子树也是二叉搜索树。
举个例子如下:

2. 手动实现二叉搜索树
二叉搜索树应该包含的方法:
- 查找(find)
- 插入(insert)
- 删除(delete)
2.1 方法——查找
要求:给定一个值key,在二叉搜索树中进行查找,如果树中有值为key的结点,就返回一个true,否则返回false。
思路:基于二叉搜索树的性质,如果根结点不为空,并且根结点的值不为key,key如果大于根结点的值,那么就去右子树中找,否则就去左子树中找。
在实现这个方法之前,先把必要的东西实现:
树结点:
public class BinarySearchTree {
static class TreeNode {
int key;
TreeNode left;
TreeNode right;
public TreeNode(int key) {
this.key = key;
}
}
//二叉搜索树的根结点
private TreeNode root;
}给定一颗二叉搜索树:
public void createTree() {
TreeNode node1 = new TreeNode(76);
TreeNode node2 = new TreeNode(54);
TreeNode node3 = new TreeNode(89);
TreeNode node4 = new TreeNode(44);
TreeNode node5 = new TreeNode(65);
TreeNode node6 = new TreeNode(90);
node1.left = node2;
node1.right = node3;
node2.left = node4;
node2.right = node5;
node3.right = node6;
root = node1;
}有了树结点和例子之后,就可以写查找方法了。
public boolean find(int key) {
TreeNode cur = root;
while (cur != null) {
if (cur.key == key) {
return true;
}else if (cur.key < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return false;
}进行测试:
public class Test {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.createTree();
boolean flag = binarySearchTree.find(65);
System.out.println(flag);
}
}
//运行结果
true符合预期!
2.2 方法——插入
要求:在二叉搜索树中插入一个新的结点,为了告诉我们是否插入成功,可以令它的返回值为boolean类型,插入成功就返回true,否则返回false。
思路:可以分为2种情况:
1.一开始树就为空树,即root == null,那么这时候直接插入即可。
2.一开始树不为空,并且树中已经有结点的值等于新结点时,直接返回false,否则我们就需要按照二叉搜索树的逻辑关系去找插入位置,然后才能插入新结点,画图说明如下:
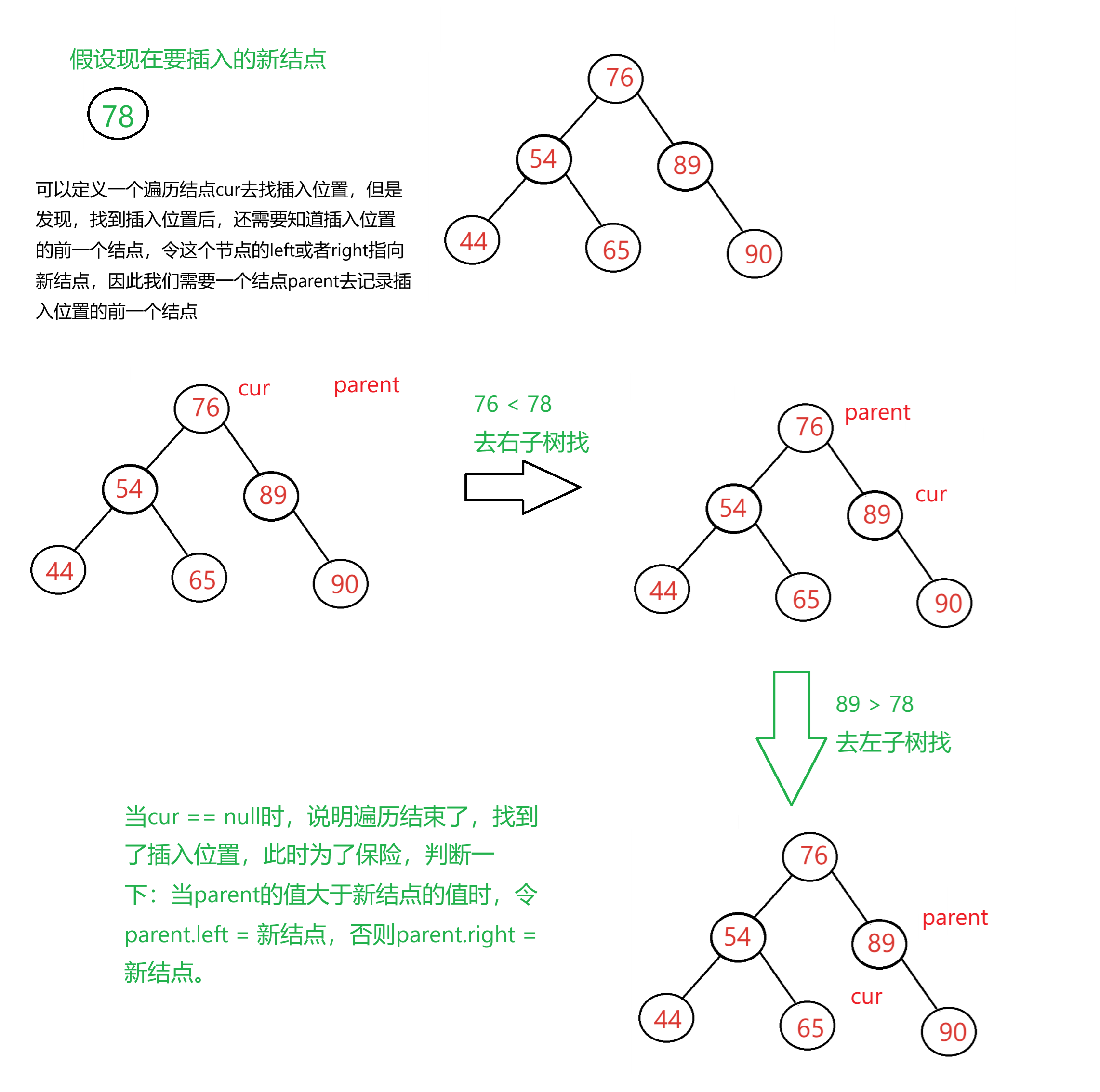
代码实现:
public boolean insert(int key) {
//一开始树为空
if (root == null) {
TreeNode node = new TreeNode(key);
root = node;
return true;
}
//一开始树不为空
TreeNode cur = root; //遍历结点
TreeNode parent = null; //插入位置的前一个结点
while (cur != null) {
//当树存在和新结点的值相同的结点
if (cur.key == key) {
return false;
}
//找插入位置
if (key > cur.key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//找到插入位置后
TreeNode node = new TreeNode(key);
if (key > parent.key) {
parent.right = node;
return true;
}else {
parent.left = node;
return true;
}
}进行测试:
public class Test {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.createTree();
boolean flag = binarySearchTree.insert(78);
System.out.println(flag);
}
}
//运行结果
true保险一点,通过调试可以看到
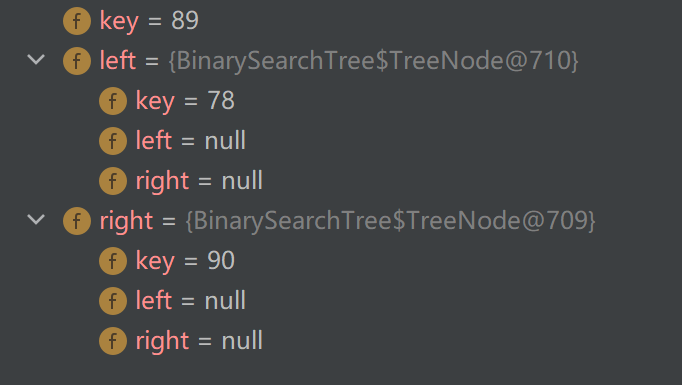
78这个新结点确实是插入到了89的左子树上,符合我们的预期!
2.3 方法——删除
要求:按照我们的需要,删除树中的一个结点,删除成功返回true,否则返回false。
思路:认真思考,发现删除可能出现的情况就以下几种(令待删除的结点为cur,它的双亲结点为parent):
1.一开始树为空,那么我们就没法删除。
2.一开始树不为空,但是没有我们要删除的结点,那也没法删除。
3.一开始树不为空,找到待删除结点了,并且它的左右子树都为空。
4..一开始树不为空,找到待删除结点了,但是待删除结点的左子树为空,右子树存在。
5.一开始树不为空,找到待删除结点了,但是待删除结点的右子树为空,左子树存在。
6.一开始树不为空,找到待删除结点了,但是待删除结点的左右子树都存在。
对于这几种情况,前3种很好处理,需要思考怎么处理的是后3种,画图分析比较直观:
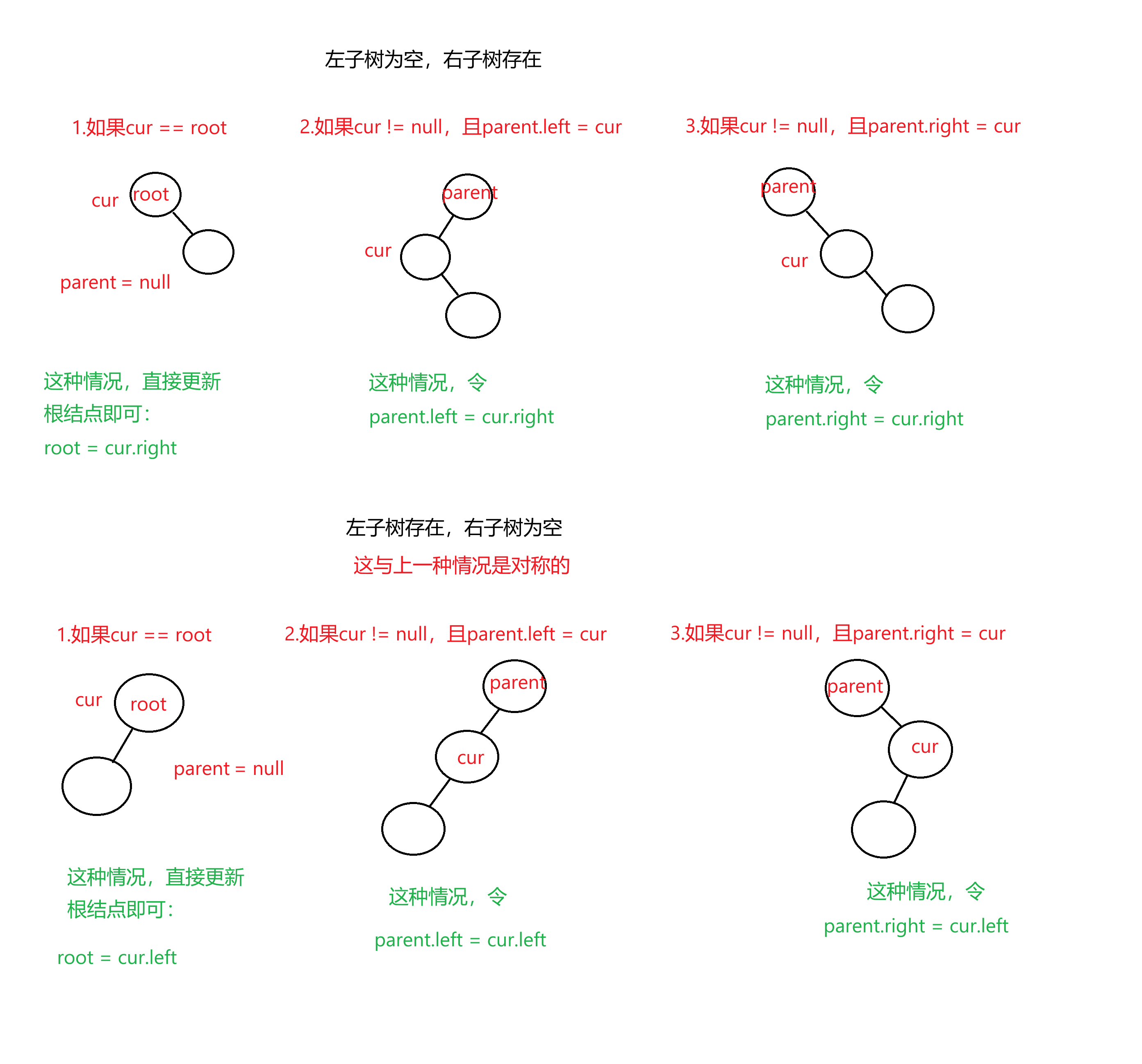

将所有情况理清楚之后,代码实现如下:
public boolean remove(int key) {
//如果树为空树
if (root == null) {
return false;
}
//树不为空的情况
TreeNode cur = root;
TreeNode parent = null;
//去找待删除结点
while (cur != null) {
if (cur.key == key) {
break;
}else if (key > cur.key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//如果cur == null,说明这棵树没有要删除的结点
if (cur == null) {
return false;
}
//找到待删除结点后
if (cur.left == null && cur.right == null) {
if (cur == root) {
root = null;
}else if (parent.left == cur) {
parent.left = null;
}else {
parent.right = null;
}
return true;
}else if (cur.left != null && cur.right == null) {
if (cur == root) {
root = cur.left;
}else if (parent.left == cur) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
return true;
}else if (cur.left == null && cur.right != null) {
if (cur == root) {
root = cur.right;
}else if (parent.left == cur) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
return true;
}else {
TreeNode t = cur.right; //用来找替换值的结点
TreeNode tp = null; //t的父结点
//这里去找cur右子树的最小值
while (t.left != null) {
tp = t;
t = t.left;
}
//找到后,替换cur的值
cur.key = t.key;
//处理t
//防止t一开始就是最小值,而tp = null而引发的空指针异常
if (t == cur.right) {
if (t.right == null) {
cur.right = null;
}else {
cur.right = t.right;
}
}else {
if (t.right == null) {
tp.left = null;
}else {
tp.left = t.right;
}
}
return true;
}
}进行测试:
public class Test {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
binarySearchTree.createTree();
boolean flag = binarySearchTree.remove(54);
System.out.println(flag);
}
}
//运行结果
true保险起见,进行调试,查看删除值为54这个结点后的二叉搜索树:
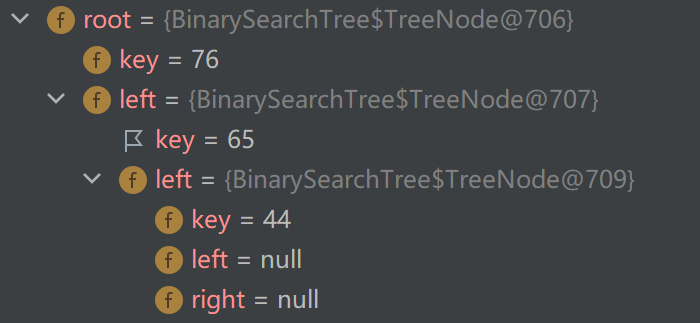
原来值为76的结点的左子树是54,现在变成了65,成功删除了值为54这个结点,符合我们的预期!
3. 二叉搜索树的性能分析
在实现插入和删除方法时,发现:这些操作都是在查找的基础上进行的,那么也就是说查找效率代表了二叉搜索树各种操作的性能!对于有n个结点的二叉搜索树,假如每个元素查找的概率相等,那么二叉搜索树的平均查找长度是一个关于结点在二叉搜索树的深度的函数,简单来说就是结点越深,比较的次数就越多。
最优情况:二叉搜索树为完全二叉树,那么其平均比较次数为:
最差情况:二叉搜索树为单分支树(也就是单链表),那么其平均比较次数为:
这里发现一个问题:如果二叉搜索树退化成了单分支树,它的性能就大大降低了,那么有没有什么数据结构不论按照什么次序插入和删除数据,它的性能都很好很稳定呢?有的,哈希表可以实现这个设想!
4. 什么是哈希表
哈希表(Hash Table),也称为散列表,是一种通过键(Key)直接访问存储位置的数据结构。它通过一个哈希函数(Hash Function) 将键映射到表中的某个索引位置,从而实现 O (1) 级别的平均查找、插入和删除效率。画图举例如下:
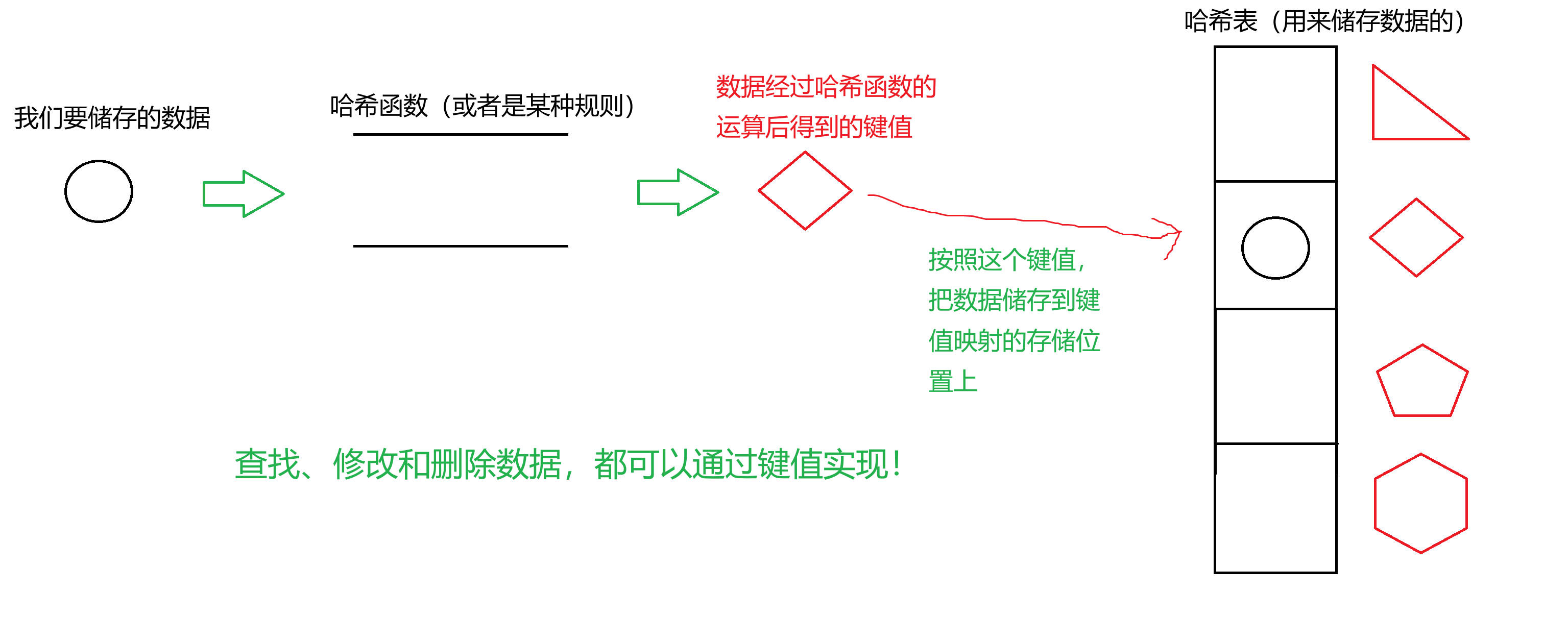
这样子看来,哈希表的性能十分强悍呢,但是事物没有十全十美的,哈希表会遇到一个叫冲突的问题。
冲突是什么?
当不同的数据通过相同的哈希函数计算后得到相同的键值(也可以叫哈希地址),这种现象称为哈希冲突或者哈希碰撞。并且将不同数据但是具有相同哈希地址的数据元素称为“同义词”。
我们知道存储空间是有限的,哈希表也不例外,实际要储存的数据量往往要大于哈希表的容量,这就说明,冲突的发生是必然的!我们能做的应该是降低冲突率。
降低冲突率的思路
想要降低冲突率,可以从两个角度出发:
- 设计合理的哈希函数
- 降低负载因子
1.设计合理的哈希函数
一个合理的哈希函数通常满足以下原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到 m-1 之间。
- 哈希函数计算出来的地址能均匀分布在整个空间中。
- 哈希函数应该比较简单。
因为设计哈希函数通常需要一定经验和对数据分布的理解,所以不建议初学者设计哈希函数。
常见的哈希函数如下:
1.直接定制法--(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B 优点:简单、均匀,缺点:需要事先知道关键字的分布情况使用场景:适合查找比较小且连续的情况。
2.除留余数法--(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数: Hash(key) = key% p(p<=m),将关键码转换成哈希地址。
3.平方取中法--(了解)
4.折叠法--(了解)
5.随机数法--(了解)
6.数学分析法--(了解)
2.降低负载因子
散列表的负载因子定义为:α = 填入表中的元素个数 / 散列表的长度
α 是散列表装满程度的标志因子。由于表长是定值,α 与 “填入表中的元素个数” 成正比,所以,α 越大,表明填入表中的元素越多,产生冲突的可能性就越大;反之,α 越小,标明填入表中的元素越少,产生冲突的可能性就越小。实际上,散列表的平均查找长度是载荷因子 α 的函数,只是不同处理冲突的方法有不同的函数。
对于开放定址法,负载因子是特别重要因素,应严格限制在 0.7 - 0.8 以下。超过 0.8,查表时的 CPU 缓存不命中(cache missing)按照指数曲线上升。因此,一些采用开放定址法的 hash 库,如 Java 的系统库限制了负载因子为 0.75,超过此值将 resize 散列表。
冲突率和负载因子的关系如下图所示:
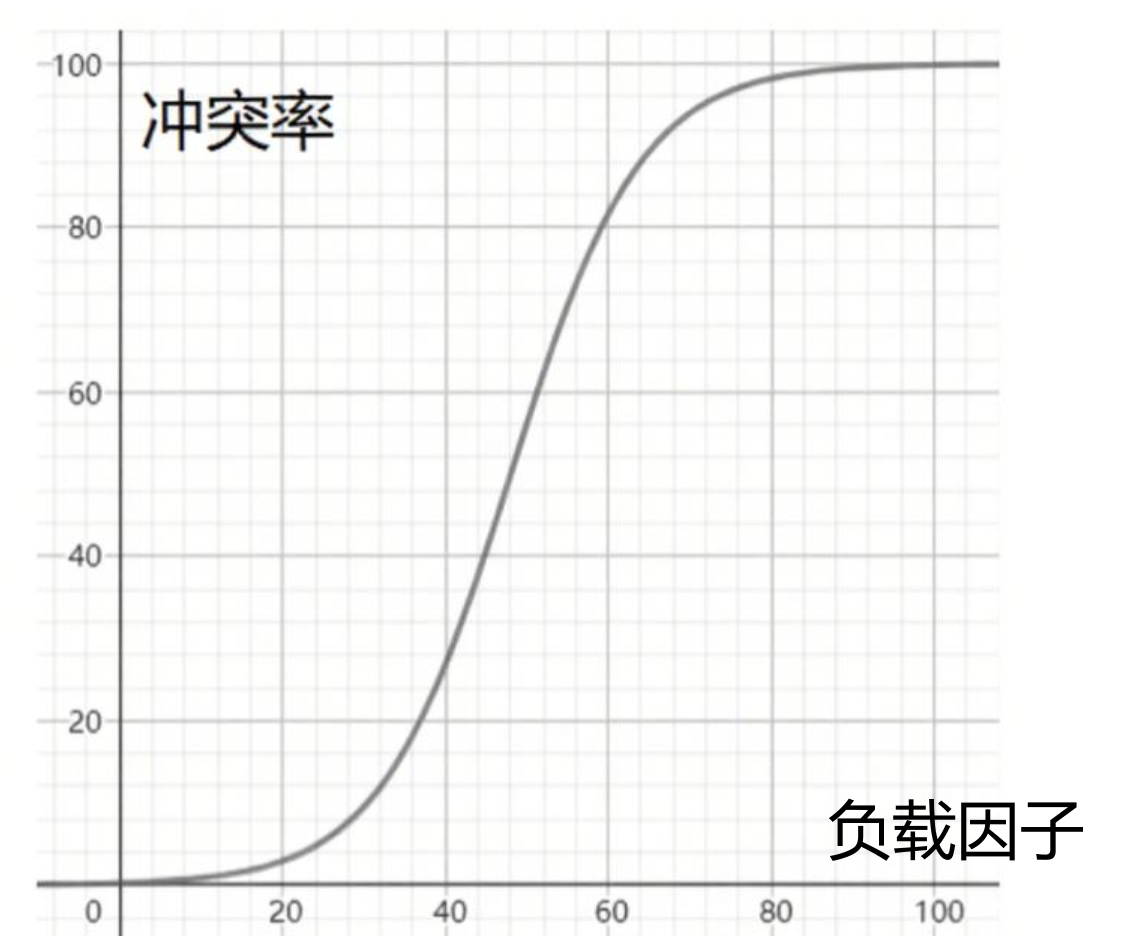
由图可知,当冲突率达到一个无法忍受的程度时,可以通过降低负载因子来变相地降低冲突率,而哈希表中已经储存的数据个数是不可变的,那么我们只能调整哈希表的容量了。
解决冲突的方式
解决哈希冲突有两种方式,一种是闭散列,另一种是开散列。
闭散列
闭散列也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以 把key存放到冲突位置中的“下一个” 空位置中去。那么现在问题是:这个空位置如何去找呢?
先举个例子:

现在我们要插入新元素44,通过图中的哈希函数计算,得到哈希地址 = 4,发现发生了哈希冲突,因为4下标的位置上已经插入了元素4,这时候哈希表还有空位置,那么就从冲突发生的位置开始向后探测,一直找到下一个空位置为止,这也就是所谓的线性探测了。那么44应该插入8下标的位置

但是线性探测的缺点也很明显:就是产生冲突的数据会堆积在一块,毕竟找空位置的方法是挨个向后找的,为了避免这个问题,二次探测就来了。
二次探测找空位置的方法: % m,或者
% m,其中:i = 1,2,3... ,
是插入数据通过哈希函数计算后的哈希地址,m为表的大小。
对于刚才要插入44的情况,会发生冲突,计算得= 4,那么
= (4 + 1^2) % 10 = 5,但是此时5下标已经有数据了,再次发生冲突,那么再次计算
= (4 + 2^2) % 10 = 8,此时8下标还空着,也就是找到空位置了!
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容。
闭散列的注意事项:
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,因为这会影响其他元素的搜索。比如说:删除元素4,那么44的查找可能会出现问题,如果非要删除的话,应该采用伪删除的方法。比散列最大的缺陷就是空间利用率比较低,但是这也是哈希的缺陷。
开散列/哈希桶(重点)
开散列法又叫链地址法(开链法),它是这样操作的:首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。那么刚才的例子就可以变成这样:

从这个图可以看出,开散列中的每个桶中放的都是发生哈希冲突的元素。开散列的思想简单来说就是将在大集合中做搜索的问题转换为在小集合中做搜索的问题。
如果小集合的搜索的冲突严重了,那么可以按照开散列的思想,把小集合的搜索转化为更小集合的搜索,比如说:
- 每个哈希桶的背后再是一张哈希表
- 每个哈希桶的背后是一颗搜索树
5. 手动实现哈希表
这里的实现方式我们采用开散列的方式,鉴于是初学者,哈希表就用数组+链表的组合!
我们实现的哈希表的方法包括:插入、查找和删除。
5.1 方法——插入
首先,我们的哈希表是数组加链表的组合,那么应该有一个数组和链表的结点:
public class MyHashBucket {
static class Node {
int key;
Node next;
public Node(int key) {
this.key = key;
}
}
//初始容量默认为10
public Node[] arr = new Node[10];
}接着需要记录插入元素的个数和默认的负载因子:
public class MyHashBucket {
static class Node {
int key;
Node next;
public Node(int key) {
this.key = key;
}
}
//初始容量默认为10
private Node[] arr = new Node[10];
private int size; //当前插入的元素个数
private static final double DEFAULT_LOAD_FACTOR = 0.75; //默认的负载因子
}要求:往哈希表中插入一个元素。
思路:首先先根据插入的元素,计算出哈希地址,哈希函数可以使用除留余数法,然后根据哈希地址找到指定的哈希桶。由于每个桶都是一个链表,并且哈希表中通常没有重复的数据,那么如果这个桶的头节点不为空,先遍历一下这个链表,如果没有与插入元素重复的元素,就头插插入元素,如果有就结束方法;如果一开始这个桶的头节点就是空的,直接头插就行,同时size++。
当我们成功插入元素后,需要判断一下是否需要扩容,如果此时哈希桶的负载因子大于或者等于默认负载因子,就需要扩容了(为了降低冲突率),而扩容正是插入操作的难点,重点分析扩容。
扩容操作并不能简单的复制数组,因为当数组的长度发生变化后,原数组中的数据的哈希地址可能会发生变化,那么这就需要把它放到新的桶里去了,例如:假如原数据12,它在原数组的哈希地址是12%10 = 2,而当数组扩容两倍后,它在新数组的哈希地址为12%20 = 12,发生变化!所以扩容的核心思路就是遍历原哈希表中的每个数据,再计算它们在新哈希表的哈希地址,根据新的哈希地址放到新的桶里去。
那么代码实现如下:
public void insert(int key) {
//计算哈希地址,使用Math,abs()方法是为了防止插入值是负数的情况!
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
//开始遍历,查看哈希表是否有重复
while (cur != null) {
if (cur.key == key) {
return;
}
cur = cur.next;
}
//哈希表没有重复
//进行头插,即使一开始为空链表也可以
Node node = new Node(key);
node.next = arr[index];
arr[index] = node;
size++;
//判断是否需要扩容
if (doLoadFactor() >= DEFAULT_LOAD_FACTOR) {
resize();
}
}
//求当前哈希表负载因子
private double doLoadFactor() {
return size*1.0/arr.length;
}
//扩容操作
private void resize() {
Node[] newArr = new Node[2*arr.length];
//遍历原哈希表的每一个元素,并放入新的哈希表中
for (int i = 0; i < arr.length; i++) {
Node cur = arr[i];
while (cur != null) {
//计算新的哈希地址
int newIndex = Math.abs(cur.key) % newArr.length;
//保存cur的下一个位置
Node curN = cur.next;
//将cur放入新的哈希表中的桶
cur.next = newArr[newIndex];
newArr[newIndex] = cur;
cur = curN;
}
}
//更新哈希表
arr = newArr;
}进行测试:
public class Test {
public static void main(String[] args) {
MyHashBucket hashBucket = new MyHashBucket();
hashBucket.insert(12);
}
}进行调试,发现哈希表里成功插入了12这个数据,符合预期。
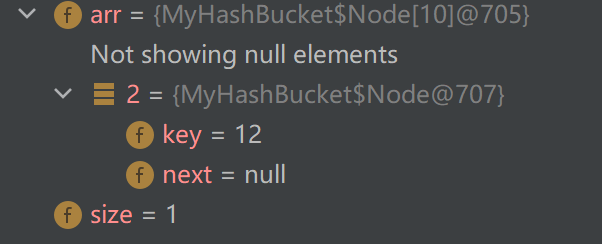
5.2 方法——查找
要求:给定一个值,去哈希表中查找,找到了返回true,否则返回false。
思路:其实刚才实现插入操作的时候,已经变相地实现查找操作了,查找其实也就是根据哈希地址找到对应的桶,去桶里遍历就好了。
代码实现如下:
public boolean find(int key) {
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
while (cur != null) {
if (cur.key == key) {
return true;
}
cur = cur.next;
}
return false;
}进行测试:
public class Test {
public static void main(String[] args) {
MyHashBucket hashBucket = new MyHashBucket();
hashBucket.insert(12);
System.out.println(hashBucket.find(13));
System.out.println(hashBucket.find(12));
}
}
//运行结果
false
true符合预期!
5.3 方法——删除
要求:给点一个值,去哈希表中删除与这个值一样的数据,成功删除返回true,否则返回false。
思路:还是老样子,先根据给定的值,计算出哈希地址,找到指定的哈希桶,接着去遍历桶里的链表,找到后,就按照删除链表节点的方式即可,找不到的话,就说明哈希表没有这个数据,直接返回false,记得要size--。
代码实现如下:
public boolean remove(int key) {
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
Node prev = null; //记录cur的前一个节点
while (cur != null) {
if (cur.key == key) {
break;
}
prev = cur;
cur = cur.next;
}
//cur == null说明哈希表没有这个元素
if (cur == null) {
return false;
}
//如果要删除的值位于头节点
if (cur == arr[index]) {
arr[index] = cur.next;
size--;
return true;
}
//位于尾节点和中间节点的情况:
prev.next = cur.next;
size--;
return true;
}进行测试:
public class Test {
public static void main(String[] args) {
MyHashBucket hashBucket = new MyHashBucket();
hashBucket.insert(1);
hashBucket.insert(2);
hashBucket.insert(3);
System.out.println(hashBucket.remove(1));
System.out.println(hashBucket.remove(4));
}
}
//运行结果
true
false进行调试,发现:
删除1前:
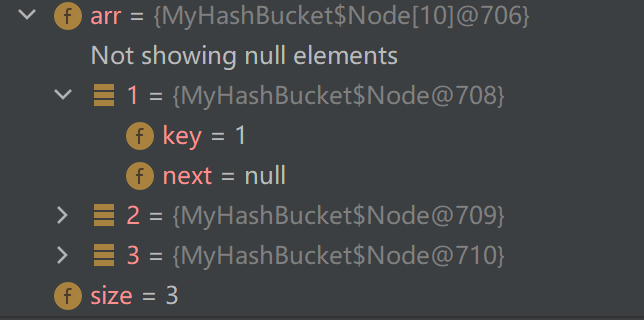
删除1后:
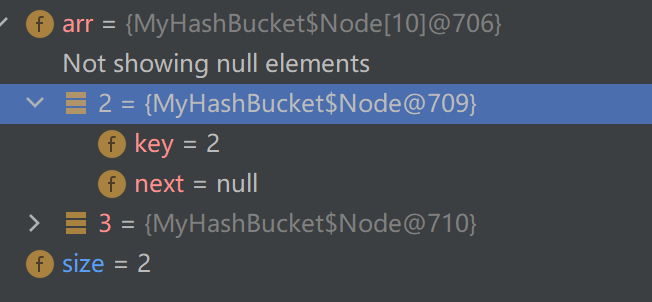
1成功被删除,符合预期!
6. 哈希表的性能分析
虽然哈希表一直在和冲突做斗争,但在实际使用过程中,我们认为哈希表的冲突率是不高的,冲突个数是可控的,也就是每个桶中的链表的长度是一个常数,所以,通常意义下,我们认为哈希表的插入/删除/查找时间复杂度是 O(1) 。
到此,二叉搜索树与哈希表成功实现!
完整代码
二叉搜索树:
public class BinarySearchTree {
static class TreeNode {
int key;
TreeNode left;
TreeNode right;
public TreeNode(int key) {
this.key = key;
}
}
//二叉搜索树的根结点
private TreeNode root;
public void createTree() {
TreeNode node1 = new TreeNode(76);
TreeNode node2 = new TreeNode(54);
TreeNode node3 = new TreeNode(89);
TreeNode node4 = new TreeNode(44);
TreeNode node5 = new TreeNode(65);
TreeNode node6 = new TreeNode(90);
node1.left = node2;
node1.right = node3;
node2.left = node4;
node2.right = node5;
node3.right = node6;
root = node1;
}
public boolean find(int key) {
TreeNode cur = root;
while (cur != null) {
if (cur.key == key) {
return true;
}else if (cur.key < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return false;
}
public boolean insert(int key) {
//一开始树为空
if (root == null) {
TreeNode node = new TreeNode(key);
root = node;
return true;
}
//一开始树不为空
TreeNode cur = root; //遍历结点
TreeNode parent = null; //插入位置的前一个结点
while (cur != null) {
//当树存在和新结点的值相同的结点
if (cur.key == key) {
return false;
}
//找插入位置
if (key > cur.key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//找到插入位置后
TreeNode node = new TreeNode(key);
if (key > parent.key) {
parent.right = node;
return true;
}else {
parent.left = node;
return true;
}
}
public boolean remove(int key) {
//如果树为空树
if (root == null) {
return false;
}
//树不为空的情况
TreeNode cur = root;
TreeNode parent = null;
//去找待删除结点
while (cur != null) {
if (cur.key == key) {
break;
}else if (key > cur.key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//如果cur == null,说明这棵树没有要删除的结点
if (cur == null) {
return false;
}
//找到待删除结点后
if (cur.left == null && cur.right == null) {
if (cur == root) {
root = null;
}else if (parent.left == cur) {
parent.left = null;
}else {
parent.right = null;
}
return true;
}else if (cur.left != null && cur.right == null) {
if (cur == root) {
root = cur.left;
}else if (parent.left == cur) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
return true;
}else if (cur.left == null && cur.right != null) {
if (cur == root) {
root = cur.right;
}else if (parent.left == cur) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
return true;
}else {
TreeNode t = cur.right; //用来找替换值的结点
TreeNode tp = null; //t的父结点
//这里去找cur右子树的最小值
while (t.left != null) {
tp = t;
t = t.left;
}
//找到后,替换cur的值
cur.key = t.key;
//处理t
//防止t一开始就是最小值,而tp = null而引发的空指针异常
if (t == cur.right) {
if (t.right == null) {
cur.right = null;
}else {
cur.right = t.right;
}
}else {
if (t.right == null) {
tp.left = null;
}else {
tp.left = t.right;
}
}
return true;
}
}
}哈希表:
public class MyHashBucket {
static class Node {
int key;
Node next;
public Node(int key) {
this.key = key;
}
}
//初始容量默认为10
private Node[] arr = new Node[10];
private int size; //当前插入的元素个数
private static final double DEFAULT_LOAD_FACTOR = 0.75; //默认的负载因子
public void insert(int key) {
//计算哈希地址,使用Math,abs()方法是为了防止插入值是负数的情况!
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
//开始遍历,查看哈希表是否有重复
while (cur != null) {
if (cur.key == key) {
return;
}
cur = cur.next;
}
//哈希表没有重复
//进行头插,即使一开始为空链表也可以
Node node = new Node(key);
node.next = arr[index];
arr[index] = node;
size++;
//判断是否需要扩容
if (doLoadFactor() >= DEFAULT_LOAD_FACTOR) {
resize();
}
}
//求当前哈希表负载因子
private double doLoadFactor() {
return size*1.0/arr.length;
}
//扩容操作
private void resize() {
Node[] newArr = new Node[2*arr.length];
//遍历原哈希表的每一个元素,并放入新的哈希表中
for (int i = 0; i < arr.length; i++) {
Node cur = arr[i];
while (cur != null) {
//计算新的哈希地址
int newIndex = Math.abs(cur.key) % newArr.length;
//保存cur的下一个位置
Node curN = cur.next;
//将cur放入新的哈希表中的桶
cur.next = newArr[newIndex];
newArr[newIndex] = cur;
cur = curN;
}
}
//更新哈希表
arr = newArr;
}
public boolean find(int key) {
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
while (cur != null) {
if (cur.key == key) {
return true;
}
cur = cur.next;
}
return false;
}
public boolean remove(int key) {
int index = Math.abs(key) % arr.length;
Node cur = arr[index];
Node prev = null; //记录cur的前一个节点
while (cur != null) {
if (cur.key == key) {
break;
}
prev = cur;
cur = cur.next;
}
//cur == null说明哈希表没有这个元素
if (cur == null) {
return false;
}
//如果要删除的值位于头节点
if (cur == arr[index]) {
arr[index] = cur.next;
size--;
return true;
}
//位于尾节点和中间节点的情况:
prev.next = cur.next;
size--;
return true;
}
}感谢您的阅读,如有错误,还请指出,谢谢!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号