题解：P8879 『STA - R1』Crossnews

题目分析

看见别的题解都在数形结合去理解，感觉都好强啊，但是实际上这题硬拆就能证明了。

注意到

\[\begin{aligned} \sum_{i = 1}^{n} b_i(b_i-a_i) &= (b_i- \frac{1}{2} a_i)^2 - \frac{1}{4} a_i^2 & \\ &= \sum_{i=1}^{n} (b_i- \frac{1}{2} a_i)^2 - \sum_{i=1}^{n} \frac{1}{4} a_i^2 & \\ \end{aligned} \]

其中 \(\sum_{n}^{i=1} \frac{1}{4} a_i^2\) 是一个定值，不用考虑其大小，那么只需要考虑每个 \((b_i- \frac{1}{2} a_i)^2\) 和它们之间的相互关系即可。

显然单独的 \((b_i- \frac{1}{2} a_i)^2\) 当且仅当 \(b_i=\frac{1}{2} a_i\) 时取到最小值 \(0\)。

那么考虑相互关系，假定我们已经知道了 \(b_i\) 的值，因为 \(a_i\) 与 \(a_{i+1}\) 的关系不确定，所以分两类讨论。

case 1：\(a_{i+1} \ge \frac{1}{2}a_i\)

那显然 \(b_{i+1} = \frac{1}{2} a_{i+1}\) 此时和 \(b_{i+1} \ge b_i\) 不冲突，直接取即可，这也就是 \(10\) 分性质分的思路了。

case 2：\(a_{i+1} < \frac{1}{2}a_i\)

此时的 \(b_i\) 就是 \(b_{i+1}\) 的下界（不是 mc 里的那个）。

这里有两种考虑方式，分别是图形（当然没那么复杂）和代数，都好理解，都能证明此时 \(b_{i+1}=b_i\)。

（点击蓝字可直接跳转）。

图形法

把他们的值当横坐标画图，长这样

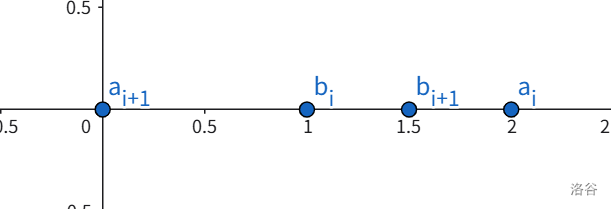
那么原式就表示 \(a_i\) 到 \(b_i\)，\(a_{i+1}\) 到 \(b_{i+1}\) 的距离平方和，显然 \(b_i\) 固定时 \(b_{i+1}=b_i\) 是最优的。

代数法

因为 \(b_{i+1} \ge b_i\)， 所以放缩一下可以得到

\[\begin{aligned} (b_i- \frac{1}{2} a_i)^2 + (b_{i+1}- \frac{1}{2} a_{i+1})^2 \ge (b_i- \frac{1}{2} a_i)^2 + (b_i- \frac{1}{2} a_{i+1})^2 \end{aligned} \]

当且仅当 \(b_{i+1}=b_i\) 时成立。

推广

推广到规模为 \(n\) 的，可以得到 \(b_1=b_2=\dots=b_n=b\)，则

\[\begin{aligned} \sum_{i=1}^{n} (b- \frac{1}{2} a_i)^2 &= n b^2 - b \sum_{i=1}^{n}a_i + \frac{1}{4} \sum_{i=1}^{n} a_i^2 \end{aligned} \]

这是一个二次函数，当且仅当 \(b=\frac{\sum_{i=1}^{n}a_i}{2n}=\frac{1}{n}\sum_{i=1}^n \frac{a_i}{2}\) 时取最小值（因为 \(n>0\)）。

不难发现 \(b\) 是个平均值，那么平均值的性质就能用了。

总结

如果你按照上述思路去写了，你会发现，考虑 \(a_i\) 之间的大小关系有点难写，但是 \(b_i\) 看起来更好写。

再次观察上述思考，发现一个区间内 \(b_i\) 都相等，考虑转化为区间合并，最后若干区间的这个 \(b_i\) 序列不减即可。

要是减了（\(b_{i+1}<b_i\)）怎么办呢？

好说，直接合并区间 \(i\) 和 \(i+1\) 就行了，这样 \(b_i\) 也会变小（从平均值角度理解即可），对后面 \(b_{i+k}\) 取更小的值也更有利，整体答案也能更小，所以到最后用单调栈维护几个区间的合并就行了。

代码实现

代码中的 ave 实际上就是 \(b\)。

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <stack>
#include <iomanip>
using namespace std;
#define ll long long
#define N 1000010
#define mod 1000000007
int n;
double ans, sum, b, a[N];
struct Intervals
{
	int len;
	double sum;
	Intervals(int len, double sum) : len(len), sum(sum) {}
	double get_ave()
	{
		return sum / len;
	}
	bool operator<(Intervals &another)
	{
		return get_ave() < another.get_ave();
	}
	void merge(Intervals &another)
	{
		len += another.len;
		sum += another.sum;
	}
};
stack<Intervals> st;
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; ++i)
		cin >> a[i];
	for (int i = 1; i <= n; ++i)
	{
		Intervals temp = {1, a[i]};
		while (st.size() && temp < st.top())
		{
			temp.merge(st.top());
			st.pop();
		}
		st.push(temp);
	}
	int i = n;
	while (st.size())
	{
		Intervals temp = st.top();
		double b = temp.get_ave() / 2;
		while (temp.len--)
			ans += b * (b - a[i--]);
		st.pop();
	}

	cout << std::fixed << std::setprecision(7) << ans << '\n';
	return 0;
}