P7824 「RdOI R3」毒水 题解

\(1\) 分的思路就不多说了，我们从 \(10\) 分开始看起。

初步思考——为啥刚好是 \(3\) 倍？

不难发现所给的 \(maxk\) 刚好是 \(n\) 的 \(3\) 倍，考虑每瓶水给 \(3\) 只老鼠喝，则每瓶水对应的 \(3\) 只老鼠有以下状态：

111，000，100，110。

对前两种来讲显然是没有变异鼠的，因为变异鼠肯定都是后两种——别人死，他活；别人活，他死。

所以我们可以知道：如果对于 \(1\) 瓶水有 \(2\) 个及以上的老鼠死了，那这瓶水就是有毒的。

初步优化——二进制的妙用

通过惊人的注意力可以发现 \(3\log_2 1000 \approx 30\)，诶这不刚好就是接下来的 \(30\) 分吗，啥东西有 \(\log_2\) 复杂度呢？二进制啊！

考虑每 \(3\) 只老鼠为一组，每组的编号为 \(i\)。让第 \(i\) 组去负责每瓶水中编号二进制第 \(i\) 位为 \(1\) 的水。

这样由每组死亡数大于等于 \(2\) 的就能确定：毒水对应编号的第 \(i\) 位一定是 \(1\)，最后可以组合出来所求毒水编号。

深层优化——再来一层二进制

我不知道子任务 4 的部分分怎么打。

可以发现老鼠用的还是太多了，考虑一开始只用每组一只老鼠去喝水。

然后再以类似的思路，去对每组进行二进制拆分，但每只老鼠喝水的编号应该变成其负责的老鼠喝水编号的异或和。

设第 \(i\) 只老鼠负责的水瓶编号是 \(m[i]\)，负责的老鼠编号是 \(b[i]\)，则上述计算可表述为

\[m[i]=\mathop{\oplus } \limits_{j\in b[i]}{m[j]} \]

最后再找一个老鼠把验证每组的老鼠同理验证一下。

以 \(1000\) 瓶水为例：

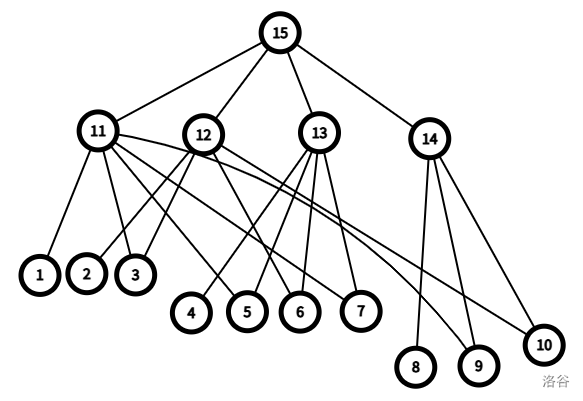
老鼠们之间的关系就长这样，是近似的一棵树。

定义鼠上鼠为非叶子结点的老鼠。

那么可以分为两种情况：

变异鼠在鼠上鼠里

一定且仅此时有：鼠上鼠的总死亡数为奇数。

证明：由于根结点是其他所有鼠上鼠的异或和，所以所有鼠上鼠喝的水肯定都被喝了偶数次，毒水肯定也只能毒死偶数只。但是变异鼠混了进来，要么变异鼠没喝到毒水死了，死亡数 \(+1\)，是奇数；要么变异鼠喝到毒水，死亡数 \(-1\)，也是奇数。

那么只要根据普通老鼠的死亡情况来推测即可。（做法同上 \(30\) 分做法，拼凑即可）。

变异鼠在普通鼠里

此时，对于有变异鼠的那个子树（不包含根结点），死亡数一定是奇数。证明也是同上的，要么死亡数 \(-1\)，要么死亡数 \(+1\)，都是奇数。

那我们只需要一个个看根结点以外的鼠上鼠和他下面的老鼠，如果这个鼠上鼠的子树内死亡数为奇数，就可以知道变异鼠编号的对应二进制位上此位为 \(1\)。把所有的累计起来，就能得到变异鼠编号。

最后把变异鼠的死亡状态反过来，跑一遍上种情况的代码即可。

代码实现

#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;
#define N 1010
int n, maxk, r[N];
int t1, t2;
// t1为普通老鼠的数量，t2为鼠上鼠的数量-1（因为不包含根结点）
int cnt[N], cntt[N];
vector<int> mouse[N];
int main()
{
    scanf("%d%d", &n, &maxk);
    if (n == 1)
    {
        putchar('2'), putchar('\n');
        fflush(stdout);
        putchar('1');
        return 0;
    }
    if (n == 2)
    {
        printf("1 1 1\n2\n");
        fflush(stdout);
        int res;
        scanf("%d", &res);
        printf("%d", 2 - res);
        return 0;
    }
    t1 = ceil(log2(n)), t2 = ceil(log2(t1));
    for (int i = 0; i < t1; ++i)
    {
        putchar('1'), putchar(' ');
        for (int j = 0; j < n; ++j)
            if ((j >> i) & 1)
                mouse[i].emplace_back(j + 1);
        printf("%d ", mouse[i].size());
        for (auto x : mouse[i])
            printf("%d ", x);
        putchar('\n');
    }

    for (int i = t1; i < t1 + t2; ++i)
    {
        for (int j = 1; j <= n; ++j)
            cnt[j] = 0;

        putchar('1'), putchar(' ');
        for (int j = 0; j < t1; ++j)
            if ((j >> (i - t1)) & 1)
                for (auto x : mouse[j])
                    ++cnt[x];//模拟异或，下面同理
        for (int j = 1; j <= n; ++j)
            if (cnt[j] & 1)
                mouse[i].emplace_back(j);

        printf("%d ", mouse[i].size());
        for (auto x : mouse[i])
            ++cntt[x], printf("%d ", x);
        putchar('\n');
    }
    putchar('1'), putchar(' ');
    for (int i = 1; i <= n; ++i)
        if (cntt[i] & 1)
            mouse[t1 + t2].emplace_back(i);
    printf("%d ", mouse[t1 + t2].size());
    for (auto x : mouse[t1 + t2])
        printf("%d ", x);
    putchar('\n'), putchar('2'), putchar('\n');
    fflush(stdout);
    for (int i = 0; i <= t1 + t2; ++i)
        scanf("%d", &r[i]), r[i] ^= 1;
    int flag = 0;
    for (int i = t1; i <= t1 + t2; ++i)
        flag ^= r[i];
    int ans = 0;
    if (!flag)
    {
        int super_mouse = 0;
        for (int i = t1; i < t1 + t2; ++i)
        {
            flag = r[i];
            for (int j = 0; j < t1; ++j)
                if ((j >> (i - t1)) & 1)
                    flag ^= r[j];
            if (flag)
                super_mouse ^= 1 << (i - t1);
        }
        r[super_mouse] ^= 1;
    }
    for (int i = 0; i < t1; ++i)
        if (r[i])
            ans ^= 1 << i;
    printf("%d\n", ans + 1);
    return 0;
}