四维之美
一. 四维空间初探
1.引子
1.1 一个正凸多胞体的演示程序:Tesseract
点这里下载(88k).点击右键进行预览和设置,如果喜欢,可以拷至Windows/system32目录下进行安装:)。在设置中可以选择是否播放背景音乐和多边形细分质量。如果阁下的电脑比曹丞相还过时的话,可以考虑将Polygon Quality设为Low以提高画面流畅度。
这是一个屏幕保护程序,演示了四维空间中的6个正凸多胞体:单形(Pentachoron),超立方体(Tesseract),正16胞体(Hexadecachoron),正24胞体(Icositetrachoron),120胞体(Hecatonicosachoron)和正600胞体(Hexacosichoron)。顺便想说一句,这些正凸多胞体的繁杂冗长而又晦涩难记的英文名又一次证明了英文中造词法的落后性,虽然它们并没有相对应的中文名(反正我google了半天也没找到)而只是简单的被称为正多少胞体。关于这些正凸多胞体的几何结构我会在下一篇文章中进行介绍。下面是该屏保的一张截图。

1.2 一些废话
说到四维的美,到底哪里美了?不知诸位中有没有能直接用线粒体来体味到这种美的数学Geek,有的话请跳出来给我们这些三维蛮荒生物参破参破。记得在当年的某节物理课上,也有某老师大肆吹嘘薛定鄂方程是多么美多么正点,我是把它正着看了又倒过来看也没发现美在何处,直到我把印有该方程的那一页书提起来对着阳光看,才发现果然很美,当然美的不是薛定鄂方程,而是从纸张中隐约透过来的某个mm。对于四维空间,我还是只能够眼来欣赏它的视觉美。所以本文并不从数学的角度来阐述四维空间的构造和性质,而是简单介绍一下四维物体的3d图形呈现。至于它到底美不美就由大家自行判断好了。
2.由三维到四维的扩展
我们知道,三维空间可以由一个三个轴的坐标系以及建立在此坐标系上的空间坐标点(x,y,z)来表述。相应的,我们可以在相象中构造出一个有着四个互相正交的轴的坐标系,在这个坐标系中,一个四维的点同样可以用一个坐标来表示,即(x,y,z,t)。当然,我们没有必要纠结这四个坐标轴到底是如何放置以形成两两垂直的,因为这在三维空间中并不存在。如果固定住四维空间某一个坐标分量,就得到了一个三维空间。在t轴中的每一点都对应着一个这样一个三维空间,所以四维空间可以被认为是由无穷多个平行的三维空间组成。这种将某一坐标分量固定从而得到低一维空间的方式可以叫做截面法(或许在这里称为截体法更为合适)。
3.四维物体的三维呈现
如果存在着像《GEB》书中所描述的“弹出煮调饮”,“推入小蜜酥”这样神奇的东西,那我们就可以在维度世界里尽情的畅游了。想看看四维生物长什么样?吃块推入四维空间小蜜酥就行,比挤公交去动物园还方便。然而事实是如此:我们生活在三维世界,所以永远也无法得到对四维世界的一个真实的认识。正如在艾舍儿的画作《爬虫》中生活在二维空间中的蜥蜴永远也无法得到直观的三维认识一样。作为安慰的是,有一些方法可以帮助我们间接的认识四维世界,比如上面提到的截面法就是其中一种,下面来介绍一种更为直观的方式,投影法。
3.1 四维物体的投影法
3.1.1 中心投影法
回忆一下我们是怎么在平面上表现三维物体的?答案是透视。学过美术的同学可能都知道透视法中的一点透视,两点透视(成角透视)和邪恶的三点透视(为什么邪恶可以参见当年的skyhits)。相应地,在四维空间中也可以构造出类似的透视法则。
在三维空间的透视法中,我们通常需要先选择一个视平面,位于这个平面中的物体可以按照原样直接画在白纸上,而不在这个平面中的物体则需要按照透视规则做出一定的形变。在观察这些扭曲在二维空间中的三维图形时,我们的三维空间想像能力可以帮助复原这些二维图像从而得到一个三维的视觉印象。当然,空间的想像能力是建立在大量充分的实际观察经验之上的,所以当我们看到投影在三维空间的四维图形时,只能观察到一个杂乱的三维结构,而无法将其还原成原本的四维结构。不过没关系,反正又不只是我一个人看不懂,大家都看不懂,zhuangbility的牛人除外。还是先来看看将四维物体投影到三维空间的中心投影法。
中心投影法其实理解起来很容易(复杂的我也理解不了),设想我们的眼晴位于四维空间中t轴的某一点(t=near),视线方向与与t轴平行,根据我们在三维空间中获取的经验:越远的物体看上去越小,平行于视线方向的直线最终会交于一点,在透视法中被称为灭点。类似地,在t轴上取一灭点(t=far), 那么投影关系可以用这个函数来表示:
1 Vector3D Vector4D::Project(float near, float far)
2 {
3 float bal = (far - t)/(far - near);
4 return Vector3D(x*bal, y*bal, z*bal);
5 }
其中bal实际上就是一个相似比例,在t=near处值为1,在t=far处值为0, 将x,y,z坐标分量分别乘上这个比例系数,就得到了投影在三维空间中的三维向量。
3.2.2 球极投影法
球极投影法是在四维空间中设一极点,通常是四维物体的某个顶点。依次从极点到四维物体上的每个点作一射线,射线与投影三维体的交点就是投影点。相对来说,三维空间中的球极投影法可能会更容易理解一些,可以看这里。
3.2 四维空间中的坐标变换
关于四维空间中的平移和缩放就不多说了,跟三维空间中的完全一样:坐标分量分别相加或是乘上一个放大系数就行了。在这里主要说一下四维空间中的旋转。在三维空间中有三种互相正交的旋转分量,分别是,xy平面中的旋转(即绕z轴旋转),yz平面中的旋转(即绕x轴旋转)和xz平面中的旋转(即绕y轴旋转)。在四维空间中,我们有6个互相正交的旋转分量,除了上述与三维空间相同的三个分量之外,还有在xt平面, yt平面, zt平面的旋转分量。在xt平面上的旋转也可以理解为绕yz平面的旋转,因为在旋转过程中,y,z坐标是固定不变的,而x,t坐标以2PI为周期变化。与三维空间的旋转相似,四维空间中的旋转也可以用一个矩阵来表示:

有了投影关系和坐标变换矩阵后,就可以进行四维物体的三维投影的绘制了,整个过程很简单:
1. 首先给定一个四维物体的几何信息,比如顶点位置,边,面等。
2. 给定一个旋转分量,计算出旋转矩阵。乘上初始的位置坐标,就得到变换后的四维空间坐标(x,y,z,t)。
3. 将四维空间坐标(x,y,z,t)做投影变换,得到投影在三维空间中坐标(x,y,z)。
4. 有了三维的坐标就好办了,直接用OpenGL或者D3D绘制出来即可。
4.后记
关于四维空间,我实在没有太多的话语权。事实上,我是在看了数学记录片《dimensions》后才对它产生了兴趣。元旦节放假时,正好闲着没事做,就想着写一个四维空间的屏保来打发打发一下无聊的光棍生活,于是查了一些Wikipedia条目和相关的论文,得到一些粗浅的理解,整理出来与大家分享。如果想更深一步的学习,可以Google“高维欧氏几何学”,这是一本免费的电子书,内容相当有难度,有兴趣的同学可以挑战一下:)。
二. 六个正凸多胞体的构造
0.一些说明
首先为本文中将要帖出的代码做一些说明。我首先写了一个CObject4D基类,其中定义了三个私有纯虚函数如下:
1 private:
2 virtual void DefineVertices() = 0;
3 virtual void DefineEages() = 0;
4 virtual void DefineFaces() = 0;
下面所介绍的6个正凸多胞体都是CObject4D的子类,因此需要定义以上三个函数。此外,在CObject4D类里还定义了以下三个Protected过程:
1 protected:
2 void AddVertex(float x, float y, float z, float w);
3 void AddEdge(unsigned short v1, unsigned short v2);
4 void AddFace(unsigned short num, ...);
其中AddVertex用来添加一个顶点,参数为x,y,z,w座标(上一篇文篇中是用的x,y,z,t,但是这个t很容易让人将之同时间联系起来,其实它们之间并没有什么明显的联系,所以改成w)。AddEdge用来添加一条边,参数为组成该条边的两个顶点的序号。AddFace,当来是用来添加一条面,这是个有着可变参数的函数(如同printf),第一个参数用来指定组成该面的顶点数,后面的参数依次按顺序针方向列出组成该面的所有顶点的序号。好了,正题开始。
1.正四维单形
四维单形,英文是4-Simplex,针对正四维单形,还有一个专门的名词叫做Pentachoron。从几何学上,单形由位于n维欧氏空间上的n+1个仿射无关的点组成的点集的凸包。而正单形则更有其中每两个顶点之间的距离都相同。比如一维正单形就是一条直线,二维正单形是等边三角形,三维正单形是正四面体。四维单形有5个顶点,每两个顶点之间构成一条边,于是总共有C(5,2)=10条边(C(n,m)为二项式系数)。然后每三个顶点形成一个面,总共有C(5, 3)=10个面。构造一个正四维单形的代码如下:
1 void CSimplex::DefineVertices()
2 {
3 // 5 vertices
4 ///--------------------------------------------------------
5 // AddVertex(
6 // AddVertex(
7 // AddVertex(
8 // AddVertex(
9 // AddVertex(
10 //---------------------------------------------------------
11
12 AddVertex( 1, -1, -1,
13 AddVertex(-1, 1, -1,
14 AddVertex(-1, -1, 1,
15 AddVertex( 1, 1, 1,
16 AddVertex( 0, 0, 0,
17 }
18
19 void CSimplex::DefineEages()
20 {
21 // 10 edges
22 for (int i=0; i!=4; ++i)
23 {
24 for (int j=i+1; j!=5; ++j)
25 AddEdge(i, j);
26 }
27 }
28
29 void CSimplex::DefineFaces()
30 {
31 // 10 triangle faces
32 for (int i=0; i!=3; ++i)
33 {
34 for (int j=i+1; j!=4; ++j)
35 for (int k=j+1; k!=5; ++k)
36 AddFace(3, i, j, k);
37 }
38 }
其中,被注释的顶点集是一个“居中”的边长为2的正四维单形的5个顶点。而未被注释是图形学大牛Perlin(Perlin噪声听说过吧,得了奥斯卡奖的哦)给出的一个顶点集,边长为根号8。
2.四维超立方体
英文名为4-Hypercube,还有一个术语叫做Tesseract。立方体大家都很熟悉了,就是方方的,拥有8个顶点,12条长度相等的棱,6个全等的面的那么一个玩意儿。当然水立方并不是一个立方体而只是一个长方体,之所以叫水立方估计是因为叫水长方太难听,不够艺术。立方体可以看做是由互相平行的两个矩形面连结对应的顶点构成。同样,四维超立方体也可以看做是由互相平行的两个立方体连结对应的顶点构成,如下图(摘自Wikipedia,感谢一下):
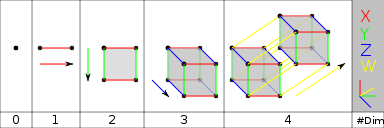
根据上图,要构造一个边长为a的四维超立方体很简单,先在t=t0的位置上构造一个普通的边长为a的立方体,再在t=t0+a的位置上再构造一个边长为a的立方体,然后将两个立方体对应的顶点连起来即可。四维超立方体一共有16个顶点,32条边,24个面,每相邻的8个顶点都构成一个立方体,总共有8个这样的立方体(根据四维空间的欧拉公式,有V+F=E+C,即顶点数加面数等于边数加上胞体数),所以四维超立方体又被称做是正8胞体。一个“标准”的四维超立方体的所有顶点是(±1, ±1, ±1, ±1)的一个全排列。由此构造出一个一个“标准”的四维超立方体的C++代码如下(因为几何结构比较清楚明了,就不详细解释了,虽然一些位运算看起来比较可疑,但也应该很好懂的吧,不好理解的话在纸上画画:))。
1 #define V(i,j) ((i&j) > 0 ?
2
3 void CTesseract::DefineVertices()
4 {
5 for (int i=0; i!=16; ++i)
6 {
7 float x = V(i, 1);
8 float y = V(i, 2);
9 float z = V(i, 4);
10 float w = V(i, 8);
11 AddVertex(x, y, z, w);
12 }
13 }
14
15 void CTesseract::DefineEages()
16 {
17 for (int i=0 ; i!=15 ; ++i)
18 for (int j=1; j!=16; j*=2)
19 {
20 if ((i & j) == 0)
21 {
22 AddEdge(i, i+j);
23 }
24 }
25 }
26
27 void CTesseract::DefineFaces()
28 {
29 for (int i=0; i!=GetNumEdges(); ++i)
30 {
31 Edge edge = GetEdge(i);
32 int v1 = edge.v1;
33 int v2 = edge.v2;
34
35 for (int j=1; j!=16; j*=2)
36 {
37 if ((v1&j)==0 && (v2-v1)<j)
38 {
39 AddFace(4, v1, v2, v2+j, v1+j);
40 }
41 }
42 }
43 }
3.正16胞体
正16胞体(16-cell)是正8面体在四维空间中的类比,英文术语为Hexadecachoron,它们都属于cross-polytope(不知道中文该怎么翻译,交叉多胞体?)家族。所谓的cross-polytope是指顶点集为(±1, 0, 0, …, 0)的全排列的几何结构,即其顶点分别对称地分布在坐标轴的两侧,如下图,从左至右分别为2维,3维和4维的cross-polytope。图片来自wikipedia。

正16胞体有8个顶点,24条边,32个面,16个正四面体胞单元。其8个顶点分别为(±1, 0, 0, 0)的排列,也就是(±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1)。每两个不相对的顶点形成一条边。每三个两两不相对的顶点构成一个三角面。构造一个正16胞体的代码如下:
1 void CHexadecachoron::DefineVertices()
2 {
3 AddVertex(-1, 0, 0, 0);
4 AddVertex( 0, -1, 0, 0);
5 AddVertex( 0, 0, -1, 0);
6 AddVertex( 0, 0, 0, -1);
7 AddVertex( 1, 0, 0, 0);
8 AddVertex( 0, 1, 0, 0);
9 AddVertex( 0, 0, 1, 0);
10 AddVertex( 0, 0, 0, 1);
11 }
12
13 void CHexadecachoron::DefineEages()
14 {
15 for(int i=0; i!=7; ++i)
16 {
17 for (int j=i+1; j!=8; ++j)
18 {
19 if ((j-i) != 4)
20 AddEdge(i, j);
21 }
22 }
23 }
24
25 void CHexadecachoron::DefineFaces()
26 {
27 for (int i=0; i!=6; ++i)
28 for (int j=i+1; j!=7; ++j)
29 for (int k=j+1; k!=8; ++k)
30 {
31 if ((j-i)!=4 && (k-i)!=4 && (k-j)!=4)
32 {
33 AddFace(3, i, j, k);
34 }
35 }
36 }
4.正24胞体
正24胞体(24-cell)的英文术语为Icositetrachoron,它是唯一没有与其相似的3维类比正多面体的正多胞体。正24胞体有24个顶点,96条边,96个三角形面,以及24个正8面体胞单元。下图是其到三维空间的一个投影。

正24胞体的24个顶点的分布很规则,像是一个4维超立方体和一个正16胞体的并集:分别是(±1, 0, 0, 0)的排列和(±0.5, ±0.5, ±0.5, ±0.5)的排列。前面8个顶点像是构成了一个正16胞体,而后面16个顶点也像是构成了一个缩小了一半的标准4维超立方体。构造这24个顶点的代码如下:
1 #define V(i,j) ((i&j) > 0 ?
2
3 void CIcositetrachoron::DefineVertices()
4 {
5 AddVertex(-1, 0, 0, 0);
6 AddVertex( 0, -1, 0, 0);
7 AddVertex( 0, 0, -1, 0);
8 AddVertex( 0, 0, 0, -1);
9 AddVertex( 1, 0, 0, 0);
10 AddVertex( 0, 1, 0, 0);
11 AddVertex( 0, 0, 1, 0);
12 AddVertex( 0, 0, 0, 1);
13
14 for (int i=0; i!=16; ++i)
15 {
16 float x = V(i, 1);
17 float y = V(i, 2);
18 float z = V(i, 4);
19 float w = V(i, 8);
20 AddVertex(x, y, z, w);
21 }
22 }
正24胞体的边的连结和面的构造稍稍有点复杂。先说说边的连结。首先,将后16个顶点按照四维超立方体的方式连结起来,这样先得到32条边。如下图:
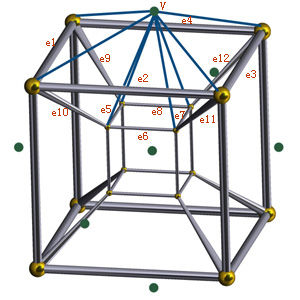
然后将前面8个顶点(上图中深绿色的顶点,注意最中间其实是有两个:(0,0,0,-1),(0,0,0,1)只是投影之后重叠了而已)分别与相邻的8个位于“超立方体”中的顶点相连。在上图中我只连了一个。在侧面的顶点分别与“大立方体”中的四个顶点和“小立方体”中的四个顶点相连。而在中间的(0,0,0,1)与“大立方体”的8个顶点相连形成8条边,(0,0,0,-1)与“小立方体”的8个顶点相连也得到8条边。这样,前面的8个顶点各形成8条边,总共64条边,加上在“四维超立方体”中的32条边,总共得到96条边。构造这96条边的代码如下:
1 void CIcositetrachoron::DefineEages()
2 {
3 for (int i=0 ; i!=15 ; ++i)
4 for (int j=1; j!=16; j*=2)
5 {
6 if ((i & j) == 0)
7 {
8 AddEdge(i+8, i+j+8);
9 }
10 }
11
12 int power[] = {1, 2, 4, 8};
13 for (/*int */ i = 0; i!=16; ++i)
14 {
15 for (int j=0; j!=4; ++j)
16 {
17 if ((i&power[j]) > 0)
18 {
19 AddEdge(i+8, j+4);
20 }
21 else
22 {
23 AddEdge(i+8, j);
24 }
25 }
26 }
27 }
然后是96个3角面。还是首先将后16个顶点构造出一个“超立方体”的框架。还是如上图。然后,前8个顶点每个分别与其相邻的12条边形成12个面,比如在上图中分别为v-e1, v-e2, v-e3….v-e12. 于是就得到了总共12*8=96个面。构造这96个面的代码如下:
1 void CIcositetrachoron::DefineFaces()
2 {
3 int power[] = {1, 2, 4, 8};
4 int index[] = {0, 1, 1, 3, 3, 2, 2, 0};
5 int positive[8], posiNum;
6 int negative[8], negaNum;
7
8 for (int i=0; i!=4; ++i)
9 {
10 posiNum = 0;
11 negaNum = 0;
12 for (int j=0; j!=16; ++j)
13 {
14 if ((j&power[i]) > 0)
15 positive[posiNum++] = j + 8;
16 else
17 negative[negaNum++] = j + 8;
18 }
19
20 for (int k=0; k!=8; k+=2)
21 {
22 // The vertex's index of triangle
23 int t1 = index[k];
24 int t2 = index[k+1];
25 int t3 = t1 + 4; // offset 4
26 int t4 = t2 + 4; // offset 4
27 int t5 = (i==3)? -8 : 8; // offset 8
28
29 AddFace(3, positive[t1], positive[t2], i+4);
30 AddFace(3, positive[t3], positive[t4], i+4);
31 AddFace(3, positive[t1], positive[t1]+t5, i+4);
32
33 AddFace(3, negative[t1], negative[t2], i);
34 AddFace(3, negative[t3], negative[t4], i);
35 AddFace(3, negative[t1], negative[t1]+8, i);
36 }
37 }
38 }
5.正120胞体
正120胞体(120-cell),又叫做Hecatonicosachoron,是正十二面体在四维空间中的类比。正120胞体有600个顶点,1200条边,720个正五边形面,以及120个正十二面体胞结构。下图是其在三维空间的一个投影:

正120胞体的顶点集如下:
(0, 0, ±2, ±2) 的所有排列,共24个
(±1, ±1, ±1, ±√5) 的所有排列,共64个
(±φ^-2, ±φ, ±φ, ±φ) 的所有排列,共64个
(±φ^-1, ±φ^-1, ±φ^-1, ±φ^2) 的所有排列,共64个
(0, ±φ^-2, ±1, ±φ^2) 的所有偶排列,共96个
(0, ±φ^-1, ±φ, ±√5) 的所有偶排列,共96个
(±φ^-1, ±1, ±φ, ±2) 的所有偶排列,共192个
其中φ为黄金分割率,值为(1+√5)/2。^表示是乘方运算。
另,所谓的偶排列是指逆序对数为偶数的排列,数量为全排列数量的一半。
由此可见程序化构造正120胞体还是比较麻烦的。关于排列,偶排列,元组(所有正负号情况)和组合的遍历可以在《TAOCP》的第四卷中找到答案,这里直接提供一份现成的头文件,在这个头文件里,申明了vertices, edges和faces数组,直接读取即可。
下载头文件:120cell.h
6.正600胞体
正600胞体(600-cell),英文又叫Hexacosichoron,是正二十面体在四维空间中的类比。正600胞体有120个顶点,720条边,1200个三角形面,以及600个正四面体胞结构,是最漂亮的正多胞体(个人观点),如下图:

正600胞体的顶点集如下:
(±½,±½,±½,±½) 的所有排列,共16个
(0,0,0,±1) 的所有排列,共8个
½(±1,±φ,±1/φ,0) 的所有排列,共96个
这里同样提供了一个包含了正600胞体顶点、边、面信息的头文件。
下载头文件:600cell.h




 浙公网安备 33010602011771号
浙公网安备 33010602011771号