浅析Mandelbrot集合及其图形的绘制

引言

在《Foundations of F#》的第七章中，作者在介绍Math命名空间时举的例子是绘制Mandelbrot集合。这个看起来挺奇怪的东东以前还真没见过，网上一查才知道，原来它是如此的优美动人。由于该集合的定义与分形相关，所以先来了解下分形的概念。

什么是分形（Fractal）

1967年，美国数学家Mandelbrot曾出这样一个著名的问题：英格兰的海岸线到底有多长？这个问题在数学上可以理解为：用折线段拟合任意不规则的连续曲线是否一定有效？这个问题的提出实际上是对以欧氏几何为核心的传统几何的挑战。

1975年，Mandelbrot在其《自然界中的分形几何》一书中引入了分形（fractal）这一概念。从字面意义上讲， fractal是碎块、碎片的意思，然而这并不能概括Mandelbrot的分形概念，尽管目前还没有一个让各方都满意的分形定义，但在数学上大家都认为分形有以下几个特点：

1. 具有无限精细的结构；
2. 比例自相似性；
3. 一般它的分数维大子它的拓扑维数；
4. 可以由非常简单的方法定义，并由递归、迭代产生。

据说，南非海岸线的维数是1.02，英国西岸的维数是1.25。

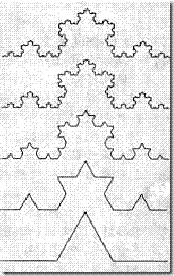
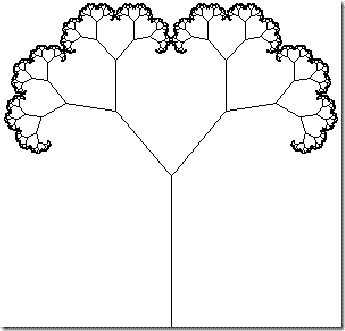
下面的两幅图有助于我们理解它的概念：

需要注意的是，分形往往由递归、迭代产生，但是我们在纸上做出的图只能作有限次的递归、迭代。

分形几何学已在自然界与物理学中得到了应用。如在显微镜下观察落入溶液中的一粒花粉，会看见它不间断地作无规则运动（布朗运动），这是花粉在大量液体分子的无规则碰撞（每秒钟多达十亿亿次）下表现的平均行为。布朗粒子的轨迹，由各种尺寸的折线连成。只要有足够的分辨率，就可以发现原以为是直线段的部分，其实由大量更小尺度的折线连成。

什么是Mandelbrot集合？

Mandelbrot集合是在复平面上组成分形的点的集合，它正是以数学家Mandelbrot命名。

Mandelbrot集合可以用复二次多项式

来定义

其中c是一个复参数。对于每一个c，从开始对f_c(z)进行迭代。

序列 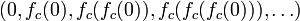的元素的模（复数具有模的概念）或者延伸到无穷大，或者只停留在有限半径的圆盘内。Mandelbrot集合就是使以上序列不延伸至无限大的所有c点的集合。

从数学上来讲，Mandelbrot集合是一个复数的集合。一个给定的复数c或者属于Mandelbrot集合M，或者不属于。比如，取c = 1，那么这个序列就是(0, 1, 2, 5, 26, ...)，显然它的值会趋于无穷大；而如果取c = i，那么序列就是(0, i, -1+i, -i, -1+i, -i,...)，它的值会一直停留在有限半径的圆盘内。

事实上，一个点属于Mandelbrot集合当且仅当它对应的序列（由上面的二项式定义）中的任何元素的模都不大于2。这里的2就是上面提到的“有限半径”。

在计算机上绘制Mandelbrot集合

计算机的屏幕上的像素只有有限个，而Mandelbrot集合中的点则有无限个。

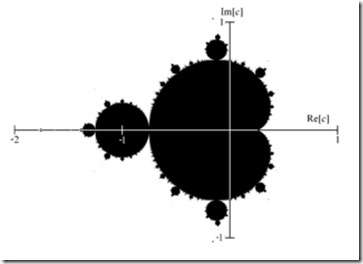
观察上面复平面的局部，Mandelbrot集合即黑色区域，实部从-2到1，虚部从-1到1，那么将两个点(-2, 1)和(1, -1)作为一个矩形的左上角顶点和右下角顶点，那么这个矩形就包含了整个Mandelbrot集合，该矩形的长为3，宽为2。我们可以将这个矩形与屏幕上的区域进行映射，也就是将屏幕上的一个像素映射为该矩形内的一点，如果该点属于Mandelbrot集合，就将该像素着为黑色，这样逐一对每个像素进行判断和着色，就可以模拟绘制Mandelbrot集合了。该矩形的长宽比为3：2，我们在屏幕上可以取600 * 400的矩形区域。

完成映射后来考虑如何判断一个点是否属于该集合。其根据就是上面的结论“一个点属于Mandelbrot集合当且仅当它对应的序列（由上面的二项式定义）中的任何元素的模都不大于2”，由于序列的的元素有无穷多个，我们只能取有限的迭代次数来模拟了，比如取100或1000次。

我们用Microsoft.FSharp.Math.Notation.complex类型来表示一个复数，它的Magnitude属性表示复数的模，我们可以通过一定次数（比如100次）的迭代，来看看前100项是不是都满足条件，如果满足就认为这个复数在Mandelbrot集合内。下面是完整的程序。

#light
open System
open System.Drawing
open System.Windows.Forms
open Microsoft.FSharp.Math
open Microsoft.FSharp.Math.Notation

// 迭代次数
let maxIterations = 100

// 映射比例
let scalingFactor = 1.0 / 200.0
// 将像素映射为复数
let mapPlane(x, y) =
    let fx = ((float x) * scalingFactor) - 2.0
    let fy = ((float y) * scalingFactor) - 1.0
    complex fx fy

let mutable iteration = 0
let mutable current = complex 0.0 0.0
let mutable temp = complex 0.0 0.0

let form =
    let image = new Bitmap(600, 400)
    for x = 0 to image.Width - 1 do
        for y = 0 to image.Height - 1 do
            iteration <- 0
            current <- mapPlane(x, y)
            temp <- current
            // 判断当前点是否在Mandelbrot集合内
            while(temp.Magnitude <= 2.0 && iteration < maxIterations) do
                temp <- temp * temp + current
                iteration <- iteration + 1
            
            // 如果在，像素为黑色    
            if iteration = maxIterations then
                image.SetPixel(x, y, Color.Black)
            else
                image.SetPixel(x, y, Color.White)
               
    let temp = new Form() in
    temp.Paint.Add(fun e -> e.Graphics.DrawImage(image, 0, 0))
    temp.Height <- 435
    temp.Width <- 600
    temp.Text <- "Draw Mandelbrot Set"
    temp
   
[<STAThread>]
do Application.Run(form)

下面是效果图

这张图是黑白的，我们可以把它变成彩色的。看这一部分代码：

// 如果在，像素为黑色    
if iteration = maxIterations then
    image.SetPixel(x, y, Color.Black)
else
    image.SetPixel(x, y, Color.White)

只有iteration等于maxIterations，当前的复数才属于Mandelbrot集合，这时将像素着为黑色；如果不在集合内，我们可以想办法着为彩色。考虑红橙黄绿蓝靛紫七种颜色，把它们存储在数组中，然后根据iteration的值来取相应的颜色：

// 七种颜色
let colors = [| Color.Red; Color.Orange; Color.Yellow; 
                Color.Green; Color.Blue; Color.Indigo; 
                Color.Purple; |]

// 如果在，像素为黑色    
if iteration = maxIterations then
    image.SetPixel(x, y, Color.Black)
else
    image.SetPixel(x, y, colors.[iteration % colors.Length])

完整的代码是：

#light
open System
open System.Drawing
open System.Windows.Forms
open Microsoft.FSharp.Math
open Microsoft.FSharp.Math.Notation

// 迭代次数
let maxIterations = 30

// 七种颜色
let colors = [| Color.Red; Color.Orange; Color.Yellow; 
                Color.Green; Color.Blue; Color.Indigo; 
                Color.Purple; |]

// 映射比例
let scalingFactor = 1.0 / 200.0
// 将像素映射为坐标
let mapPlane(x, y) =
    let fx = ((float x) * scalingFactor) - 2.0
    let fy = ((float y) * scalingFactor) - 1.0
    complex fx fy

let mutable iteration = 0
let mutable current = complex 0.0 0.0
let mutable temp = complex 0.0 0.0

let form =
    let image = new Bitmap(600, 400)
    for x = 0 to image.Width - 1 do
        for y = 0 to image.Height - 1 do
            iteration <- 0
            current <- mapPlane(x, y)
            temp <- current
            // 判断当前点是否在Mandelbrot集合内
            while(temp.Magnitude <= 2.0 && iteration < maxIterations) do
                temp <- temp * temp + current
                iteration <- iteration + 1
            
            // 如果在，像素为黑色    
            if iteration = maxIterations then
                image.SetPixel(x, y, Color.Black)
            else
                image.SetPixel(x, y, colors.[iteration % colors.Length])
               
    let temp = new Form() in
    temp.Paint.Add(fun e -> e.Graphics.DrawImage(image, 0, 0))
    temp.Height <- 435
    temp.Width <- 600
    temp.Text <- "Drawing Mandelbrot Set"
    temp
   
[<STAThread>]
do Application.Run(form)

下面是效果图

当然这只是着彩色方式的一种，如果你有兴趣，可以查看后面给出的参考文章。

小结

Mandelbrot集合的图形表示可以让我们认识到纯粹的数学之美，与之相关的分形几何学则是无处不在的，不得不感叹数学的力量。由于分形几何学知识的匮乏，本文只能给出Mandelbrot集合的定义，并以最容易理解的方式绘制出该集合。这里使用的语言是F#，而不是C#，以后会尽量作出一些采用F#的更为实用的例子。

参考：

《Foundations of F#》 by Robert Pickering
神奇的分形艺术
Mandelbrot_Set_Wikipedia
分形是什么？