SciTech-EECS-计算机图形学(一): 向量及其运算和运用：加减法、点积(乘)、叉积(乘)

SciTech-EECS-计算机图形学(一):

向量及其运算和运用：加减法、点积(乘)、叉积(乘)

https://blog.csdn.net/qw8704149/article/details/116543685

向量、向量加减法、向量的点积（乘）、向量的叉积（乘）

1. 向量
2. 向量的矩阵表示
   3 向量加法
   3.1 三角形定则
   3.2 平行四边形定则
   4 向量减法
   5 向量的点积（乘）
   5.1 点积介绍
   5.2 向量点乘矩阵表示法
   5.3 向量点乘适用的运算定律
   5.4 一个向量投影到另一个向量
   5.5 向量点乘的应用
   5.5.1 计算两个向量的夹角
   5.5.2 判断两个向量的方向
   5.5.3 判断两个向量是否接近
   6 向量的叉积（乘）
   6.1 叉积（乘）介绍
   6.2 向量叉乘矩阵表示法
   6.3 向量叉乘适用的运算定律
   6.4 向量叉乘的应用
   6.4.1 判断一个向量在另一个的左侧还是右侧
   6.4.2 判断一个点是否在三角形内部

1. 向量

• 向量 定义
  指的是既有 Magnitude，又有 Direction 的量。物理学上也称为矢量。
• 向量有平移不变性。
  注意，向量在空间中没有具体的位置。
  即: 向量只与大小和方向有关系，和向量的起点和终点没有关系。
  向量也只包含两个属性：大小和方向。
• 向量的表示 与 计算方法:
  • 几何表示:
    由 A 点指向 B 点的一个有向线段，称为向量 a
  • 符号表示:
    通常使用 "小写字母上面加上向右的箭头 → "表示，例如\(\large \vec{a}\)；
    或者使用粗体的小写字母表示，例如 a。
  • 数学表示 及 计算方法:
    数学表示: 对空间的两个点 𝐴 和 𝐵，从 𝐴 到 𝐵 的向量可以表示为 \(\large \vec{𝐴𝐵}\)，
    计算方法: \(\large \vec{𝐴𝐵}\) = 𝐵 − 𝐴。
    

• a =\(\large \vec{a}\)= B - A，
  用有向线段的结束点B的坐标，减去起始点A的坐标，就得到这个向量 a的坐标表示.
• |a|，表示向量a的长度
• â， 表示单位向量，有 â = a / |a|

2. 向量的矩阵表示

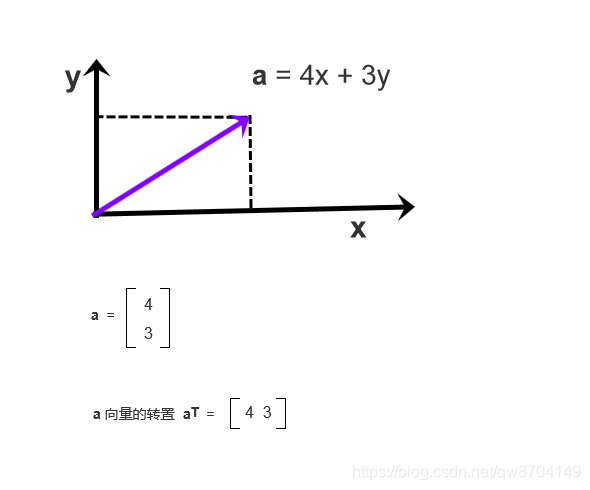
如图，向量 a 在X轴和Y轴的分量分别为4和3，
那么可以用这两个分量以矩阵的形式表示这个向量,
上图中纵向排列的被称为列向量，转置后被称为行向量，它们都表示同一个向量。

3 向量加法

向量加法不同于普通数学加法，它还具有方向属性，
因此向量加法采用三角形定则或平行四边形定则计算

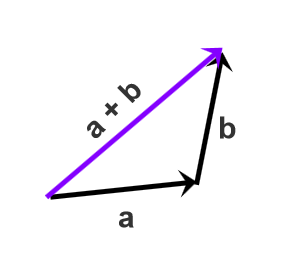
• 3.1 三角形定则
  将各个向量依次首尾顺次相接，结果为第一个向量的起点指向最后一个向量的终点。
  向量a 加 向量b，将a和b 首尾相连后，由a的起点指向b的终点，就是 a + b
  
• 3.2 平行四边形定则
  将两个向量平移至公共起点，以这两个向量绘制平行四边形，从公共起点到公共终点的向量为结果向量
  将向量a和向量b的起点移到左下角的公共起点，然后以这两个向量绘制平行四边形，
  由公共起点指向公共终点就是 a + b
• 4 向量减法
  向量减法一般使用三角形定则运算
  在这里插入图片描述
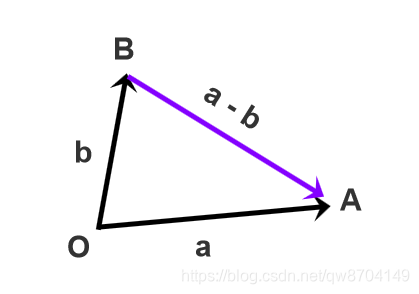
  将两个向量平移至公共起点O，从减数向量的终点B指向被减向量的终点A为相减结果
  将向量a和向量b的起点移到左下角的公共起点O，从点B指向点A的向量就是 a - b
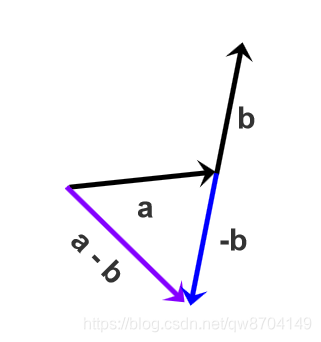
  向量相减也可以当做加上一个负的向量，负向量代表大小相等方向相反的向量
  在这里插入图片描述
  将向量相减当做加上一个负的向量，即 a - b = a + (-b)

向量的点积(内积)和叉积(外积)：

• 点积结果是一个标量，表示 两个向量 在某一轴上的投影的乘积；

• 叉积结果是一个新的向量，其方向垂直于两个原向量，且满足右手定则。

• 重要的特殊的点积：
  一个向量和自己点积，结果就是向量长度的平方，即 向量长度就等于与自身点积的平方根。
  在二维平面中，一个二维向量可以用一个箭头来表示，这个箭头起始于原点，终点坐标。
  三维向量和二维向量类似，可以表示为三维平面中的一个箭头，只不过坐标变成了三维。
  如果两个的向量的点积为零，说明这两个向量是垂直的，它们之间的角度为90ᵒ。
  我们可以直观地看到这种情况，当这两个向量分别为单位向量。
  而当两个向量之间的角度等于。当两个向量之间的角度大于。
  分别为向量中的两个元素，而。当两个向量之间的角度小于。

• 5 向量的点积（乘）
  5.1 点积介绍
  在这里插入图片描述
  两个向量的点积（乘），记作 a · b

两个向量的点积等于两个向量的长度相乘再乘以两个向量夹角的余弦值

a · b = |a| |b| cosθ

两个向量夹角的余弦值等于两个向量的点积除以两个向量的长度的积

在这里插入图片描述

两个向量夹角的余弦值也等于两个向量的单位向量的点乘

在这里插入图片描述

5.2 向量点乘矩阵表示法
二维向量点乘矩阵表示法
在这里插入图片描述
三维向量点乘矩阵表示法
在这里插入图片描述

5.3 向量点乘适用的运算定律
交换律 a · b = b · a
分配律 a · (b + c) = a · b + a · c
结合律 (ka) · b = a · (kb) = k(a · b)

5.4 一个向量投影到另一个向量
在这里插入图片描述

向量 b⊥ 为向量 b 在向量 a 上的投影向量
向量 b⊥ 与向量 a 方向相同，若向量 a 是单位向量则有，

在这里插入图片描述

通过三角函数的性质，可以得出

|b⊥| = |b|cosθ

5.5 向量点乘的应用
5.5.1 计算两个向量的夹角
在这里插入图片描述
已知两个向量，可以通过以上公式求出cosθ， 然后通过反余弦函数计算出夹角θ

5.5.2 判断两个向量的方向
在这里插入图片描述

先将向量a和向量b做归一化处理
在这里插入图片描述
上述公式可变换为 a · b = cosθ

如果 a · b 等于1，说明夹角是0度或360度，两个向量重合
如果 a · b 大于0小于1，说明夹角在0度到90度之间或270度与360度之间，即向量 a 与向量 b 是相同的方向
如果 a · b 等于0，说明夹角是90度或270度，两个向量垂直
如果 a · b 小于0大于-1，说明夹角在90度到270度之间 (不包括180度)，即向量 a 与向量 b 方向相反
如果 a · b 等于-1，说明夹角是180度，两个向量方向相反，如上图中向量 a 与向量 b2

5.5.3 判断两个向量是否接近
判断两个向量是否接近，其实是判断方向的更近一步的应用，上面提到如果两个向量点乘等于1说明两个向量重合，那么两个向量点乘越接近1说明两个向量越接近，这个性质在光反射模型中计算高光时非常有用，先简单说一下，在近似镜面反射中，如果反射光的方向与人眼观察方向很接近，那么在一定的范围内可以观察到物体表面的高光

6 向量的叉积（乘）
6.1 叉积（乘）介绍
两个向量的叉积（乘）的结果是一个向量，记作c = a x b
在这里插入图片描述
向量叉乘结果方向确定
使用右手螺旋法则确定向量 c 的方向，首先做出点赞手势，四指方向从向量 a 旋转到向量 b，这时拇指方向就是向量 c 的方向

向量叉乘的一些性质

向量 a 叉乘向量 b 的结果为向量 c
向量 c 垂直于向量 a， 向量 c 垂直于向量 b，继而向量 c 垂直于向量 a与向量 b组成的平面

向量 a 叉乘向量 b 等于负的向量 b 叉乘向量 a
a x b = -b x a

两个向量的叉乘的模长等于两个向量的模长相乘再乘以两个向量夹角的正弦值
|a x b| = |a| |b| sinΦ

两个向量平行，因为sin0 = 0，则得到 |a x b| = 0 ，0 代表0向量
|a x b| 的值是以向量 a 和向量 b 为边组成的平行四边形的面积

6.2 向量叉乘矩阵表示法
向量的叉乘可以写成一个向量对应的矩阵乘以另一个向量
在这里插入图片描述
通过矩阵乘法规则推理得出下面结果
在这里插入图片描述

6.3 向量叉乘适用的运算定律
分配律 a x (b + c) = a x b + a x c
结合律 a x (kb) = k(a x b)

6.4 向量叉乘的应用
6.4.1 判断一个向量在另一个的左侧还是右侧
根据右手螺旋定则，如果向量 a 叉乘向量 b 的结果 > 0，右手旋转时时从 a 向量转向 b 向量，所以 b 向量在 a 向量的左侧，若叉乘结果< 0,则 b 向量在 a 向量的右侧

向量 a 叉乘向量 b > 0, b 向量在 a 向量的左侧
向量 a 叉乘向量 b < 0, b 向量在 a 向量的右侧

6.4.2 判断一个点是否在三角形内部
在这里插入图片描述
判断一个点是否在三角形内部的步骤

把三角形的三条边按一定的顺序依次连接，组成三个向量，上图中是按逆时针方向连接
取其中的一个向量AB，构造一个向量AP，从向量的起点A指向P点，向量AB叉乘向量AP，结果 > 0，所以 AP 在 AB 的左侧
取下一个向量BC，计算向量BC叉乘向量BP，结果 > 0， 得到BP 也在 BC 的左侧
取下一个向量CA，计算向量CA叉乘向量CP，结果 > 0， 得到CP 也在 CA 的左侧
由第2,3,4步的结果推断出P点在三角形内部，如果第2,3,4步中有一个结果有一个不在左侧则P点不在三角形内部
如果开始连接三角形时按逆时针方向连接，即三条边的向量为AC，CB，BA，则第2,3,4步叉乘的结果都<0,说明P点与三条边的向量起点组成的向量均在对应边向量的一侧，也可以判断P点在三角形内部，实际上判断点是否在三角形内部的依据是，边向量的起点与要判断的点组成的向量是否在三个边向量的同一侧

向量运算
提到 向量运算，首先就是 点乘 和 叉乘。 点乘（Dot Product）： 也叫向量的内积、数量积，公式描述为： 向量a·向量b = |a||b| cosθ = a1·b1 + a2·b2 点乘 的几何意义是一个向量在另外一个向量上的投影。 叉乘（Cross Produ

点积与向量积(点乘与叉乘)
cross(V1, V2) = |V1| |V2| sin<V1, V2> * n (n指右手定则确定出的单位向量) = (x1y2 - y1x2) * k (k为z轴单位向量(0,0,1)) = (0, 0, x1y2-y1x2) 矩阵表示为:i-X轴单位向量 j-Y轴单位向量 k-Z轴单位向量 i * j = k j * i = -K (i, j, k) = (y10-0y...

向量运算在图形与图像处理中的应用
本文深入探讨了向量在三维图形和图像处理领域的基础作用,重点介绍了向量数量积和向量积的概念及其应用。
通过具体实例,如计算三角形和多边形面积,展示了向量积在几何计算中的优势。
此外,文章还阐述了如何使用向量积法高效求解任意多边形面积,避免了传统方法在精度和计算量上的局限。

向量运算精要
V对于乘法运算封闭。 向量空间中存在一个元素0,对于V的任意元素P都有 P+0 = 0+p = P 向量中的任意元素P,都有一个元素Q 使得Q+P=0 参考: 点积、叉积:http://blog.csdn.net/dcrmg/article/details/52416832 向量投影:http://www.cnblogs.com/graphics/archive/2010/08/03/1791626.html...
继续访问

向量的点乘、叉乘在Unity中的应用区别与原理_unity 点乘和叉乘的区别...
本文详细介绍了向量的点乘和叉乘运算。点乘用于计算两个向量之间的角度,其结果为标量;叉乘则用于确定两个向量构成平面的垂直向量,结果为向量。文章还解释了如何在Unity3D中使用这两种运算。 摘要生成于C知道,由

向量积的定义与运算
定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b(这里“×”并不是乘号,只是一种表示方法,与“·”不同,也可记做“∧”)若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系。若a、b平行,则a×b=0,a...

首先如果两个二维向量不共线，那么它们两个做线性变化（缩放）可以表示出这个平面内的所有向量：
而在空间中，两个不共线向量的所有线性组合，可以描绘出一个平面：
但是如果第三个向量落在前两个向量所组成的平面上：

判断多边形的凹凸性和计算多边形面积:利用向量叉乘_向量叉乘正负值-CSD...
(2)关于向量叉乘的坐标运算: 如果是在二维直角坐标的时候,相当于u3=0,v3=0 也就是 所以关于叉乘最后的结果,如果是正的,说明对应的三角形面积为“正”,也就是对应的为凸的。如果为“负”,也就是为凹的。 (3)叉乘的正负和多边形的凹凸性关系 把多边形找出固定一个点为P1,然后按给的点顺序设为P2和P3。也...

向量加法图像向量的加法口诀：首尾相连，首连尾，方向指向末向量。
向量的减法图像向量的减法口诀：首首相连，尾连尾，方向指向被减向量。
以第一个向量的终点为起点，以第二个向量的终点为终点的向量是两向量的

MATLAB 提供了多种向量运算，例如向量与数的四则运算、向量与向量之间的加减运算、点积、叉积和混合积等。