Bayesian Optimization 贝叶斯优化

Bayesian Optimization 贝叶斯优化

贝叶斯优化是一种基于概率模型的优化方法，特别适合高成本实验（如生物化学实验）。

我做的一个ai4s项目需要用到这个，简单记录一下。

Introduction

什么时候需要Bayesian Optimization？

在定义域内最大化 \(f(x)\)，而观测 \(f(x)\)比较昂贵

\(f(x)\)是一个黑盒的，没有导数

模拟退火 就是一个黑盒优化模型

Gaussian process （GP）

不停更新一个多维的高斯分布

我们考虑 \(d\) 维变量 \(x\)（维度通常不高于20）

有k个 \(x_{1:k}\) 可以考虑高斯分布：

​ \(f(x_{1:k})\)~\(N(\mu_0(x_{1:k}),\Sigma_0(x_{1:k}))\)

其中 \(\mu_0(x_{1:k})\) 是1*k矩阵

而 \(\Sigma_0(x_{1:k})\) 是k*k矩阵

预测一个置信区间

对比岭回归和高斯过程

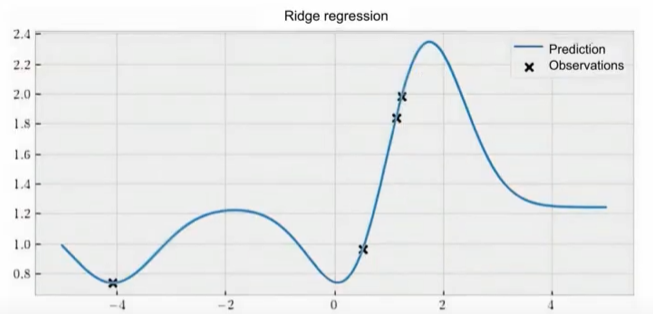
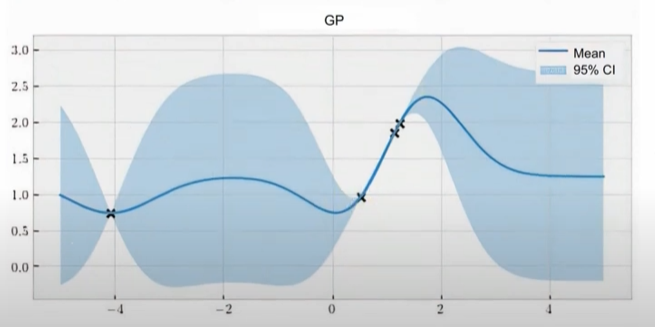
GP中给出95%置信区间，深蓝色的线是均值。浅蓝越宽，不确定性越强。

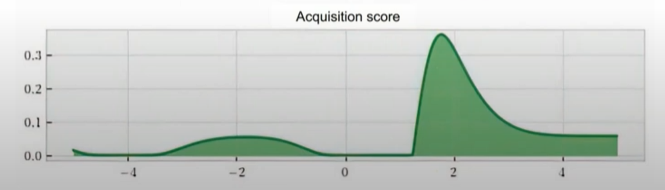
绿色的表对应的是各个值出现更好y值的可能性，为0的地方就说明已经可以确定了，没必要采样

也就说图中1.8左右的位置就是下一个采样点 ，\(f(1.8)\)可能是一个不错的值

然后我们重复上面几步就能得到一个不错的结果，比随机取点强不少

过程很神奇，反正就是能猜对极值点。能猜对的原因是有一些先验的知识。

Summary

适用的Scenario：资源有限，\(f(x)\) 比较贵，有一些先验信息。

如果采样成本低，我们就没有理由费这事了

Reference

参考文献：Bayesian Optimization in Action（Quan Nguyen）

参考视频：BV1wC4y1Q7pa，BV1h8411T7eQ