AT AGC005 题解
A
栈维护括号匹配，\(S \to (, T \to )\)。
#include <bits/stdc++.h>
using i64 = long long;
void solve() {
std::string s;
std::cin >> s;
std::stack<char> stc;
for (auto i : s) {
if (i == 'T' && stc.size()) {
if (stc.top() == 'S') {
stc.pop();
continue;
}
}
stc.push(i);
}
std::cout << stc.size() << "\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
solve();
return 0;
}
B
一开始看错题了，注意题目表达的是“所有子区间最小值之和”，考虑平衡树。将所有元素按照 \((a_i, i)\) 绑入，按照 \(a_i\) 的大小排序之后按次插入平衡树中，每次去找当前位置的前驱后继就可以了，统计答案是简单的乘法原理。
#include <bits/stdc++.h>
#include <bits/extc++.h>
using i64 = long long;
constexpr int N = 2e5 + 7;
int n;
i64 ans;
struct Elem {
int v, i;
bool operator < (const Elem &rhs) const {
return v < rhs.v;
}
};
int a[N];
std::vector<Elem> vec;
__gnu_pbds::tree<int, __gnu_pbds::null_type, std::less<int>, __gnu_pbds::rb_tree_tag, __gnu_pbds::tree_order_statistics_node_update> tr;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
vec.push_back({a[i], i});
}
std::sort(vec.begin(), vec.end());
tr.insert(0); tr.insert(n + 1);
for (const auto &[v, i] : vec) {
int l = i - *tr.upper_bound(i), r = *std::prev(tr.lower_bound(i)) - i;
ans += 1ll * v * l * r;
tr.insert(i);
}
std::cout << ans << "\n";
return 0;
}
C
究极无敌简单题。考虑树上最远距离就是直径，找到距离最远的两个点抓出来做匹配，容易发现其实就是走到中点前降、走过中点之后升的这么一个过程，开桶每次匹配两个上去，如果匹配不上报告无解。
#include <bits/stdc++.h>
using i64 = long long;
constexpr int N = 107;
int n, mxd;
int a[N], cnt[N];
int work() {
int mid = mxd / 2 + 1;
for (int i = mid; i <= mxd; i++) {
cnt[i] -= 2;
if (cnt[i] < 0)
return 0;
}
if (!(mxd & 1)) {
cnt[mid - 1]--;
if (cnt[mid - 1] < 0)
return 0;
mid--;
}
for (int i = 1; i <= mid; i++) {
if (cnt[i])
return 0;
}
return 1;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i <= n; i++) {
std::cin >> a[i];
cnt[a[i]]++;
mxd = std::max(mxd, a[i]);
}
std::cout << (work() ? "Possible" : "Impossible") << "\n";
return 0;
}
D
剽窃几张图。
组合+容斥好题。一个直观的观察是，要把这个绝对值丢到几何上的“距离”来考虑问题，但是一维上只能叉掉两个位置，考虑丢到一个矩阵上：
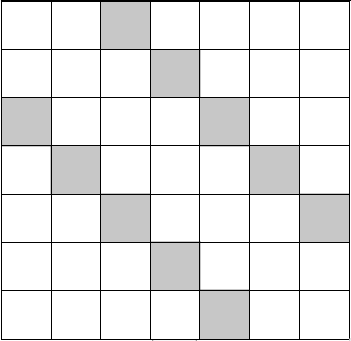
所求的排列数就是在这样一个 \(n \times n\) 的方格中放置 \(n\) 个不能互相攻击的车，且在阴影格子上不能放的方案数。
对这个东西进行容斥求解，令 \(f(i)\) 表示无视阴影并在其中放置 \(i\) 个车，剩下随便摆的方案数，则由容斥原理有答案为 \(\sum_{i = 0}^{n} (-1)^i f(i) \times (n - i)!\)。考虑怎么求解 \(f(i)\)，注意到阴影不能放，同一行同一列上的阴影也不能同时放（钦定之外随便放可能放到阴影里），连边同行或同列的阴影格子，有 \(f(i)\) 为矩阵图的最大独立集（最大的点集使得点集中任意两点都没有边直接相连）：
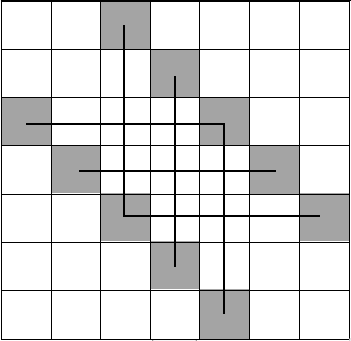
注意到这张图由若干条不相交的链构成，我们把链连接起来 DP 计数：求从链上节点选取 \(i\) 个节点，其中相邻的链头链尾可以相邻，其他位置不能相邻的方案数。
有 \(O(n^2)\) 的做法，具体地，将 \(2n\) 个点按链的顺序排成一行，令 \(g(i, j)\) 表示考虑前 \(i\) 个点，选出 \(j\) 条互不相邻的边的方案数，同时维护一个 \(h(i)\) 表示第 \(i\) 个点是否为链头能和上一个点相邻。转移为：
\[g(i, j) = g(i - 1, j) + ([j \gt 0] \times [h(i - 1) \neq 1] \times g(i - 2, j - 1))
\]
前者 \(g(i - 1, j)\) 表示不选择 \((i - 1, i)\)，直接继承 \(f(i - 1, j)\)；后者表示选边 \((i - 1, i)\)，其中要求 \(i - 1\) 不是链头且有边可选，选了这条边之后 \(i - 1, i\) 都被使用，状态跳回继承 \(i - 2\) 的状态增加 \(g(i - 2, j - 1)\)。
#include <bits/stdc++.h>
using i64 = long long;
constexpr int N = 2e3 + 7;
constexpr int P = 924844033;
int n, m, ans;
int dp[N * 2][N];
int t, fac[N], a[N * 2];
void init() {
fac[0] = 1;
for (int i = 1; i <= n; i++) {
fac[i] = 1ll * fac[i - 1] * i % P;
}
a[t] = 1;
for (int i = 1; i <= (n - m) % m; i++) {
t = t + (n - m) / m + 1;
a[t] = 1;
t = t + (n - m) / m + 1;
a[t] = 1;
}
for (int i = 1; i <= m - (n - m) % m; i++) {
t = t + (n - m) / m;
a[t] = 1;
t = t + (n - m) / m;
a[t] = 1;
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> m;
init();
dp[0][0] = 1;
for (int i = 1; i <= t; i++) {
for (int j = 0; j <= n; j++)
dp[i][j] = (dp[i - 1][j] + (j ? dp[i - 1 - (!a[i - 1])][j - 1] : 0)) % P;
}
for (int j = 0; j <= n; j++) {
ans = (ans + 1ll * dp[t][j] * fac[n - j] % P * (j & 1 ? P - 1 : 1)) % P;
}
std::cout << ans << "\n";
return 0;
}
E
直观题，从样例四那个无解情况入手，一个追击一个逃亡，作为先手，要么重复在某两个点跳跃、要么一直逃跑让后手的追不到，满足前一个条件是追你的人从一端赶到另一端至少要走三条边，此时就达成了反复横跳的条件。对于后手，肯定是找最近的路去跟，所以两个人走的都是一条链。
#include <bits/stdc++.h>
using i64 = long long;
constexpr int N = 2e5 + 7;
int n, s, t, ans;
int fa[N], dep[N], vis[N];
std::vector<int> g[N];
std::vector<int> adj[2][N];
void dfs(int u, int from, int d) {
dep[u] = d; fa[u] = from;
for (auto v : adj[1][u]) {
if (v == from)
continue;
dfs(v, u, d + 1);
}
}
void solve(int u, int from, int d) {
ans = std::max(ans, dep[u] * 2);
for (auto v : adj[0][u]) {
g[u].push_back(v);
if (v == from)
continue;
if (dep[v] == d)
ans = std::max(ans, d * 2 + 1);
else if (std::abs(dep[v] - d) == 1)
ans = std::max(ans, d * 2 + 2);
else
solve(v, u, d + 1);
}
}
bool check(int u, int v) {
if (fa[u] == v)
return 0;
if (fa[v] == u)
return 0;
if (fa[fa[u]] == v)
return 0;
if (fa[u] && fa[u] == fa[v])
return 0;
if (fa[fa[v]] == u)
return 0;
return 1;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n >> s >> t;
for (int i = 1, x, y; i < n; i++) {
std::cin >> x >> y;
adj[0][x].push_back(y);
adj[0][y].push_back(x);
}
for (int i = 1, x, y; i < n; i++) {
std::cin >> x >> y;
adj[1][x].push_back(y);
adj[1][y].push_back(x);
}
dfs(t, 0, 0);
solve(s, 0, 0);
for (int i = 1; i <= n; i++) {
for (auto j : g[i]) {
if (check(i, j)) {
std::cout << "-1\n";
exit(0);
}
}
}
std::cout << ans << "\n";
return 0;
}
F
正难则反，直接做是指数级的，反向考虑每个点对 \(k\) 下答案的贡献。大小为 \(k\) 的点集一共有 \(\binom{n}{k}\) 个，能使得一个点 \(i\) 不对 \(k\) 下答案点集产生贡献的情况当且仅当点集内所有点都在 \(i\) 的某个子树中或点集中所有点都不在以 \(i\) 为根的子树中。由此有：
\[ans_j = \sum_{i = 1}^{n} \left( \binom{n}{j} - \left( \sum_{t \in son_i} \binom{t}{j} \right) - \binom{n - siz(i)}{j} \right)
\]
同样考虑反向计算把这个 \(O(n^2)\) 级别的东西降下来，令 \(c(k)\) 表示满足 \(siz(i) = k\) 的点的数量，特别地，有 \(siz(i + n) = n - siz(i)\)，则：
\[ans_j = n \binom{n}{j} - \sum_{i = j}^{n} c(i) \times \binom{i}{j}
\]
展开 binom：
\[\begin{aligned}
ans_j &= n \binom{n}{j} - \sum_{i = j}^{n} c(i) \frac{i!}{j!(i - j)!} \\
ans_j &= n \binom{n}{j} - \frac{1}{j!} \sum_{i = j}^{n} c(i) \times \frac{i!}{(i - j)!} \\
\end{aligned}
\]
令 \(a_i = c(i) \times i!, b_i = \frac{1}{i!}\)，则有：
\[ans_j = n \binom{n}{j} - \frac{1}{j!} \sum_{i = j}^{n} a_i b_{i - j}
\]
快速计算求和符号那一块，令 \(b'_i = b_{n - i}\)，构造生成函数：
\[\begin{aligned}
A &= a_0 x^0 + a_1 x^1 + \dots + a_n x^n \\
B &= b'_i x^0 + b'_1 x^1 + \dots + b'_n x^n \\
C &= A + B
\end{aligned}
\]
则：
\[C_{j + n} = \sum_{i = j}^{n} a_i b'_{n + j - i} = \sum_{i = j}^{n} a_i b_{i - j}
\]
NTT 卷积。
#include <bits/stdc++.h>
using i64 = long long;
constexpr int N = 2e5 + 7;
constexpr int M = 5e5 + 7;
constexpr int P = 924844033;
constexpr int T = 5;
constexpr int I = 554906420;
constexpr int SZ = 1e6 + 7;
int n, lim, lg;
int fac[N], inv[N], inc[N];
int siz[N];
int a[SZ], b[SZ], r[SZ];
std::vector<int> adj[N];
template <typename T>
T expow(T a, i64 b) {
T res = 1;
for (; b; b >>= 1) {
if (b & 1) res = 1ll * res * a % P;
a = 1ll * a * a % P;
}
return res;
}
void addedge(int u, int v) {
adj[u].push_back(v);
}
void dfs(int u, int fa) {
siz[u] = 1;
for (int v : adj[u]) {
if (v == fa)
continue;
dfs(v, u);
siz[u] += siz[v];
++a[siz[v]];
}
++a[n - siz[u]];
}
int get_w(int x, int tp) {
if (~tp) return expow(T, x);
else return expow(I, x);
}
void NTT(int *A, int tp) {
for (int i = 0; i < lim; ++i) {
if (i < r[i])
std::swap(A[i], A[r[i]]);
}
for (int len = 1; len < lim; len <<= 1) {
int wn = get_w((P - 1) / (2 * len), tp);
for (int i = 0; i < lim; i += len << 1) {
int w = 1;
for (int j = 0; j < len; ++j, w = 1ll * w * wn % P) {
int x = A[i + j];
int y = 1ll * w * A[i + j + len] % P;
A[i + j] = x + y;
A[i + j + len] = x - y;
if (A[i + j] >= P) A[i + j] -= P;
if (A[i + j + len] < 0) A[i + j + len] += P;
}
}
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin >> n;
for (int i = 1; i < n; ++i) {
int u, v;
std::cin >> u >> v;
addedge(u, v);
addedge(v, u);
}
dfs(1, 0);
fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = 1ll * fac[i - 1] * i % P;
inv[1] = 1;
for (int i = 2; i <= n; ++i)
inv[i] = 1ll * inv[P % i] * (P - P / i) % P;
inc[0] = 1;
for (int i = 1; i <= n; ++i)
inc[i] = 1ll * inc[i - 1] * inv[i] % P;
a[0] = 0;
for (int i = 0; i <= n; ++i)
a[i] = 1ll * a[i] * fac[i] % P;
for (int i = 0; i <= n; ++i)
b[i] = inc[n - i];
lim = 1;
lg = 0;
while (lim <= 2 * n) {
lim <<= 1;
++lg;
}
for (int i = 1; i < lim; ++i) {
r[i] = (r[i >> 1] >> 1) | ((i & 1) << (lg - 1));
}
NTT(a, 1), NTT(b, 1);
for (int i = 0; i < lim; ++i)
a[i] = 1ll * a[i] * b[i] % P;
NTT(a, -1);
int inv_lim = expow(lim, P - 2);
for (int i = 1; i <= n; ++i) {
a[i + n] = 1ll * a[i + n] * inv_lim % P * inc[i] % P;
}
for (int i = 1; i <= n; ++i) {
a[i] = 1ll * fac[n] * inc[i] % P * inc[n - i] % P * n % P;
}
for (int i = 1; i <= n; ++i) {
a[i] -= a[i + n];
if (a[i] < 0)
a[i] += P;
}
for (int i = 1; i <= n; ++i) {
std::cout << a[i] << '\n';
}
return 0;
}
浙公网安备 33010602011771号