部分 DP 问题小记 计数、容斥原理
容斥原理
一般我们希望在 DP 中容斥掉某一个方向的限制。对于计数类 DP,我们的方程设计通常有一定特点,即对于没有容斥的部分,后面的决策包含前面决策能选到的点(此时可以根据维度信息计算答案)。对于容斥的部分,由于我们在最外层枚举钦定为 \(k\) 的 \(k\) 值,所以可以根据这个 \(k\) 转移。
容斥原理的本质是帮助我们消除一些限制条件,把真实的恰好方案数变成一些钦定方案数加加减减的结果。这样我们在实际考虑问题的时候,对于我们钦定的那些条件计数,没有钦定的条件满足或不满足都可以。
全局容斥
AT_agc036_f [AGC036F] Square Constraints
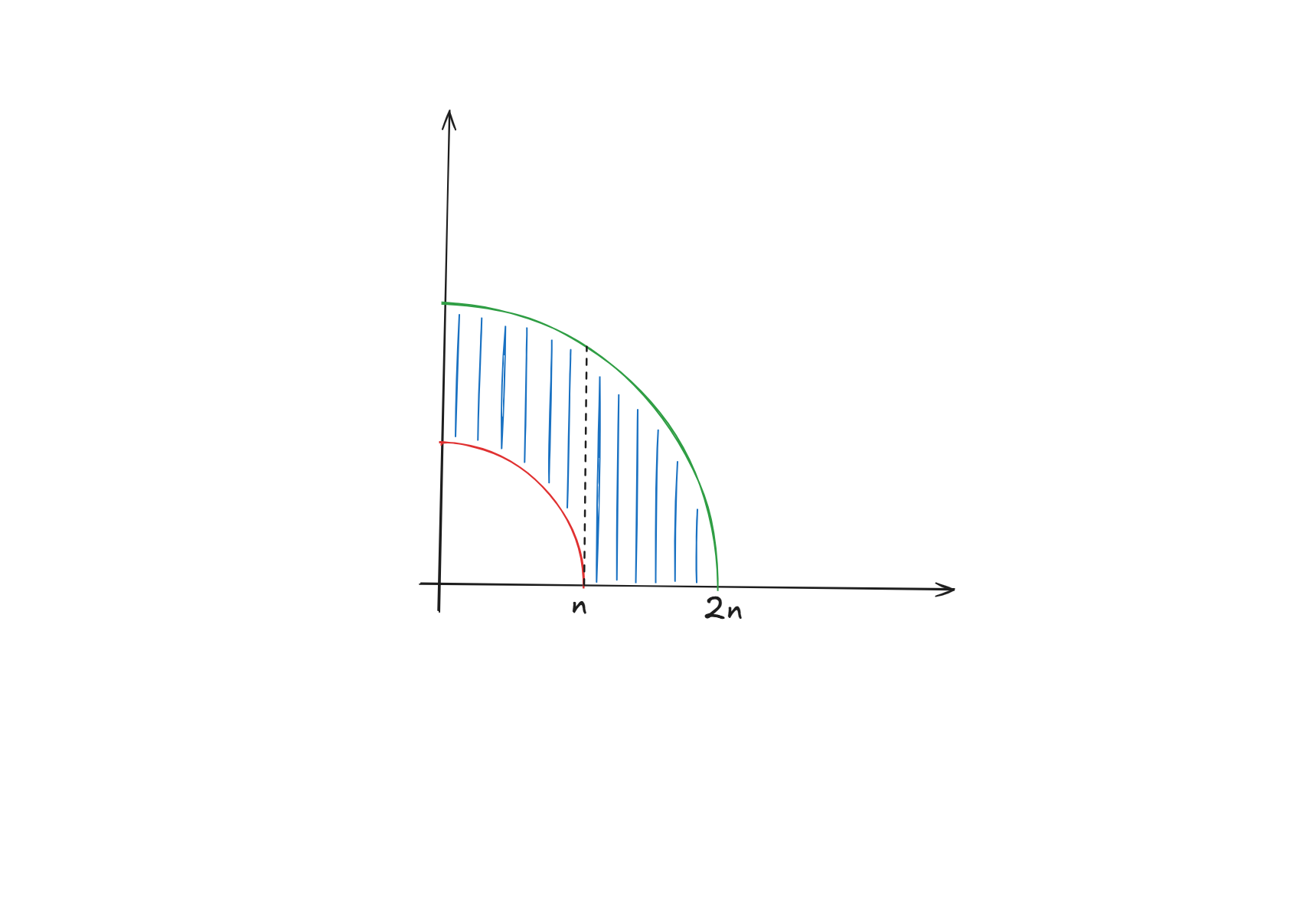
首先要把问题转化为几何直观问题。具体来说,对于每个横坐标 \(i\) 我们都希望在上图这个圆环中找到一个对应的纵坐标,且所有点纵坐标互不相同。
观察发现每个点 \(P_i\) 都有上下界,分别为 \(L_i=\lceil\sqrt{N^2-i^2}\rceil,R_i=\lfloor\sqrt{4N^2-i^2}\rfloor\)。并且对于 \([n,2n)\) 之间的点 \(L_i\) 都为 \(0\)。考虑全都没有 \(L_i\) 怎么做,显然可以 \(i\) 从大到小考虑,答案就是 \(\sum_{i=0}^{2n-1}R_i+1-(2n-i+1)\)。
考虑容斥,我们钦定 \(k\in[0,n]\) 个点取了 \(\le L_i\) 的值即非法值,我们最终的答案就是 \(\text{任意}-\text{非法}\),显然这些点只能在 \([0,n)\) 中。令 \(f_{i,j}\) 表示前 \(i\) 个点,选了 \(j\) 个 \(< L\) 的方案数,最终答案就是 \(f_{2n,k}\)。
我们在开头时说过,需要让后面决策包含前面决策。因此对于 \([n,2n)\),我们只能选 \(R\) 作为上界,取 \(R\) 为关键字。对于 \([0,n)\),容斥部分取 \(L-1\) 作为上界,因此取 \(L-1\) 作为关键字然后排序。
考虑转移后效性问题,发现选 \(L-1\) 会影响到没有下界且选 \(R\) 的点,而根据排序其数量对于 \(R\) 点可以直接统计。发现选 \(R\) 会对 \(L-1\) 产生影响,其数量也可以根据排序前缀计算。最后是有下界但是选了 \(R\) 的点。考虑它会被什么影响,显然有 \(n\) 个 \([n,2n)\) 都会影响它。重要性质:由于对于 \(n-1\) 的 \(R\) 是 \(\sqrt 2 n\) 级别的,一定比 \(n\) 大,所以所有钦定的 \(k\) 个 \(\le L\) 的也会影响到它。最后由于 \([0,n)\) 间 \(R\) 随 \(L\) 单调不减,所以无下界 \(R\) 对无下界 \(R\) 也可以实时统计。
详细转移请前往题解。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=505;
int n,pre[N];LL MOD,f[N][N],ans;
struct Lim{int L,R,id,ord;}e[N];
bool cmp(Lim x,Lim y){
if(x.L!=y.L)return x.L<y.L;
return x.R<y.R;
}
int main(){
scanf("%d%lld",&n,&MOD);
for(int i=0;i<=2*n-1;i++){
int L=0;
int R=min(int(floor(sqrt(4*n*n-i*i))),2*n-1);
if(i<n)L=int(ceil(sqrt(n*n-i*i)))-1;
else swap(L,R);
e[i+1]=Lim{L,R,i};
}
sort(e+1,e+1+2*n,cmp);
for(int i=1;i<=2*n;i++)
pre[i]=pre[i-1]+(e[i].id>=n);
for(int k=0;k<=n;k++){
f[0][0]=1;
int cnt1=0,cnt2=0;
for(int i=1;i<=2*n;i++){
for(int j=0;j<=min(k,i-pre[i]);j++){
if(e[i].id<n){
LL ch1=max(0,e[i].L+1-(j-1)-pre[i-1]);
LL ch2=max(0,e[i].R+1-k-n-((i-1-pre[i-1])-j));
f[i][j]=((j>0?f[i-1][j-1]*ch1%MOD:0)+f[i-1][j]*ch2%MOD)%MOD;
}
else {
LL ch=max(0,e[i].L+1-j-pre[i-1]);
f[i][j]=f[i-1][j]*ch%MOD;
}
}
if(e[i].id<n)cnt1++;
else cnt2++;
}
LL mval=(k&1?MOD-1:1);
ans=(ans+mval*f[2*n][k]%MOD)%MOD;
}
printf("%lld\n",ans);
return 0;
}
转移中容斥
对于这类容斥,我们发现其通常具有这样的特点:
-
反向情况对原贡献情况的贡献系数为负。
-
反向情况对原不贡献的贡献系数为正。
P14364 [CSP-S 2025] 员工招聘
考虑到我们容易得出 DP 式子 \(f_{i,j}\) 表示目前面试了 \(i\) 人,其中我拒接了 \(j\) 人,排列方案数为多少。考虑转移发现 \(s_i=0\) 的时候一定会被拒,而 \(s_i=1\) 的时候需要分类讨论。
-
\(c>j\):可以录用。
-
\(c\le j\):不能录用。
面试顺序与题目给出顺序无关,直接用 \(sum_i\) 记录 \(c\le i\) 的有多少个,然后在其中容易选出不能录用的。发现我们难以同时决策能录用和不能录用的,因为能录用的总是一段后缀,不能录用的总是一段前缀(按 \(c\) 升序排序),乱选容易出现后效性。
所以我们决定只选 \(c\le j\) 的,我们所需排除的非法情况是:剩下能录用的人中仍满足 \(s_i=1\land c\le j\) 的。定一维 \(k\) 表示钦定有 \(k\) 个被录用但是取了 \(c\le j\) 的人(非法情况),那么每次转移中根据这一维度改变系数:
其中 \(s_i=0\) 的 \(f_{i,j,k}\leftarrow f_{i-1,j-1,k}\) 表示拒绝一个人,暂时不考虑他是谁。
对于 \(s_i=1\),\(f_{i,j,k}\leftarrow f_{i-1,j,k}\) 表示录用一个人,但是同样暂时不考虑他是谁。
\(f_{i,j,k}\leftarrow (sum_{j-1}-(k-1))\times f_{i-1,j-1,k-1}\) 是拒绝一个人,且选定该人为 \(c\le j-1\) 的某个值,体现了反向情况对原不贡献情况的正贡献。
\(f_{i,j,k}\leftarrow -(sum_j-(k-1))\times f_{i-1,j,k-1}\) 是录用一个人,但是他同样是某个 \(c\le j\) 的值,这是容斥的减项,需要排除该反向情况,体现反向情况对原贡献情况的负贡献。
最后答案为 \(\sum_{j=0}^{n-m}\sum_{k=0}^n (n-k)!f_{n,j,k}\),其中 \((n-k)!\) 是我们忽略的位置的任意排列。为什么不需要拒绝和录用的分开来排列?因为我们只钦定 \(c\le j\)。容斥的特性保证了我们只需要限制一些条件,其他条件可以随便乱选,然后最终累加可以得出正确答案。
总结:转移中容斥相比全局容斥来说抽象很多,由于其特性难以直接描述,但是在做的事情其实是把容斥的系数放进了 DP 中,其正确性依然具有保证。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=998244353;
const int N=505;
int n,m,c[N];
char s[N];
LL f[N][N],tmp[N][N],fac[N];
int main(){
//freopen("employ.in","r",stdin);
//freopen("employ.out","w",stdout);
scanf("%d%d",&n,&m);
scanf("%s",s+1);
fac[0]=1;
for(int i=1;i<=n;i++)
fac[i]=fac[i-1]*i%MOD;
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
c[x]++;
}
for(int i=1;i<=n;i++)
c[i]+=c[i-1];
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=i;j++)
for(int k=0;k<=i;k++)
tmp[j][k]=f[j][k],
f[j][k]=0;
if(s[i]=='0'){
for(int j=0;j<=i;j++)
for(int k=0;k<=i;k++)
if(j>0)f[j][k]=tmp[j-1][k];
}
else {
for(int j=0;j<=i;j++)
for(int k=0;k<=i;k++){
f[j][k]=tmp[j][k];
if(k>0)(f[j][k]+=(-(c[j]-(k-1))+MOD)*tmp[j][k-1]%MOD)%=MOD;
if(j>0&&k>0)(f[j][k]+=(c[j-1]-(k-1)+MOD)*tmp[j-1][k-1]%MOD)%=MOD;
}
}
}
LL ans=0;
for(int j=0;j<=n-m;j++)
for(int k=0;k<=n;k++)
(ans+=fac[n-k]*f[j][k]%MOD)%=MOD;
printf("%lld\n",ans);
return 0;
}
P5405 [CTS2019] 氪金手游
手搓限制有向边,发现构成一棵乱七八糟的树,有向边任意定向,不好做。先弱化一下,假定所有限制构成外向树。
首先明确题意,一开始定下所有 \(W_i\),然后 \(u\) 必定比 \(v\) 要先被抽到,令 \(Sum=\sum_{i=1}^n W_i\),\(s_v\) 表示 \(\sum_{v\in tree(u)} W_v\),于是概率:
根据幂级数知识,上式可化简为:
于是只需要边定向决定子树。考虑容斥解决,发现直接树上背包已经达到 \(\Theta(n^2)\),无法再容纳一维容斥系数。于是直接把容斥放在 DP 上面,套用上述提到的容斥系数贡献即可。具体来说:
-
反向情况对原贡献情况的贡献系数为负。
-
反向情况对原不贡献的贡献系数为正。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,bool> PII;
const LL MOD=998244353;
const int N=3e3+5;
int n,val[3][N],siz[N];
LL f[N][N];
vector<PII>G[N];
inline LL qkpow(LL x,LL y){
LL res=1;x%=MOD;
while(y){
if(y&1)res=res*x%MOD;
x=x*x%MOD;
y>>=1;
}
return res;
}
inline LL inv(LL x){return qkpow(x,MOD-2);}
void dfs(int u,int fa){
siz[u]=1;
LL invs=inv(val[0][u]+val[1][u]+val[2][u]);
f[u][1]=1*val[0][u]*invs%MOD;
f[u][2]=2*val[1][u]*invs%MOD;
f[u][3]=3*val[2][u]*invs%MOD;
LL g[N];
for(PII V:G[u]){
int v=V.first;
bool k=V.second;
if(v==fa)continue;
dfs(v,u);
for(int i=1;i<=3*(siz[u]+siz[v]);i++)
g[i]=0;
for(int i=1;i<=3*siz[u];i++){
for(int j=1;j<=3*siz[v];j++){
LL val=f[u][i]*f[v][j]%MOD;
if(k){
g[i+j]=(g[i+j]-val+MOD)%MOD;
(g[i]+=val)%=MOD;
}
else (g[i+j]+=val)%=MOD;
}
}
for(int i=1;i<=3*(siz[u]+siz[v]);i++)
f[u][i]=g[i];
siz[u]+=siz[v];
}
for(int i=1;i<=3*siz[u];i++)
f[u][i]=f[u][i]*inv(i)%MOD;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d%d",&val[0][i],&val[1][i],&val[2][i]);
for(int i=1;i<n;i++){
int u,v;scanf("%d%d",&u,&v);
G[u].emplace_back(make_pair(v,0));
G[v].emplace_back(make_pair(u,1));
}
dfs(1,0);
LL ans=0;
for(int i=1;i<=3*siz[1];i++)
(ans+=f[1][i])%=MOD;
printf("%lld",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号